A 400 pF capacitor, charged by a 100 volt d.c supply is disconnected from the supply and connected to another uncharged 400 pF capacitor. Calculate the loss of energy.

A

10 - 5 J

B

10 - 6 J

C

10 - 7 J

D

10 - 4 J

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Given, capacitor C = 400 × 10 - 12 F and V = 100 V
Initially energy stored = 1 2 C V 2 = 1 2 [ 400 × 10 - 12 × ( 10 2 ) 2 ]
= 1 2 × 4 × 10 - 10 × 10 4 = 2 × 10 - 6 J
⇒ Charge, Q = C V = 4 × 10 - 10 × 100 = 4 × 10 - 8 C
By again connecting the charged capacitor wih an uncharged ideal capacitor.
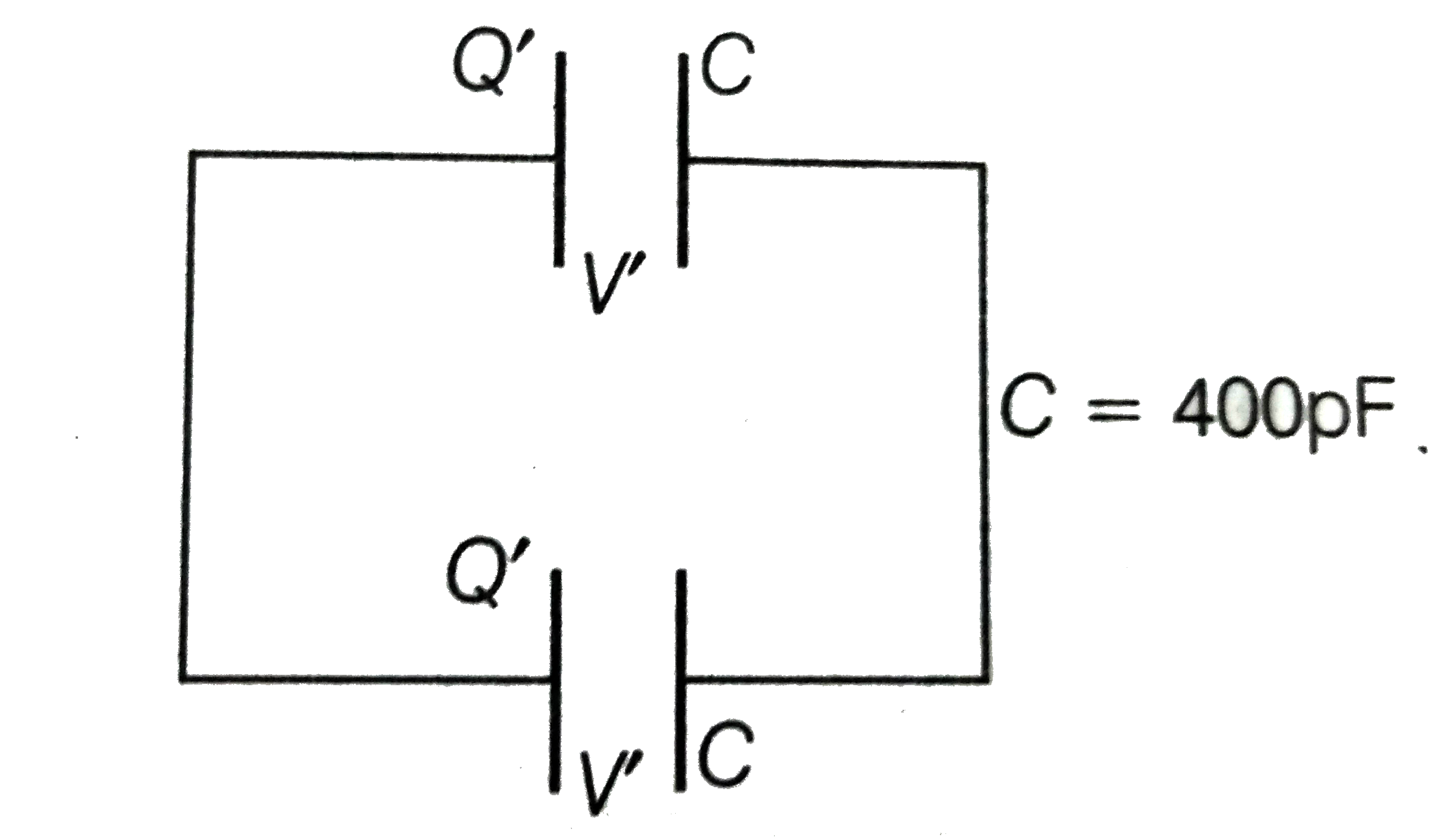
ocr_image
Now, the charge Q will divide into two capacitors.
As V' and C are same for both, Q' will be same for both.
So, Q ′ = Q 2 = 2 × 10 - 8 C
So, energy stored in both the capacitors
= ( ( Q ′ ) 2 2 C ) = ( Q ′ ) 2 2 C
= ( 2 × 10 - 8 ) 2 8 × 10 - 10 = 10 - 6 J
= 0.5 × 10 - 6 J
So, energy lost = 2 × 10 - 6 - 0.5 × 10 - 6
= 1.5 × 10 - 6 J ≈ 10 - 6 J

Updated on:21/07/2023
|
Class 12PHYSICSELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. What is the common potential in V and energy lost in J after reconnection?

    A100,6×10−6
    B200,6×10−5
    C200,5×10−6
    D100,6×10−5

  • A 4μF capacitor is charged by a 200 V supply. It is then disconnected from the supply . And is connected to another uncharged 2μF capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation ?

    AZero
    B5.33×10−2
    C4×10−2
    D2.67×10−2