A resistor of 6kΩwith tolerance 10% and another resistance of 4kΩ with tolerance 10% are connected in series. The tolerance of the combination is about
0.05
0.1
0.12
0.15
The correct Answer is:B
To find the tolerance of the combination of two resistors connected in series, we can follow these steps:
Step 1: Identify the values of the resistors and their tolerances
- Resistor 1 (R1) = 6 kΩ with a tolerance of 10%
- Resistor 2 (R2) = 4 kΩ with a tolerance of 10%
Step 2: Calculate the absolute tolerances for each resistor
- The absolute tolerance (ΔR) for R1 is:
ΔR1=R1×(Tolerance100)=6kΩ×(10100)=0.6kΩ
- The absolute tolerance (ΔR) for R2 is:
ΔR2=R2×(Tolerance100)=4kΩ×(10100)=0.4kΩ
Step 3: Calculate the total resistance of the combination
- The total resistance (R) when resistors are in series is given by:
R=R1+R2=6kΩ+4kΩ=10kΩ
Step 4: Calculate the total tolerance for the combination
- The total tolerance (ΔR) for the combination is the sum of the absolute tolerances:
ΔR=ΔR1+ΔR2=0.6kΩ+0.4kΩ=1kΩ
Step 5: Calculate the tolerance of the combination
- The tolerance of the combination can be expressed as a percentage of the total resistance:
Tolerance of combination=ΔRR×100=1kΩ10kΩ×100=10%
Final Answer
The tolerance of the combination is approximately 10%.
---
- Resistor 1 (R1) = 6 kΩ with a tolerance of 10%
- Resistor 2 (R2) = 4 kΩ with a tolerance of 10%
- The absolute tolerance (ΔR) for R1 is:
ΔR1=R1×(Tolerance100)=6kΩ×(10100)=0.6kΩ
ΔR2=R2×(Tolerance100)=4kΩ×(10100)=0.4kΩ
- The total resistance (R) when resistors are in series is given by:
R=R1+R2=6kΩ+4kΩ=10kΩ
- The total tolerance (ΔR) for the combination is the sum of the absolute tolerances:
ΔR=ΔR1+ΔR2=0.6kΩ+0.4kΩ=1kΩ
- The tolerance of the combination can be expressed as a percentage of the total resistance:
Tolerance of combination=ΔRR×100=1kΩ10kΩ×100=10%
The tolerance of the combination is approximately 10%.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE 226videos
CURRENT ELECTRICITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - MHT CET CORNER32videos
CURRENT ELECTRICITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - MHT CET CORNER32videos
CURRENT ELECTRICITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - COMMUNICATION SYSTEMEXERCISE - MHC CET Corner6videos
COMMUNICATION SYSTEM
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELASTICITY EXERCISE - MHT CET CORNER16videos
ELASTICITY
Similar Questions
Knowledge Check
- Question 1 - Select One
A resistor of 10kΩ has a tolerance of 10% and another resistor of 20kΩ has a tolerance of 20%. The tolerance of the series combination is rearly
A10%B20%C15%D17% - Question 2 - Select One
If 400Ω of resistance is made by adding four 100Ω resistance of tolerance 5%, then the tolereance of the combinations
A5%B10%C15%D20% - Question 3 - Select One
A wire of resistance 1 Ω is elongated by 10%. The resistance of the elongated wire is
A1.1ΩB11.1ΩC1.21ΩD12.1Ω
How will you repersent a resistance of 3700Ω±10% by colour code?
View SolutionThe length of the resistance wire is increased by 10%. What is the corresponding change in the resistance of wire
View SolutionA constant voltage dc source is connected, as shown in Fig. A2.7, across two resistors of resistances 400kΩ and 100kΩ. What is the reading of the voltmeter, also of resistance 100kΩ, when connected across the second resistor as shown?
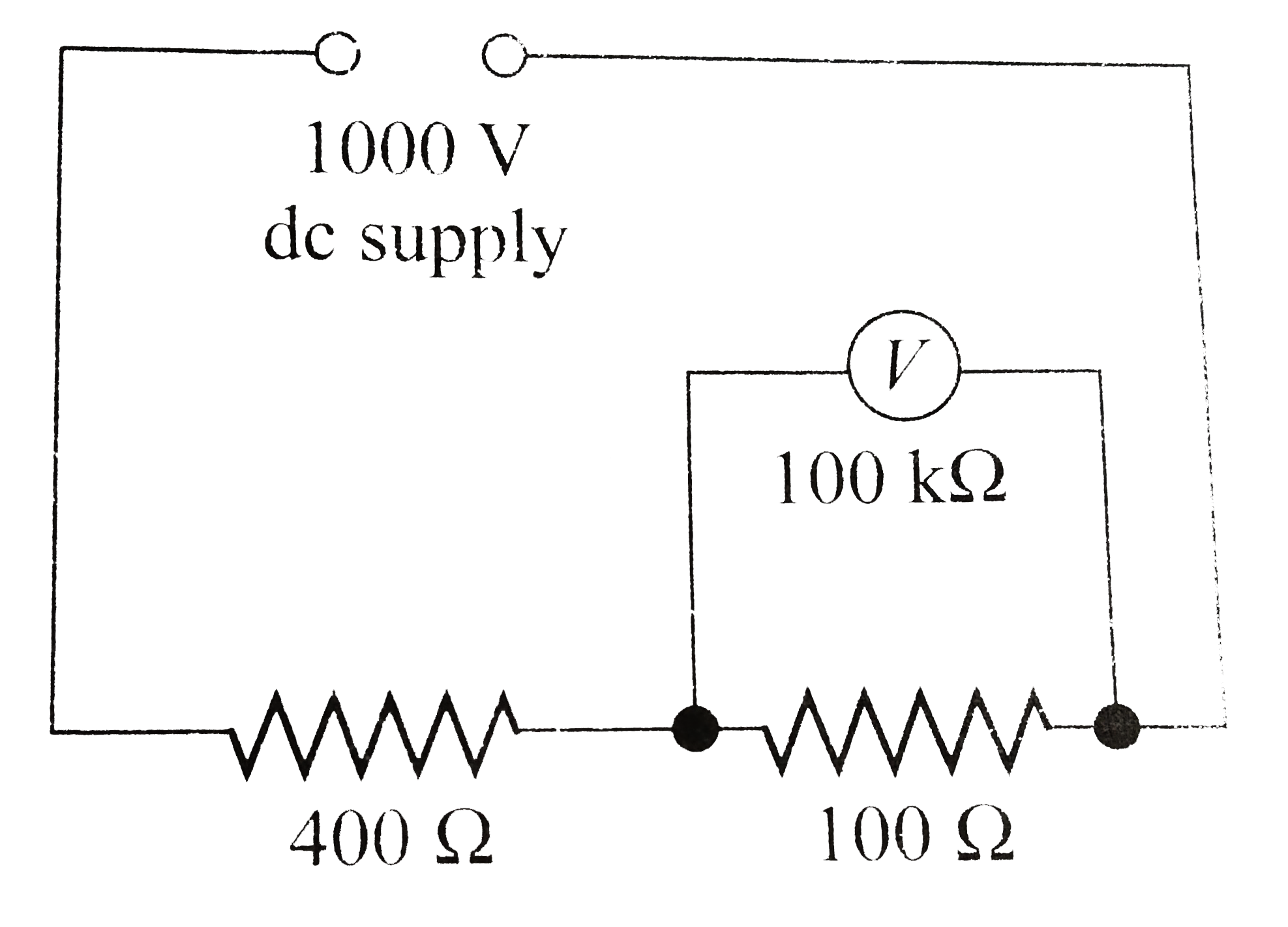 View Solution
View SolutionThe resistance of a wire is 10Ω. Its lengthis incrased by 10% by stretching. The new resistance will now be
View SolutionA wire of resistance R is stretched so that its length increases by 10%. The resistance of the wire increases by
View Solution

