A log of wood of length l and mass M is floating on the surface of a river perpendicular to the banks. One end of the log touches the banks. A man of mass m standing at the other end walks towards the bank. Calculate the displacement of the log when he reaches nearer end of the log

Text Solution
Verified by Experts

Let PQ be the log of wood. As there is no external force, the centre of mass of man and the log system remains at rest. Let the bank of the river be the origin A. Initially, the man is at point Q.
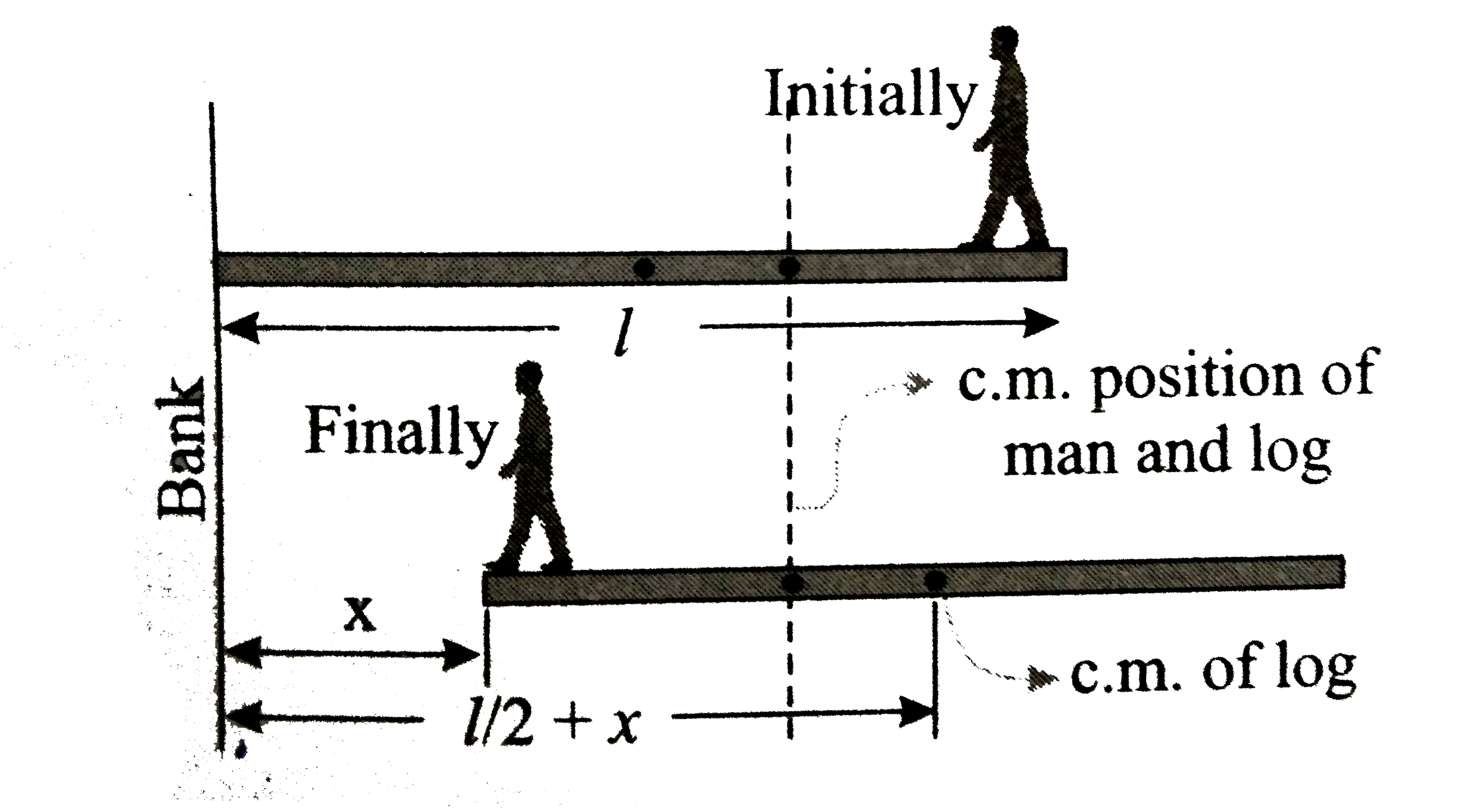
ocr_image
Let m=mass of man
M=mass of log
x=displacement of log w.r.t ground (here water)
XCM (initial) =m(l)+m(l2)m+M
XCM(final)=m(x)+M(l/2+x)m+M
Now XCM(initial) =XCM (final)
⇒ml+Ml2=mx+Ml2+Mx
⇒x=mlm+M
Hence the log moves away from the bank through a distance of ml(m+M)
Alternative method: Displacement of the log =△x1=x
Displacement of the man =△x2=l−x
Apply m1x1=m2x2⇒(if the centre of mass remains at the same place)
⇒Mx=m(l−x)⇒xml(m+M)

Doubtnut Promotions Banner
|
Class 11PHYSICSCENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A boy of mass m is standing at one end of a boat of mass M and length l. The boy walks to the other end, the displacement of the

    ACM is zero
    Bboat is mlM+m
    Cboy is mlM+m
    Dboat is mMl

  • A boat of length 10m and mass 450kg is floating without motion in still water. A man of mass 50kg standing at one end of it walks to the other end of it and stops. The magnitude of the displacement of the boat in metres relative to ground is

    A(a) zero
    B(b) 1m
    C(c) 2m
    D(d) 5m

  • A 500 kg boat is 9 m long and is floating without motion on still water. A man of mass 100 kg is at one end and if he runs to the other end of the boat and stops, the displacement of the boat is

    A1.5 m in the direction of displacement the man
    B0.755 m in the direction of displacement the man
    C1.5 m in the direction opposite to the displacement the man
    D0.75 m in the direction opposite to the displacement the man