Let there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle $A$ starts with a velocity $v_{1}$ towards line $A B$ , particle $B$ starts with the velocity $v_{2}$ , towards line $B C$ and particle $C$ starts with velocity $v_{3}$ towards line $C A$ . Find the displacement of the centre of mass of the three particles $A, B$ and $C$ after time $t$ . What would it be if $v_{1} = v_{2} = v_{3}$ ?

Video Solution

Text Solution

Verified by Experts

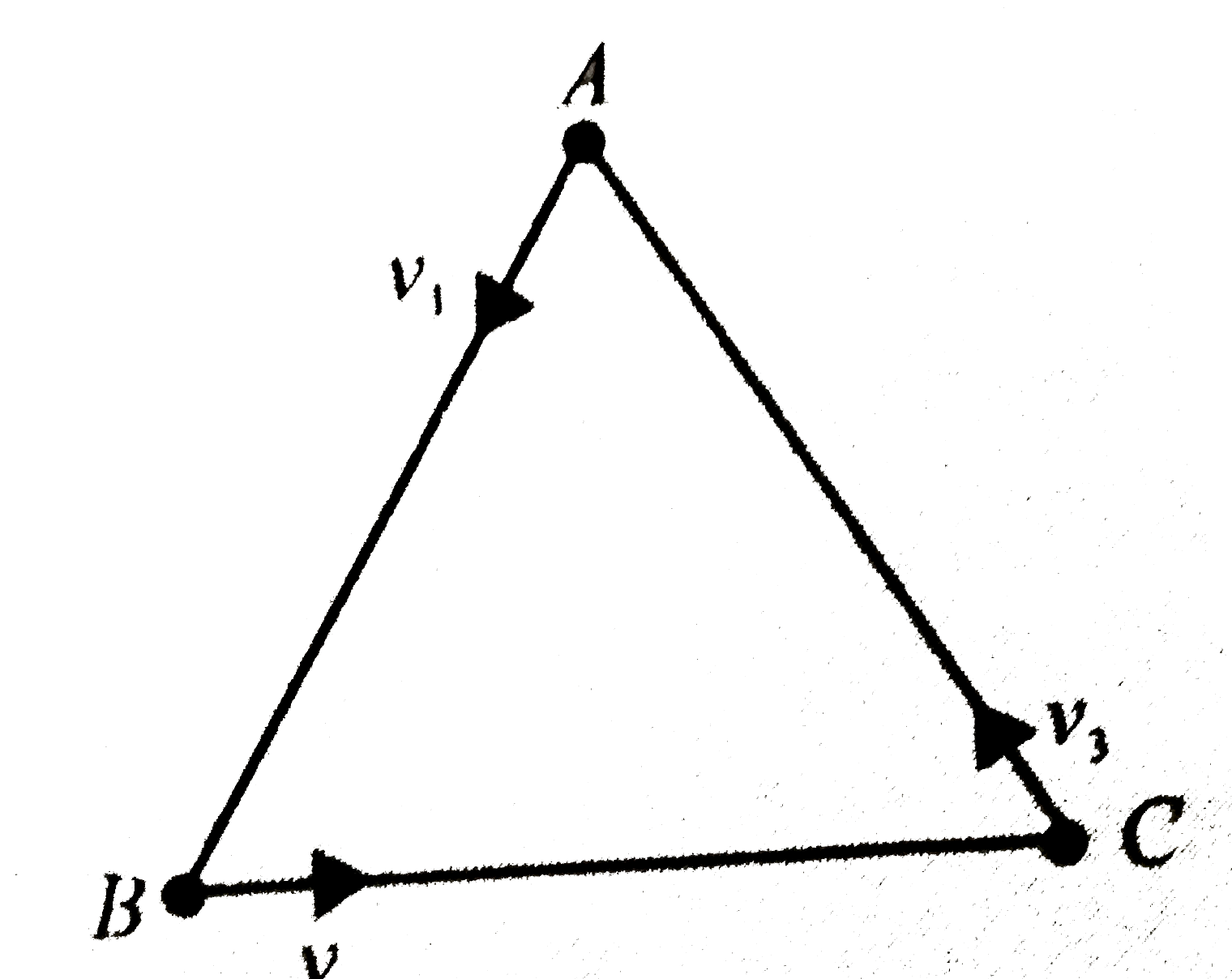
First we write the three velocities in vectorial form, taking right direction as positive $x$ -axis and upwards as positive $y$ -axis.
$\to - - - (1) = - \frac{1}{2} v_{1} ˆ i - \frac{\sqrt{3}}{2} v_{1} ˆ j$
${\to v}_{2} = v_{2} ˆ i, {\to v}_{3} = \frac{1}{2} v_{3} ˆ i + \frac{\sqrt{3}}{2} v_{3} ˆ j$
Thus the velocity of centre of mass of the system is
${\to v}_{C M} = \frac{{\to v}_{1} + {\to v}_{2} + {\to v}_{3}}{3}$
$= (v_{2} - \frac{1}{2} v_{1} - \frac{1}{2} v_{3}) ˆ i + \frac{\sqrt{3}}{2} (v_{3} - v_{1}) ˆ j$ which can be written as ${\to v}_{C M} = v_{x} ˆ i + v_{y} ˆ j$
Thus displacement of the centre of mass in time $t$ is $△ \to r = v_{x} t ˆ i + v_{y} t ˆ j$
If $v_{1} = v_{2} = v_{3} = v$ we have
${\to v}_{C M} = 0$
Therefore there is no displacement of centre of mass of the system.

Updated on:21/07/2023

Three particles of equal masses are placed at the corners of an equilateral triangle as shown in the figure. Now particle $A$ starts with a velocity $v_{1}$ towards line $A B$ , particle $B$ starts with a velocity $v_{2}$ towards line $B C$ and particle $C$ starts with velocity $v_{3}$ towards line $C A$ . The displacement of $C M$ of three particle $A, B$ and $C$ after time $t$ will be (given if $v_{1} = v_{2} = v_{3})$

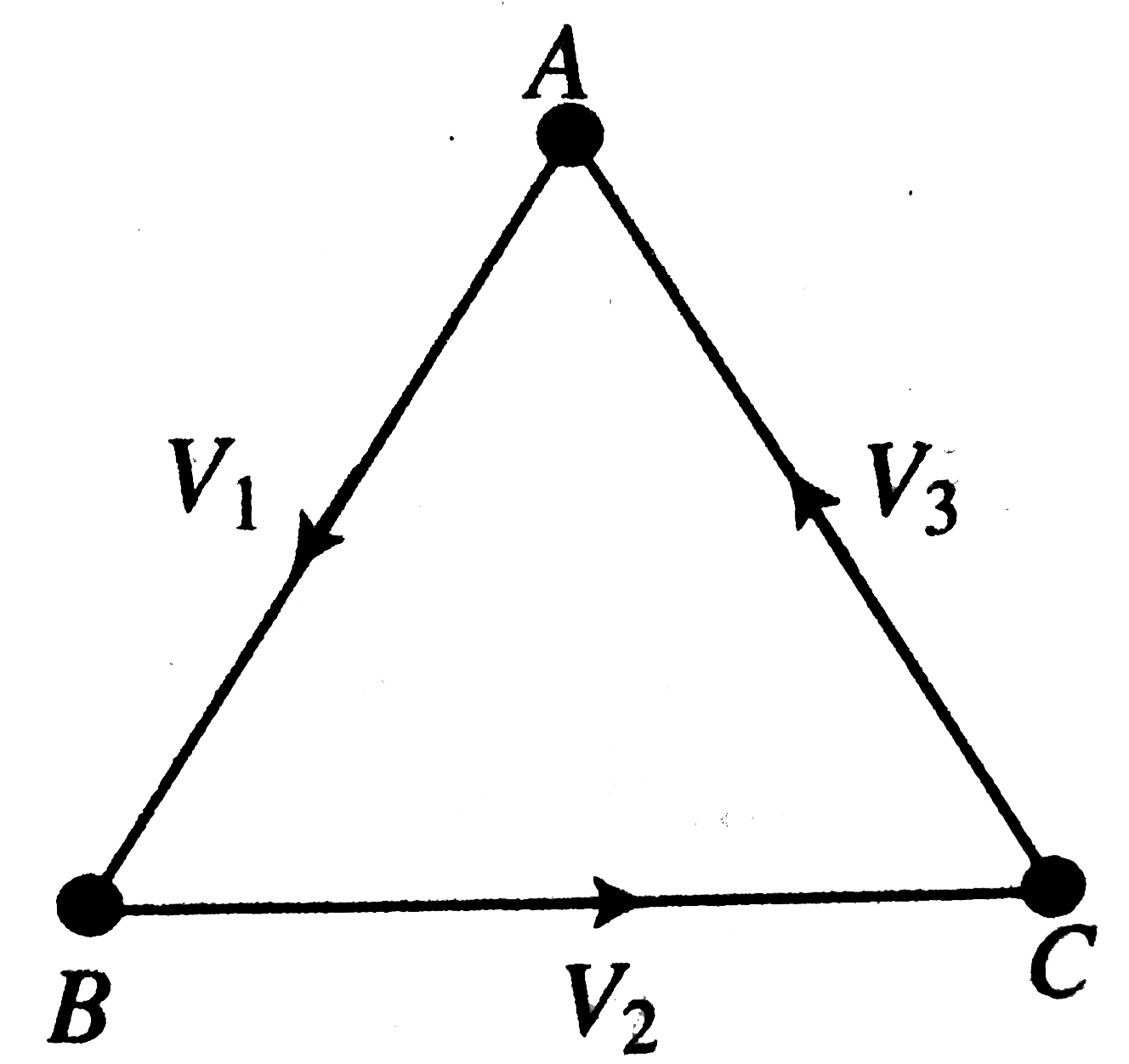Azero
B $\frac{v_{1} + v_{2} + v_{3}}{3} t$
C $\frac{v_{1} + \frac{\sqrt{3}}{2} v_{2} + \frac{v_{3}}{2}}{3} t$
D $\frac{v_{1} + v_{2} + v_{3}}{4} t$
Three particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of

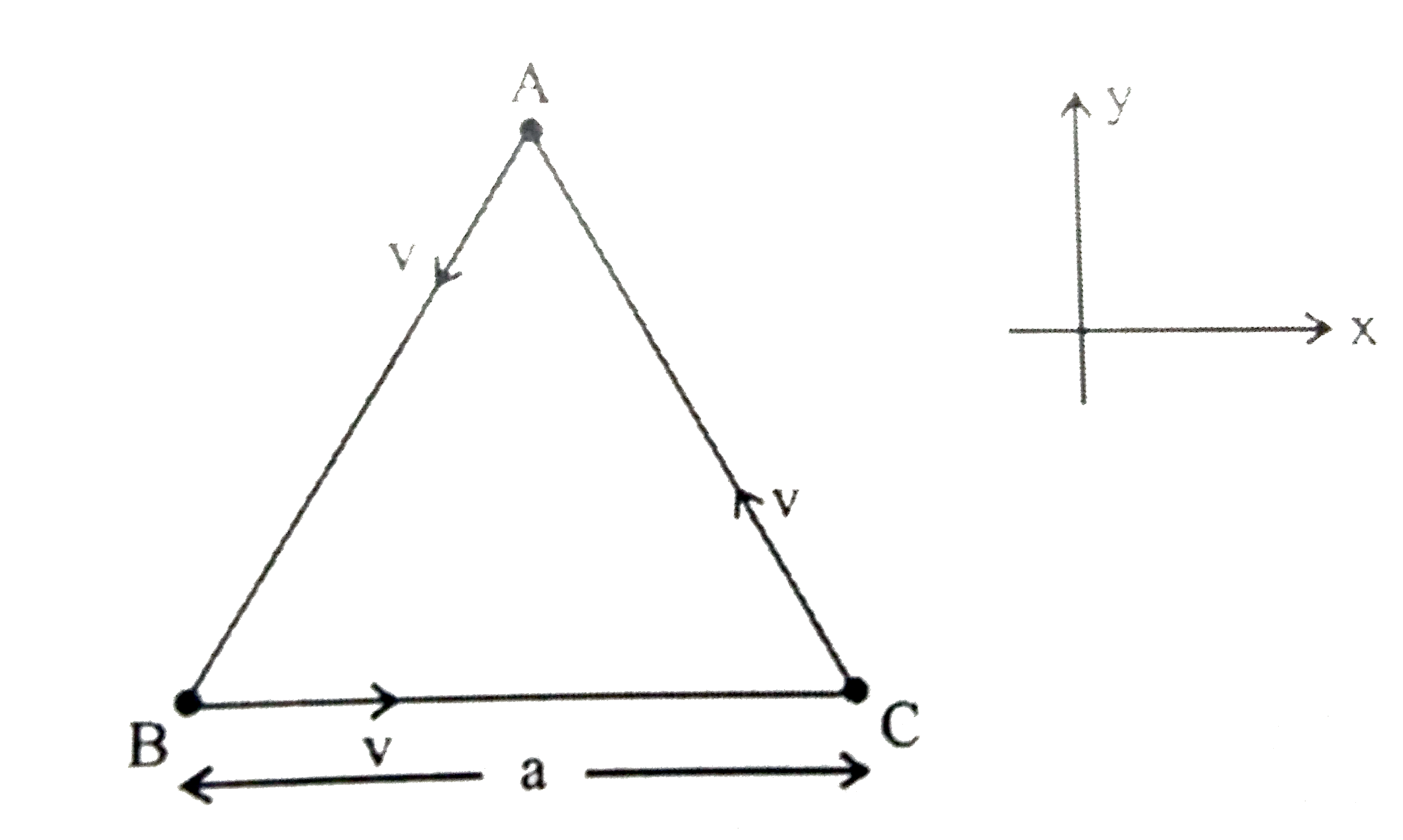A $A w r t . B is = \frac{v {cos 30}^{\circ}}{a} in z-direction$
B $B w r t . C is = \frac{v {cos 30}^{\circ}}{a} in z-direction$
C $A w r t . C is = \frac{v {cos 30}^{\circ}}{a} in z-direction$
D $B w r t . A is = \frac{v {cos 30}^{\circ}}{a} in z-direction$
Two identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
Av
B $v / 3$
C $v / 2$
Dzero