A ball of mass collides with a stationary wedge of mass , perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is , calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

The correct Answer is:
Let velocity of wedge after colision be and that of ball be . We can show that , because otherwise final would be greater than initial which is not possible will be perpendicular to wedge surface.
From Newoton's experimental law:
.....i

Conservastion of linear mometum along -axis.
...........ii
From i and ii
Put the value of in eqn i to get
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
An object initially at rest explodes into three fragments A,B and C. The momentum of A is pˆi and that of B is √3pˆj
where p is a+ve number. The momentum of C will be
View SolutionA ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
View SolutionA ball is dropped on a floor from a height h. If the coefficient of restitution is e, find the height to which the ball will rise after touching the floor and the time it will take to come to rest again.
View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionA ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?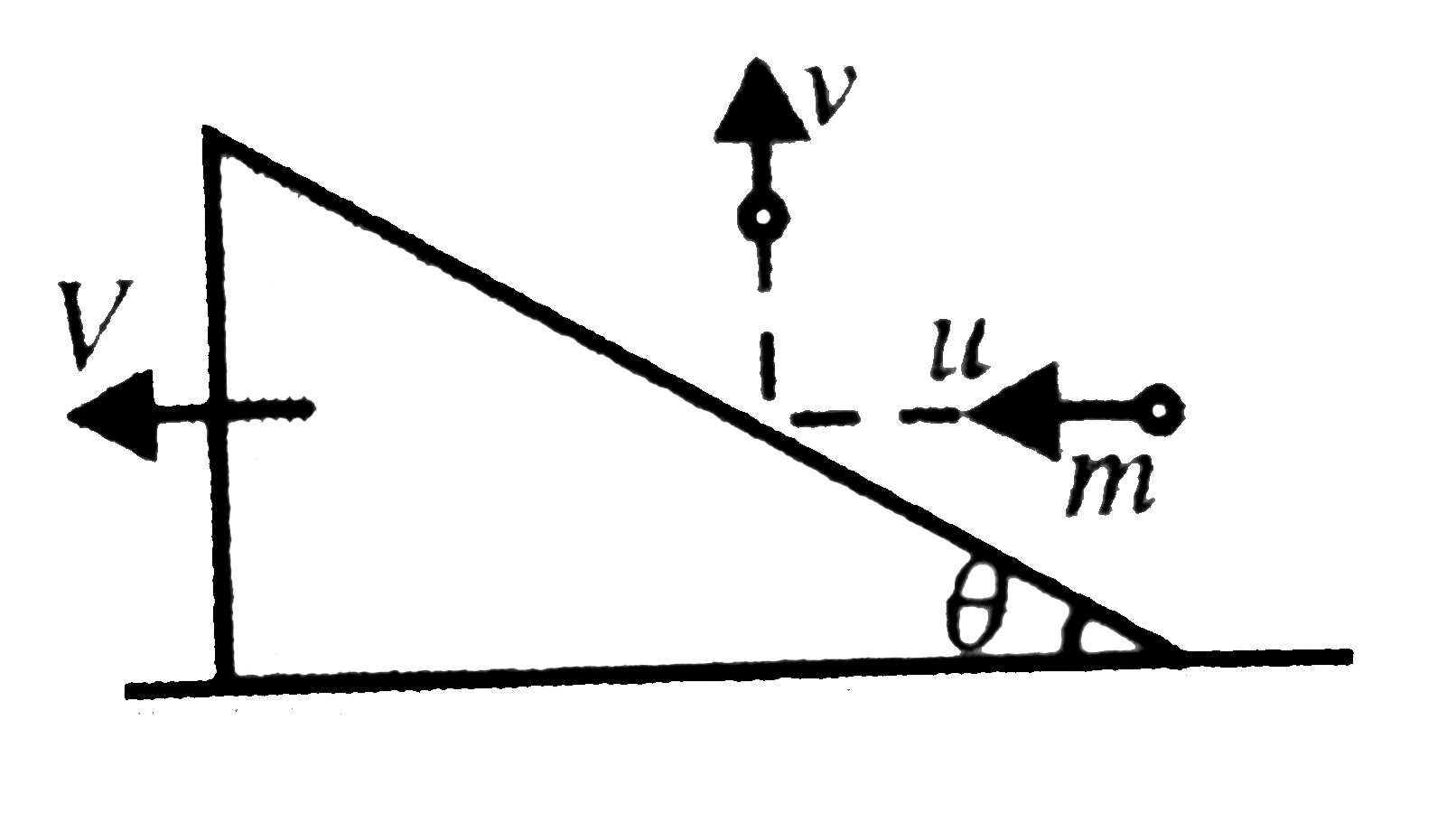
View SolutionA wedge of mass M is kept at rest on smooth surface a particle of mass m hits the wedge normally. Find the velocity of wedge and particle just after collision. Take coefficient of restitution as e .
View SolutionA ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface. a. Calculate the velocity of wedge immediately after collision. b. Calculate the maximum height the ball can ascend on the wedge.
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionA ball of mass m moving with velocity u strikes another identical ball at rest. Find the velocities of the balls after the collision if the coefficient of restitution is e and the collision is head -on. Also , calculate the loss in K.E.
View SolutionA wedge mass m rest on horizontal surface. The inclination of the wedge is α. A ball of mass m moving horizontal with speed u hits the inclined face of the wedge in elastically and after hitting slides up the inclined face of the wedge. Find the velocity of the wedge just after collision. Neglect any friction.
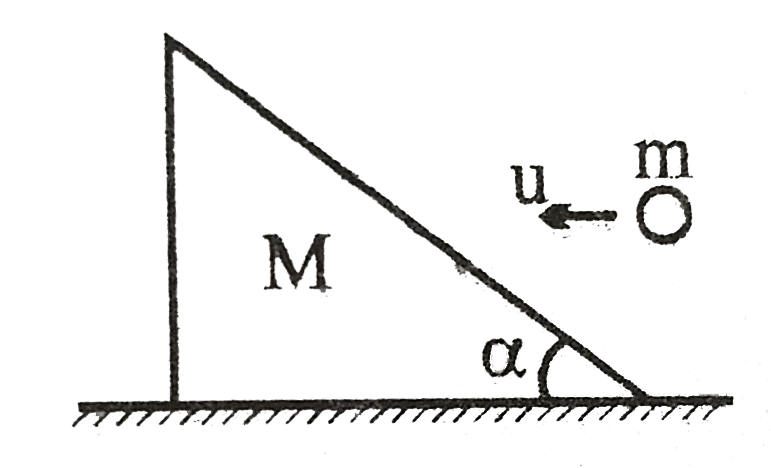
View Solutionshow a smooth spherical ball of mass m striking two identical equilateral triangular wedges of mass M. At the instant of impact velocity of the ball is υ0. Taking coefficient of restitution e, determine the velcities of the sphere and the wedges just after collision.

View SolutionA ball of mass m moving vertically down , collides with inclined surface of the wedge . After the collision , wedge starts moving in horizontal direction with velocity v0 . If all the surfaces are smooth then impulse applied by wedge on the ball during collision is given by

View SolutionA particle of mass m moving horizontal with v_(0) strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h. The final velocity of the wedge v_(2) is
View SolutionA smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle theta with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View Solution
