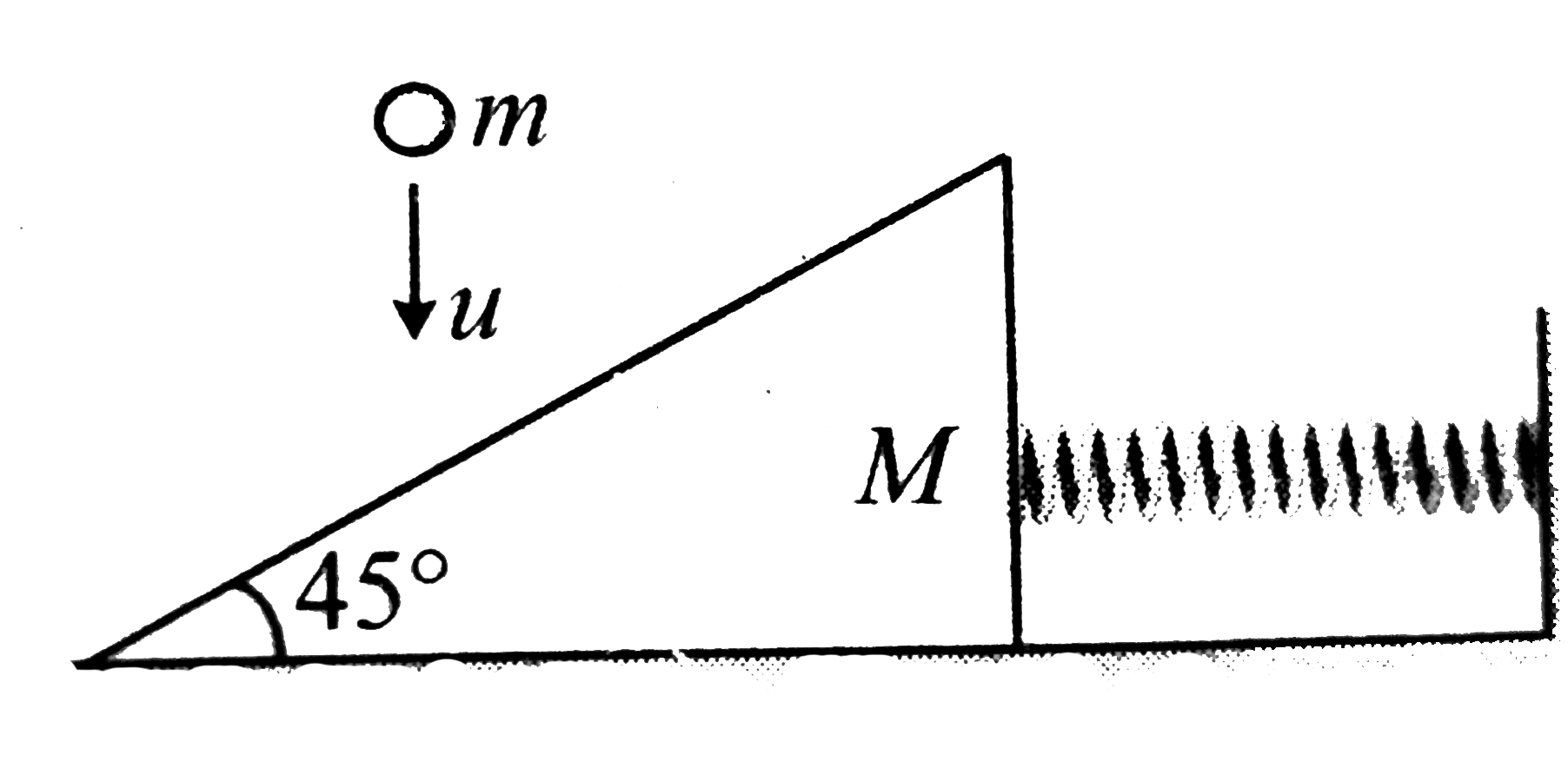
A ball of mass m hits a wedge of mass M vertically with speed u, which is placed, on a smooth horizontal surface. Find the maximum compression in the spring, if the collision is perfectly elastic and no friction any where. Spring constant of spring is K.
The correct Answer is:√MK
Let after collision, the ball has velocity v1 and wedge v2 as shown.
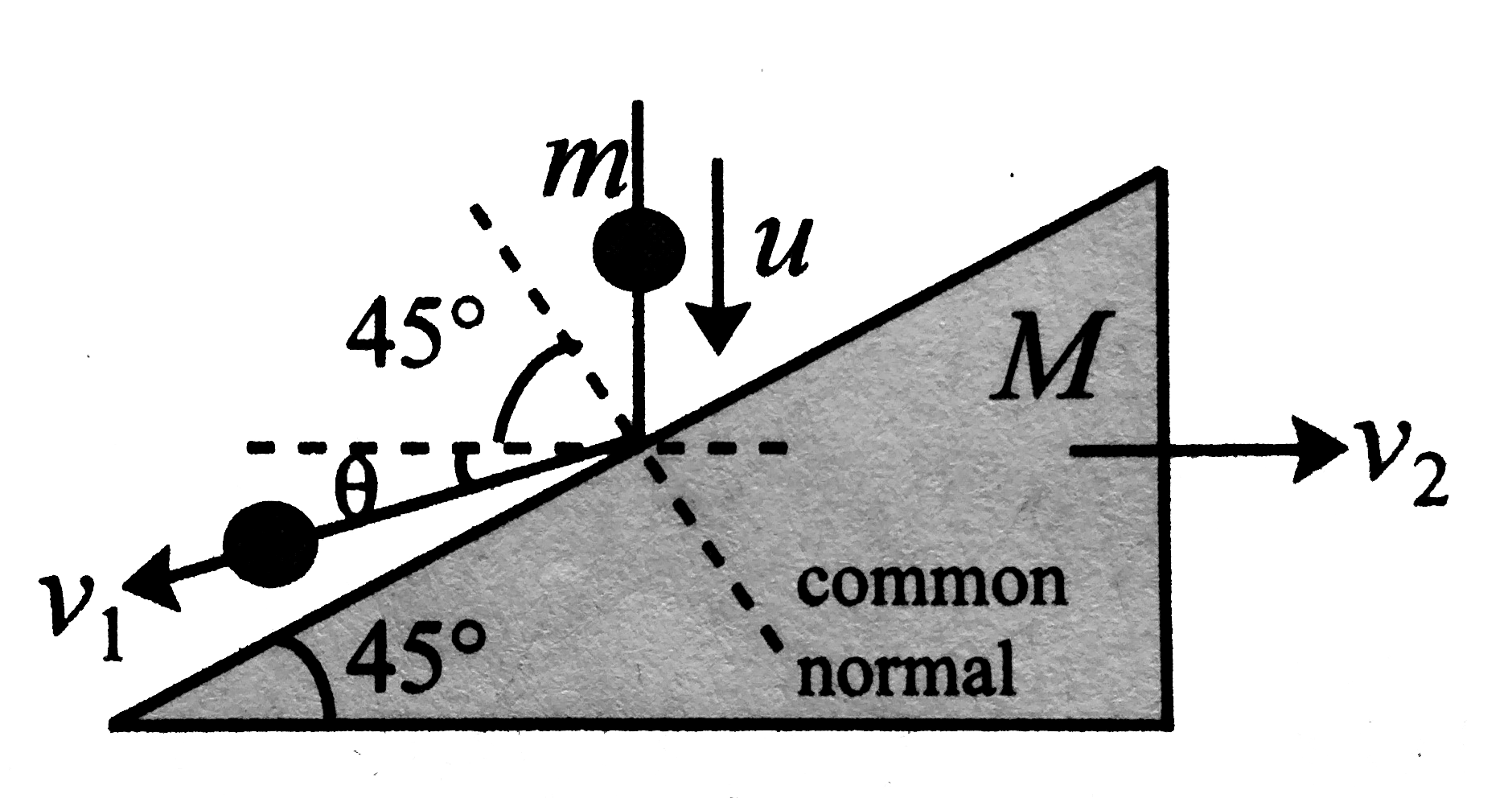
Aplying conservation of momentum in horizontal direction
mv1cosθ=Mv2 ……….i
From Newton's experimental law:
e=1=v2sin45∘−[−v1cos(45+θ)]ucos45∘
⇒u=v2+v1cosθ−v1θ ...........ii
Velocity component of the ball along the surfasce of wedge will remain the same as during collision there is no force on the ball in this direction So
usin45∘=v1cos(45−θ)⇒u=v1cosθ+v1sinθ...iii
From i and ii and iii
v2=2mum+2M
To find maximum compression in the sprig, after collision apply conservation of energy for the system of wedge and spring.
12Mv22=12Kx2
⇒x=√Mxv2⇒x(2mum+2M)√MK
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
In the fig 4.24 a block of mass m moves with velocity v0 toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
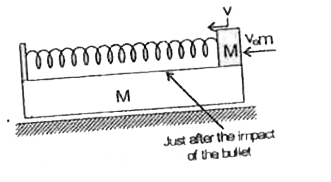
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A bullet of mass 'm' is fired from a gum of mass M with a (muzzle) velocity u. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find maximum compression of spring of spring constant (K) isA√MK(mucosθm)B√KM(MucosθM+m)C√MK(mucosθM+m)D√MK(mucosθM)
In the figure shown, initially the spring is in relaxed position. A bullet of mass m hits the block 'A' with horizontal speed v0 and gets embedded into it. Find the maximum compression in the spring. Stiffness of the spring is K. Neglect any friction and deformation in the spring during collision.
View SolutionIn the figure shown, initially the spring is in relaxed position. A bullet of mass m hits the block 'A' with horizontal speed v0 and gets embedded into it. Find the maximum compression in the spring. Stiffness of the spring is K. Neglect any friction and deformation in the spring during collision.

View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.

View SolutionA small mass 'm' is sliding down on a smooth curved incline form a height 'h' and finally moves through a horizontal smooth surface. A light spring of force constant K is fixed with a vertical rigid stand on the horizontal surface, as shown in the figure. Find the value for the maximum compression in the spring if mass 'm' is released from rest from height 'h' and hits the spring in the horizontal surface.
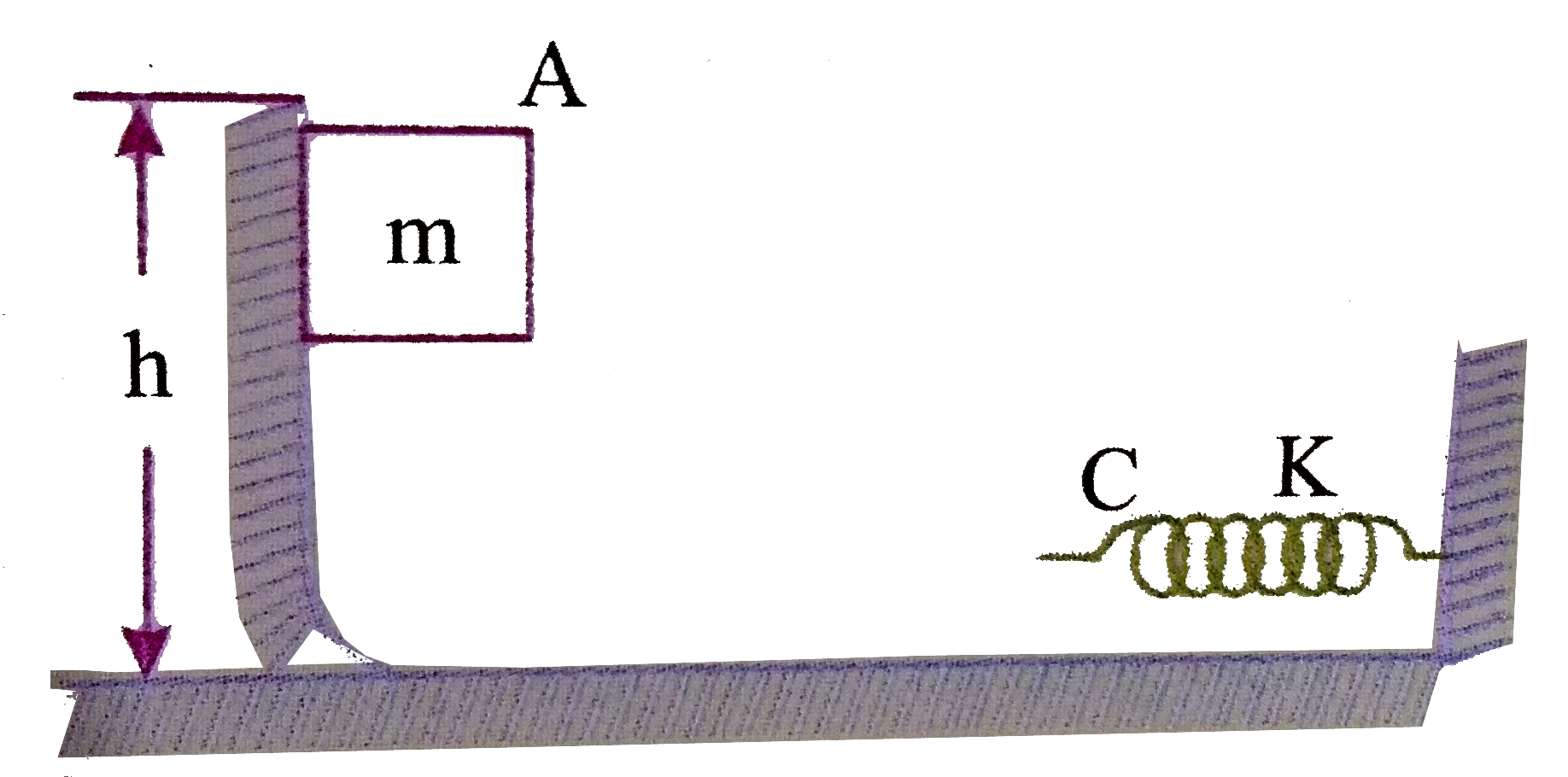 .
.
View Solution
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
