A rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.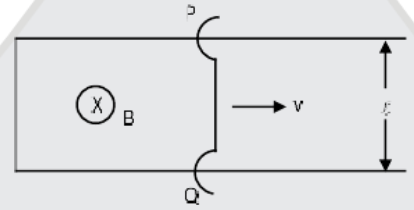
(12)(BvlR)
(2BvlR)
(3BvlR)
(BvlR)
The correct Answer is:D
Step by step video, text & image solution for A rod having length l and resistance R is moving with velocity v on a pi shape conductor. Find the current in the rod. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig a rod of length l and mass m moves with an intial velocity u on a fixed frame containing inductor L and resistance R.PQ and MN are smooth conducting wires. There is auniform magnetic field of strength B. Initially, there is no current in the inductor. find the total cherge flows through the inductor by the time, velocity of rod becomes νf and the rod has travelled a distance x.

View SolutionA rod of length l is moving velocity v "in magnetic field" b as seen in . Find the emf induced in all three cases.
(a)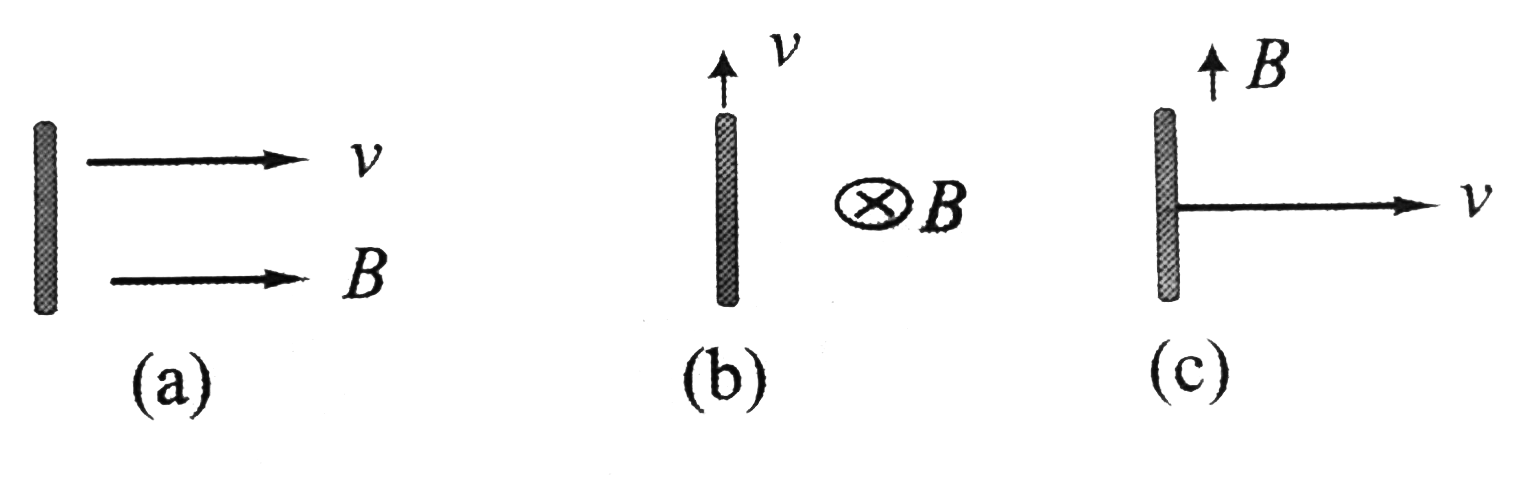
View Solution
Knowledge Check
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
ABlvRBBlvCzeroDB2v2l2RA frame a bed and a sliding rod PQ of resistance R, start moving with the velocities v and 2v respectively parallel to a long wire carrying steady current I, as shown in the figure.
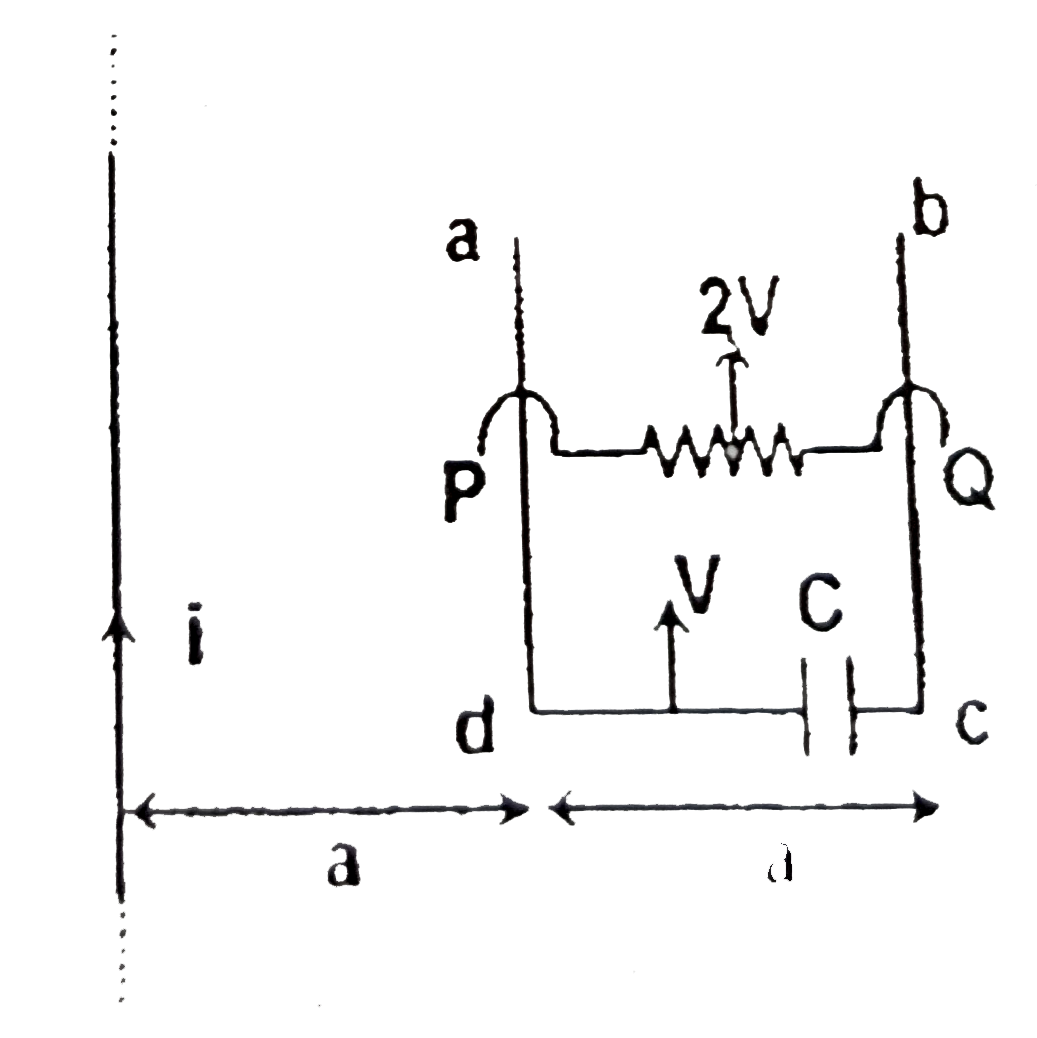 Acharge on the capacitor at time t is q=Cμ0ivln22π[1−e−t/RC]Bcharge on the capacitor at time t is q=Cμ0ivln2π[1−e−t/RC]Ccurrent passing through the resistor at time t is i=μ0ivln22πR[e−t/RC]Dcurrent passing through the capcitor at time t is i=μ0ivln2πR[e−t/RC]
Acharge on the capacitor at time t is q=Cμ0ivln22π[1−e−t/RC]Bcharge on the capacitor at time t is q=Cμ0ivln2π[1−e−t/RC]Ccurrent passing through the resistor at time t is i=μ0ivln22πR[e−t/RC]Dcurrent passing through the capcitor at time t is i=μ0ivln2πR[e−t/RC]A cylindrical copper rod has length L and resistance R. If it is melted and formed into another rod of length 2L, the resistance will be
ARB2RC4RD8R
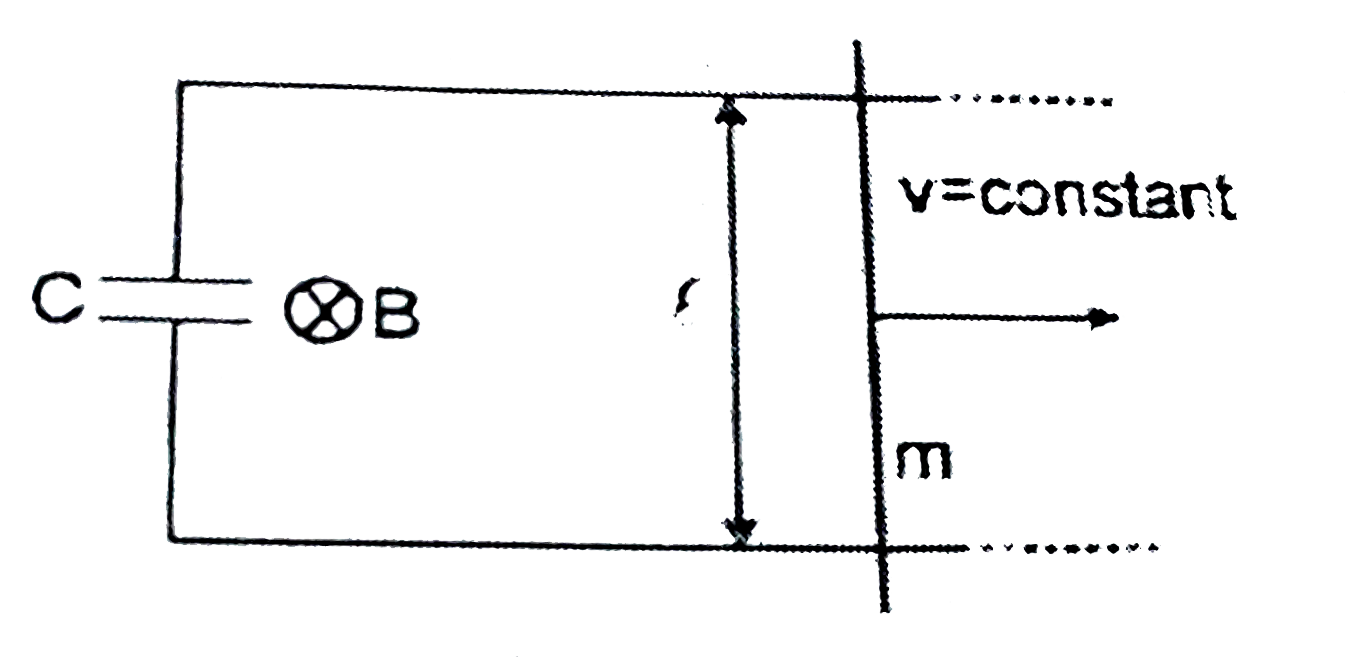
In the figure shown a conducting rod of length l, resistance R and mass m is moved with a constant velocity v. The magnitude field B varies with time t as B=5t, what t is time in second. At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged. the rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance. Find the current in the circuit as a function of time t.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
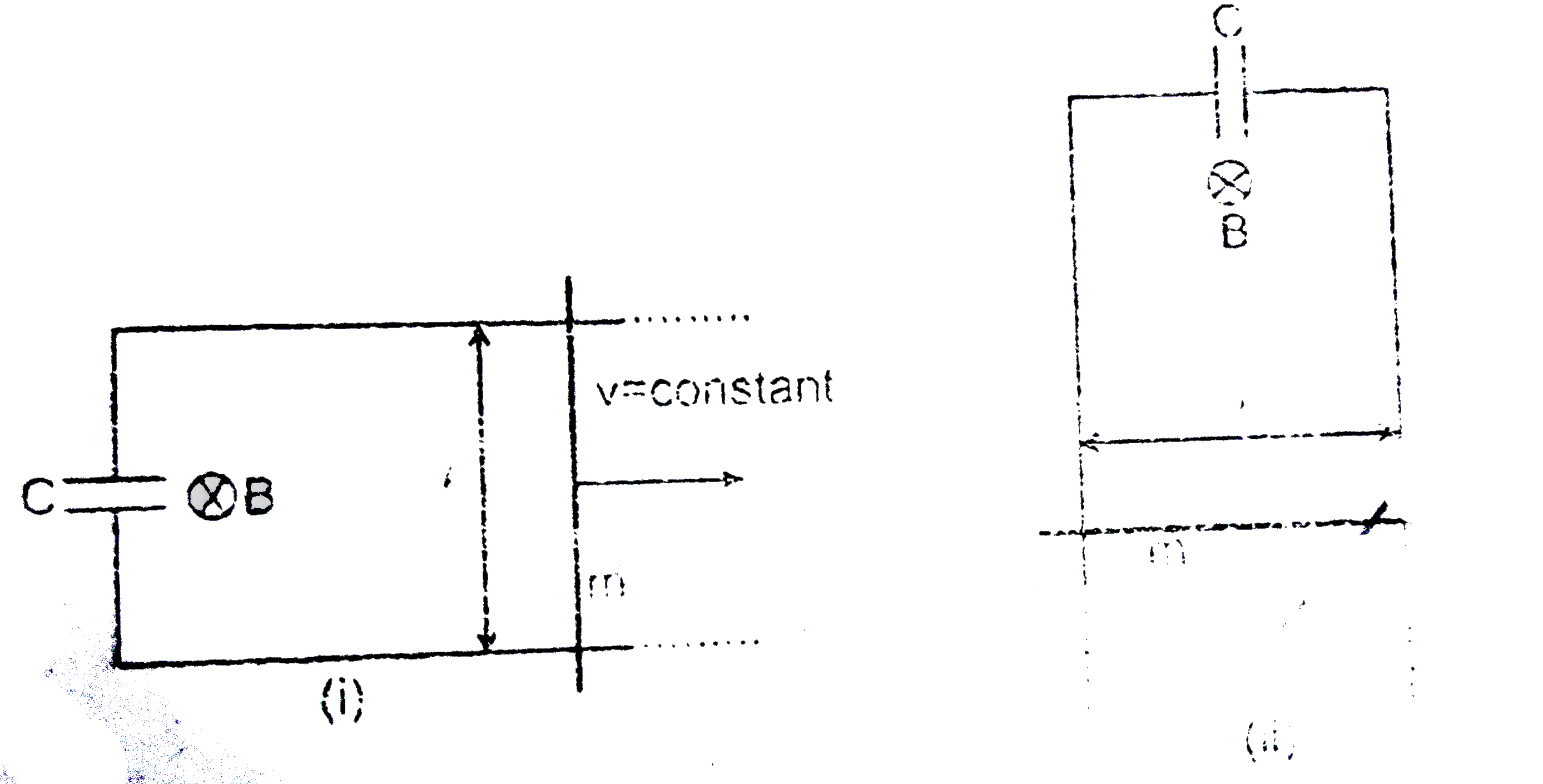
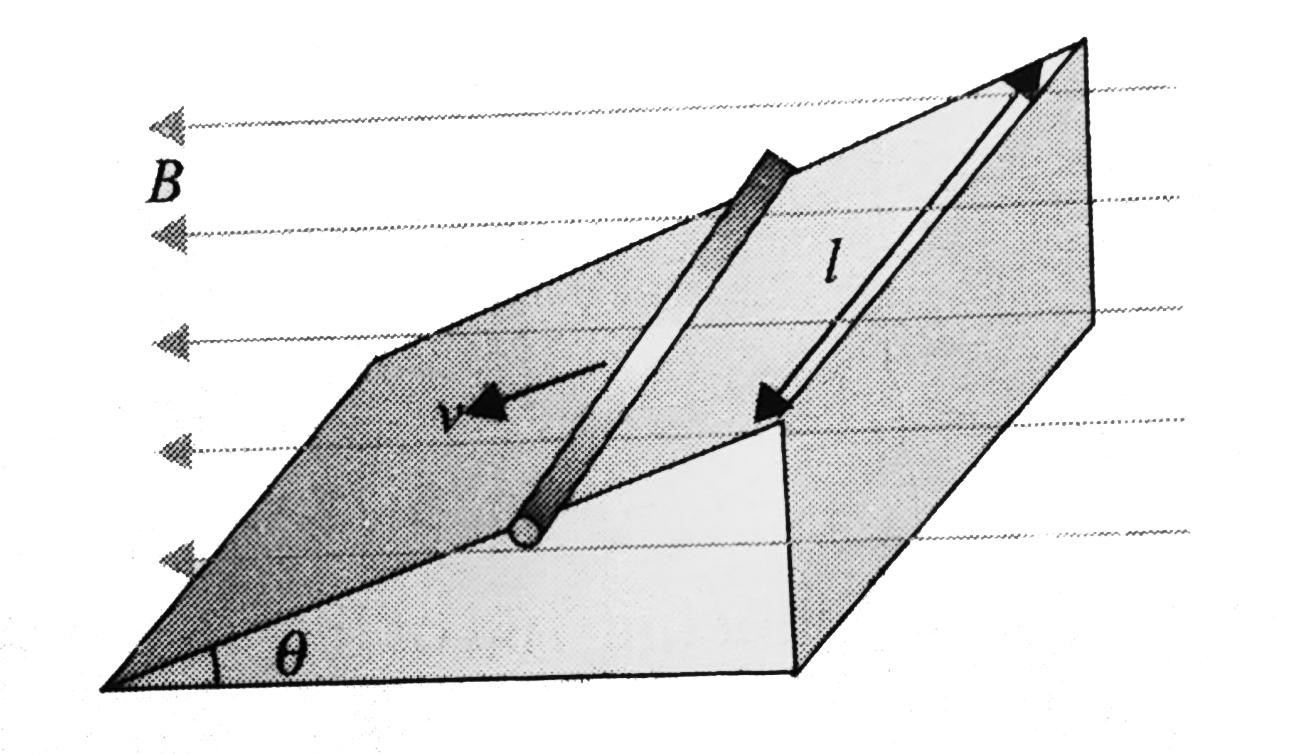
View SolutionA rod of mass m, length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v. If a uniform horizontal magnetic field B exists, then find thevalue of B.
View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
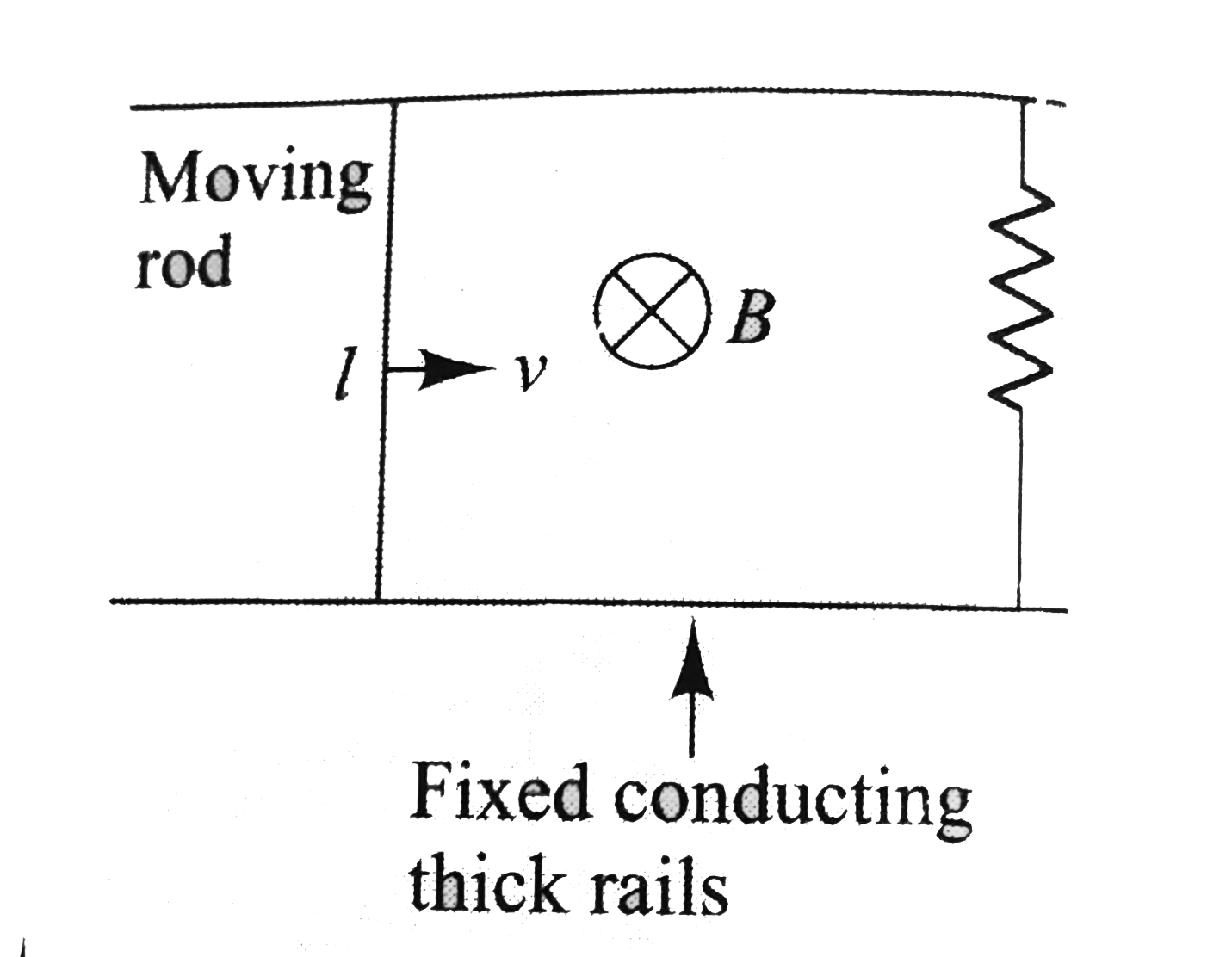
View Solution
