In figure calculate the linear acceleration of the blocks.
Mass of block B=8kg
mass of disc shaped pulley =2kg (take g=10m/s2)
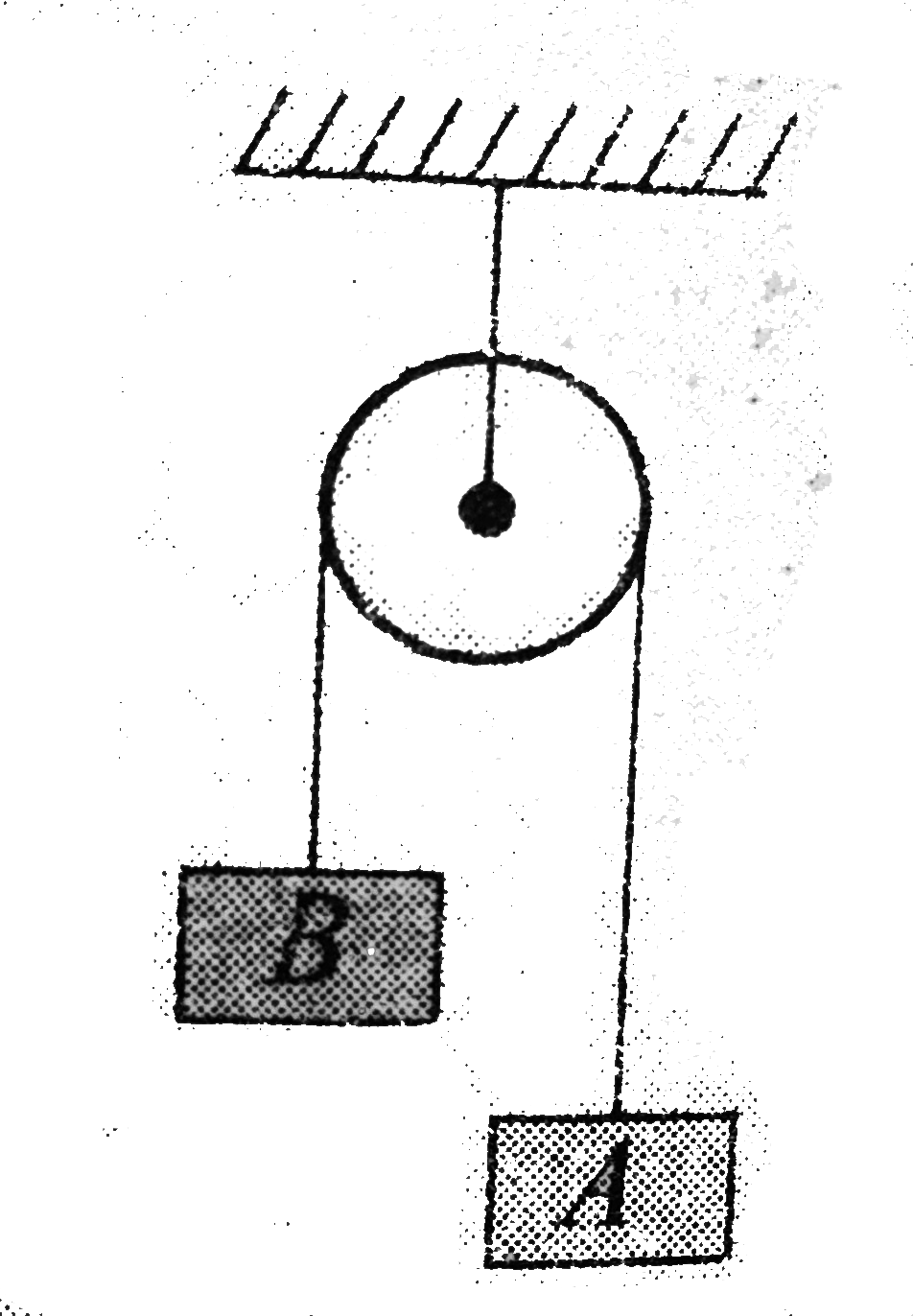
Let R on the radius of the pulley and T1 and T2 be the tension in the left and right portions of the string Unlike laws of motion where tension in striln is the same on both the sides of the pulley. In this case, the string does not slide and the pulley rotates. the tensions on both the sides of the pulley will be different. this This different tensions will provide angular acceleration to pulley.
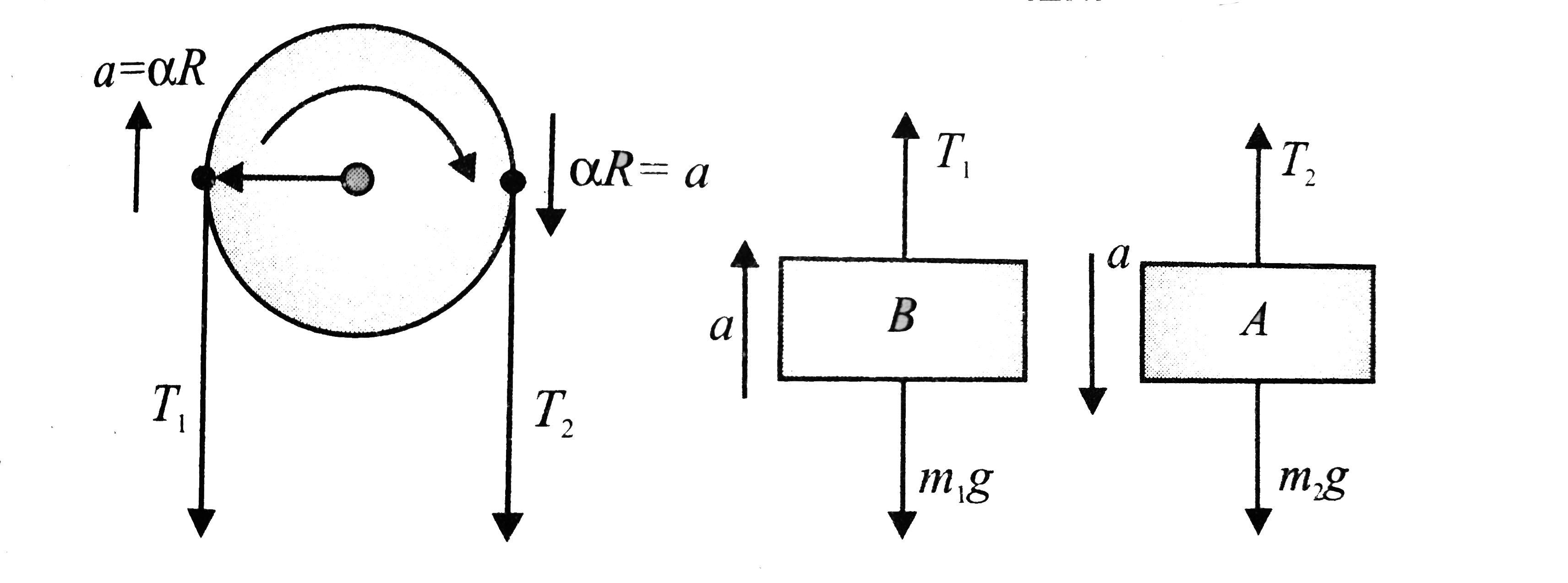
Let m1=8kg,m2=10kg,M=2kg
Let a be the acceleration of blocks.
for the blocks (linear motion)
T1−m1g=m1a.......i
m2g−T2=m2a...........ii
For the pulley (rotation)
Net torque τ≠t=Iα
T1R−T1R=12MR2α
The linear acceleration of the blocks is the same as the tangetial acceleration of any point on the circumference of the pulley which is Rα.
a=Rα
Dividing eqn iii by R and addinng to eqn i and ii we get
m2g−m1g=m2a+m1a+M2Rα⇒m2g−m1g
=(m2=m1+M2)a
a=m2−m1m2+m1+M2g=(10−8)g10+8+22=2019m/s2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
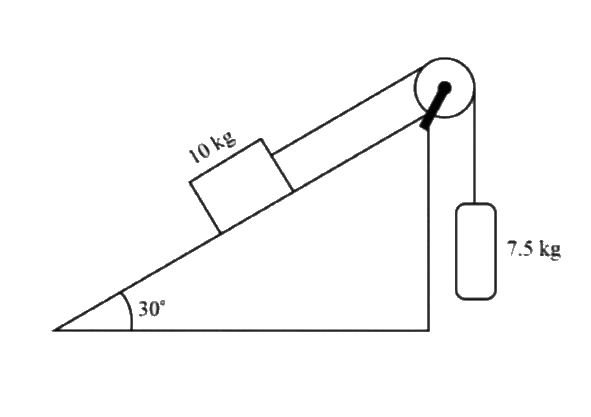
The acceleration of the 10 kg mass block shown in the figure is : -
 View Solution
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View SolutionFriction coefficients at all surfaces in the given setup is μs=0.5 μk=0.20 .Find the minimum acceleration of the block of mass 2kg so that smaller block of mass 0.5kg remains at rest wrt 2kg (g=10ms2)
View SolutionFriction coefficients at all surfaces in the given setup is μs=0.5 μk=0.20 .Find the minimum acceleration of the block of mass 2kg so that smaller block of mass 0.5kg remains at rest wrt 2kg (g=10m/s^(2))
View SolutionFriction coefficients at all surfaces in the given setup is μs=0.5 μk=0.20 .Find the minimum acceleration of the block of mass 2kg so that smaller block of mass 0.5kg remains at rest wrt 2kg (g=10m/s^(2))
View SolutionIn the figure (g=10m/s2 ) .Acceleration of 2kg block is :
 View Solution
View SolutionIn the figure-2.205 shown in blocks A, B and C has masses mA=5kg,mB=5kg and mC=10kg respectively, find the acceleration of the three blocks. Assume all pulleys and strings are ideal. (Take g=10m/s2)
 View Solution
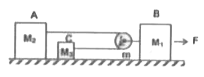
View SolutionThree blocks, placed on smooth horizontal surface are connected by ideal string and a disc shaped pulley of radius r, and mass m. Find the accelerations of the blocks. Masses of the blocks are given as M1=10kg,M2=5kg,M3=2kg,m=2kg.
 View Solution
View SolutionA 2 kg block A is attached to one end of a light string that passes over an an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of 5m/s2 with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the steing. [g=10m/s2]
 View Solution
View Solution

