The coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
To solve the problem, we will break it down into two parts as stated in the question.
Part a: Finding the Maximum Angle θ
1. Identify the Forces Acting on the Block:
- The weight of the block mg acts vertically downward.
- The normal force N acts perpendicular to the incline.
- The frictional force f acts parallel to the incline, opposing the motion.
2. Resolve the Weight into Components:
- The component of weight acting perpendicular to the incline: mgcosθ
- The component of weight acting parallel to the incline: mgsinθ
3. Apply the Condition for Static Equilibrium:
- For the block to not slip, the maximum static frictional force must equal the component of the weight acting down the incline:
fmax=μsN
- Here, N=mgcosθ, so:
fmax=μs(mgcosθ)
4. Set Up the Equation:
- At the point of impending motion:
μs(mgcosθ)=mgsinθ
5. Cancel out mg (assuming m≠0):
μscosθ=sinθ
6. Rearranging the Equation:
tanθ=μs
7. Substituting the Given Coefficient of Static Friction:
- Given μs=0.3:
θ=tan−1(0.3)
8. Calculate θ:
- Using a calculator:
θ≈16.7∘
Part b: Finding the Frictional Force when the Incline is at θ/2
1. Determine the New Angle:
- The angle of the incline is now θ/2.
2. Calculate the Forces at θ/2:
- The weight components are:
- Perpendicular: mgcos(θ/2)
- Parallel: mgsin(θ/2)
3. Static Friction Condition:
- Since the block does not slip, the frictional force f must balance the component of the weight acting down the incline:
f=mgsin(θ/2)
4. Substituting for θ:
- From part a, we know θ=tan−1(0.3). Therefore:
f=mgsin(tan−1(0.3)2)
5. Final Expression for Frictional Force:
- The frictional force can be calculated using the mass m and the known value of g (acceleration due to gravity).
Summary of the Solution:
- Maximum angle θ: θ≈16.7∘
- Frictional force at θ/2: f=mgsin(tan−1(0.3)2)
- The weight of the block mg acts vertically downward.
- The normal force N acts perpendicular to the incline.
- The frictional force f acts parallel to the incline, opposing the motion.
- The component of weight acting perpendicular to the incline: mgcosθ
- The component of weight acting parallel to the incline: mgsinθ
- For the block to not slip, the maximum static frictional force must equal the component of the weight acting down the incline:
fmax=μsN
- Here, N=mgcosθ, so:
fmax=μs(mgcosθ)
- At the point of impending motion:
μs(mgcosθ)=mgsinθ
μscosθ=sinθ
tanθ=μs
- Given μs=0.3:
θ=tan−1(0.3)
- Using a calculator:
θ≈16.7∘
- The angle of the incline is now θ/2.
- The weight components are:
- Perpendicular: mgcos(θ/2)
- Parallel: mgsin(θ/2)
- Since the block does not slip, the frictional force f must balance the component of the weight acting down the incline:
f=mgsin(θ/2)
- From part a, we know θ=tan−1(0.3). Therefore:
f=mgsin(tan−1(0.3)2)
- The frictional force can be calculated using the mass m and the known value of g (acceleration due to gravity).
- Maximum angle θ: θ≈16.7∘
- Frictional force at θ/2: f=mgsin(tan−1(0.3)2)
Topper's Solved these Questions
- FRICTIONBook:HC VERMA ENGLISHChapter:FRICTIONExercise:Objective -1
Explore 10 Videos
- FRICTIONBook:HC VERMA ENGLISHChapter:FRICTIONExercise:Objective -2
Explore 5 Videos
- FRICTIONBook:HC VERMA ENGLISHChapter:FRICTIONExercise:Questions for short Answer
Explore 11 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
- GRAVITATIONBook:HC VERMA ENGLISHChapter:GRAVITATIONExercise:Question for short Answers
Explore 18 Videos
Similar Questions
A block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mgA block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionThe coefficient of friction between the block A of mass m and the triangular wedge B of mass M is μ. There in no friction between the wedge and the plane if the system (block A+ wedge B) is released so that there is no stiding between A and B find the inclination θ

View Solution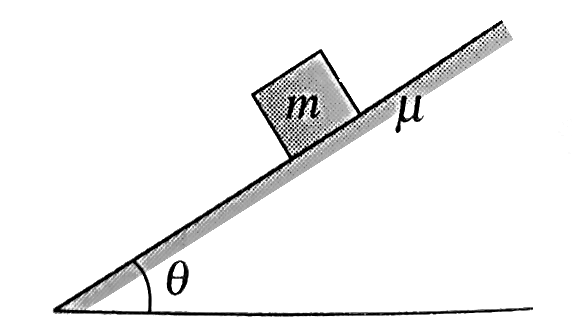 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:
View Solution A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:
View Solution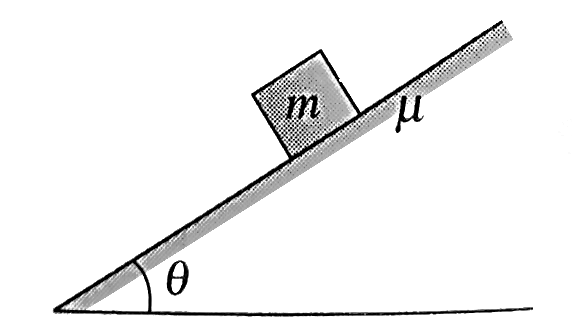 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If the entire system, were accelerated upward with acceleration a the angle of repose, would:
View Solution