For what value of x, the point P on the rod of length l=6m has zero acceleration if a force F is applied at the end of rod as shown.

a=Fm
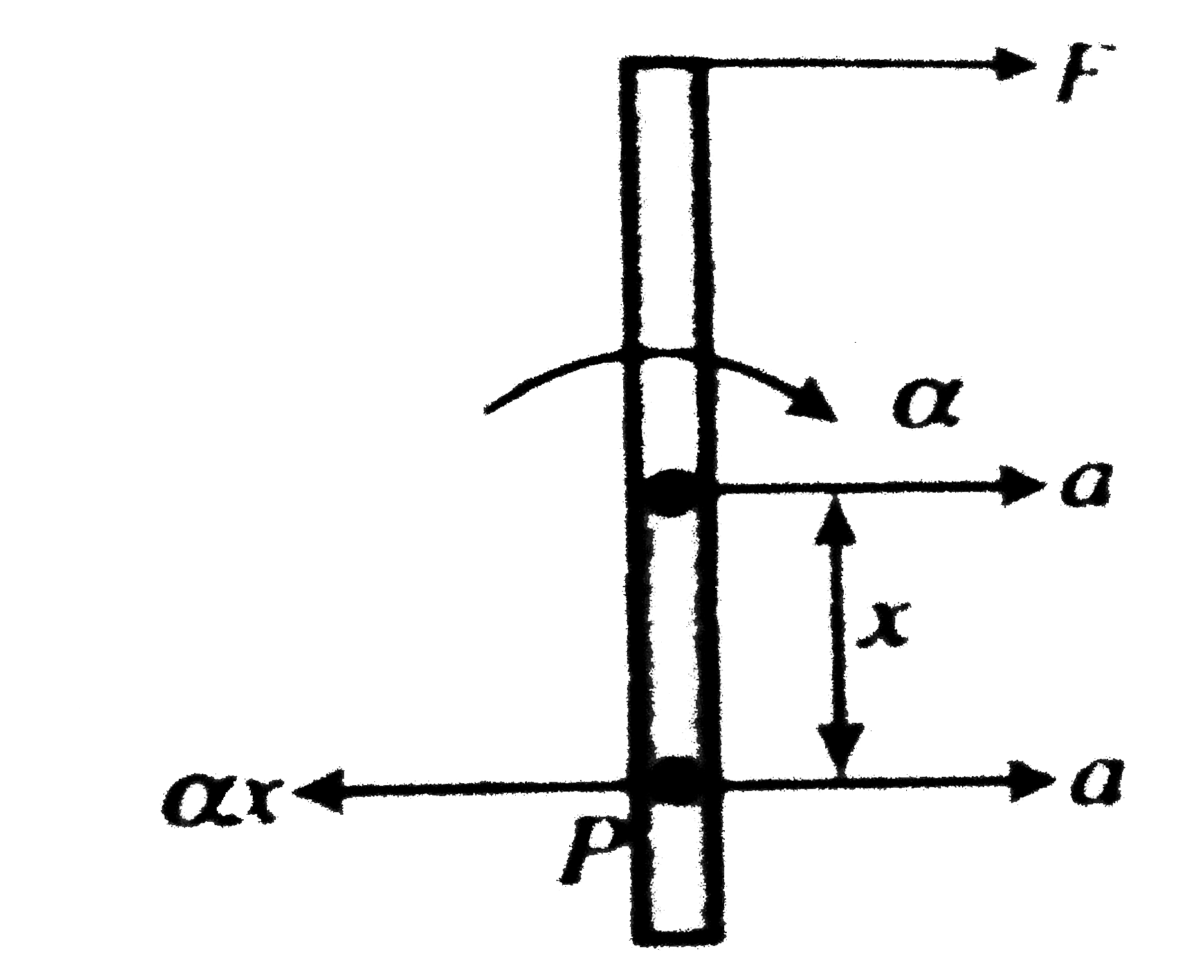
α=τI=Fl2ml2/12=6Fml
aP=a−ax=0
⇒fm−6Fml=x=0⇒x=l6=1m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct97videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.315videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
 View Solution
View SolutionA uniform rod of mass M and length L is hinged at its lower end on a table. The rod can rotate freely in vertical plane and there is no friction at the hinge. A ball of mass M and radius R=L3 is placed in contact with the vertical rod and a horizontal force F is applied at the upper end of the rod.
(a) Find the acceleration of the ball immediately after the force starts acting.
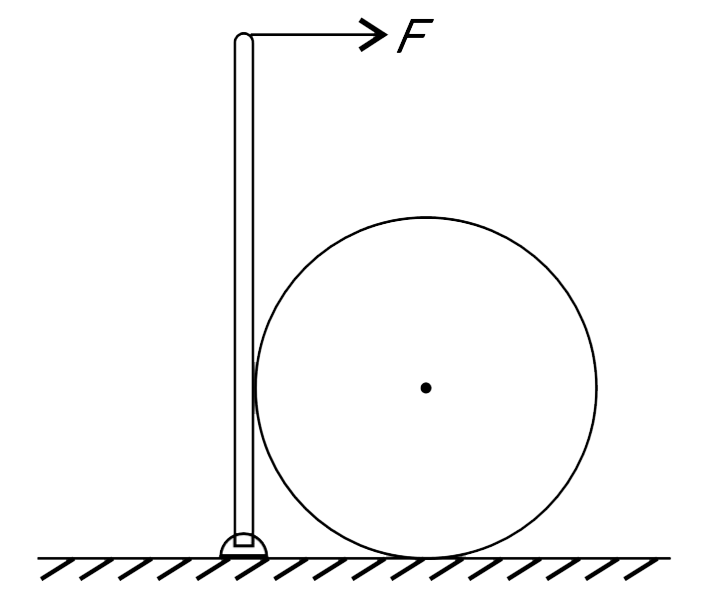
(b) Find the horizontal component of hinge force acting on the rod immediately after force F starts acting.View Solution
Knowledge Check
- Question 1 - Select One
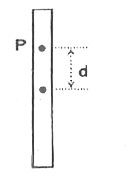
A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
The time period of this pendulum when d = L/2 will beA2π√2l3gB2π√3l2gC4π√l3gD2π3√2lg - Question 2 - Select One
A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
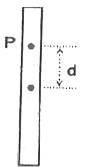
Time period will be minimum when d is equal toAL√12BL√6CL/4DL/2 - Question 3 - Select One
A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
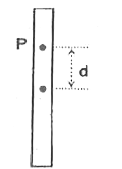
As d changes from L/2 to zero. Time periodAincreases continuouslyBdecreases continuouslyCfirst increases then decreaseDfirst decreases then increase
A pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

As d changes from L/2 to zeroView SolutionA pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

The time period of this pendulum when d = L/2 will beView SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
 View Solution
View SolutionA long thin rod of length 2L rotates with a constant angular acceleration of 10rad/s2 about an axis that is perpendicular to the rod and passes through its center.
What is the ratio of the tangential acceleration of a point on the end of the rod to that of a point a distance L/2 from the end of the rod?View SolutionA long thin rod of length 2L rotates with a constant angular acceleration of 10rad/s2 about an axis that is perpendicular to the rod and passes through its center.
What is the ratio of the centripetal acceleration of a point on the end of the rod to that of a point a distance L/2 from the end of the rod?View Solution

