Find aC and α of the smooth rod of mass m and length l.
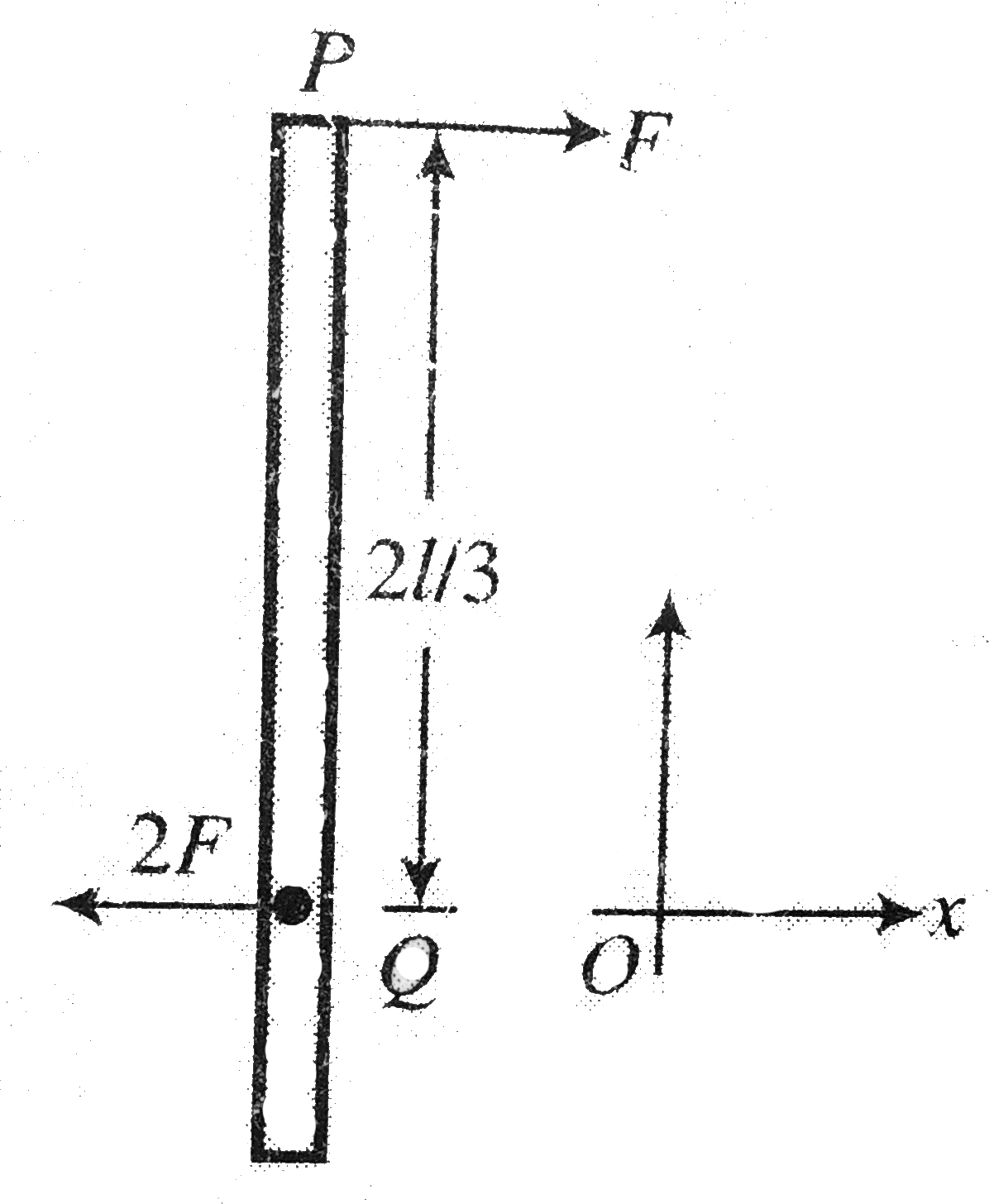
Force equation
F−2F=ma⇒a=−Fm
Hence →a=−Fmˆi
Torque equation about centre of mass
F.l2+(23−l2)=lCα
F.l2+Fl6=ml212.α
32Fl=ml212.α⇒8Fml
Hence →α=(8F).(ml)ˆk
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct97videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.315videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
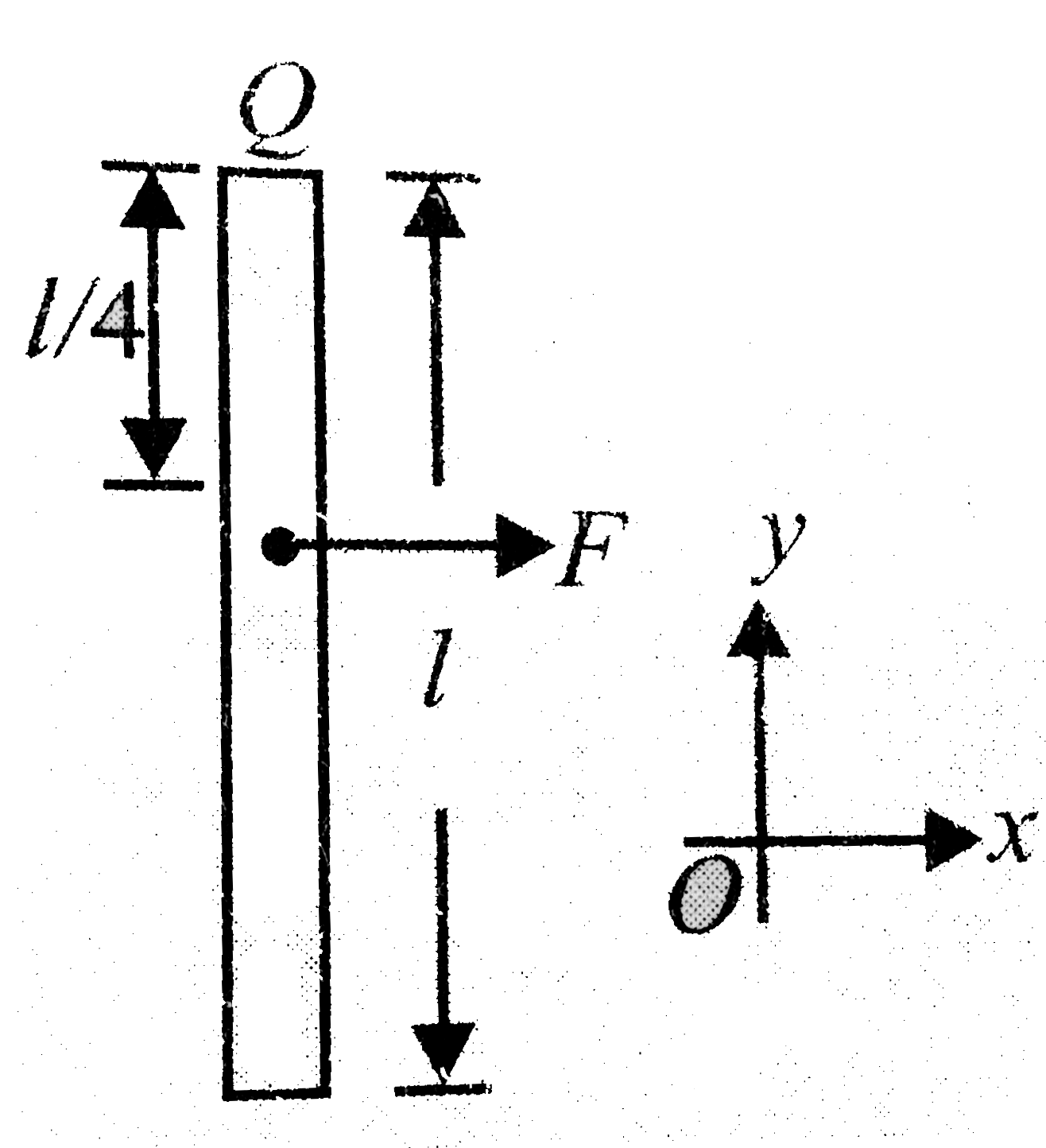 Find α,aQ and the point of zero acceleration when the horizontal force F acts on the smooth rod of mass m and length l which is kept on a horizontal surface. View Solution
Find α,aQ and the point of zero acceleration when the horizontal force F acts on the smooth rod of mass m and length l which is kept on a horizontal surface. View SolutionA ball of mass m collides elastically with a smooth hanging rod of mass M and length l.
a. If M=3m find the value of b for which no horizontal reaction occurs at the pivot.
b. For what value of m/M the ball falls dead just after the collision assuming e=(12)?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Find the potential energy of the gravitational interaction of a point mass m and a rod of mass m and length l, if they are along a straight line. Point mass is at a distance of a from the end of the rod.

Find the potential energy of the gravitationalAU=−Gm2lln(2a+l2a−l)BU=−Gm2l2ln(2a+l2a−l)CU=−Gm2l2ln(2a−l2a+l)DU=−Gm2l2ln(2a−l2a+l)2 - Question 2 - Select One
Moment of inertia of a thin rod of mass 'M' and length 'L' perpendicular to rod at mid point is
AMl22,BMl23CMl212DNone of these - Question 3 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)L
find the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its eneds and perpendicular to its length.
View SolutionFind the M.I. of thin uniform rod of mass M and length L about the axis as shown.
 View Solution
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.
 View Solution
View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
View SolutionCalculate the moment of inertia of a thin rod of mass m and length l about a symmetry axis through the centre of mass and perpendicular to the length of the rod, as shown in Fig.
 View Solution
View Solution

