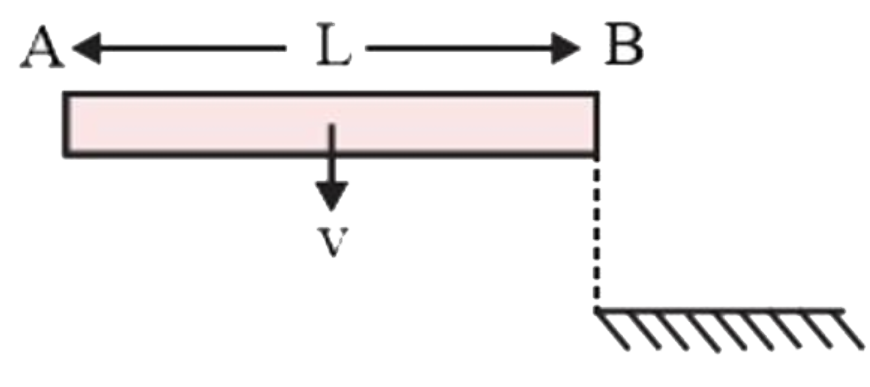
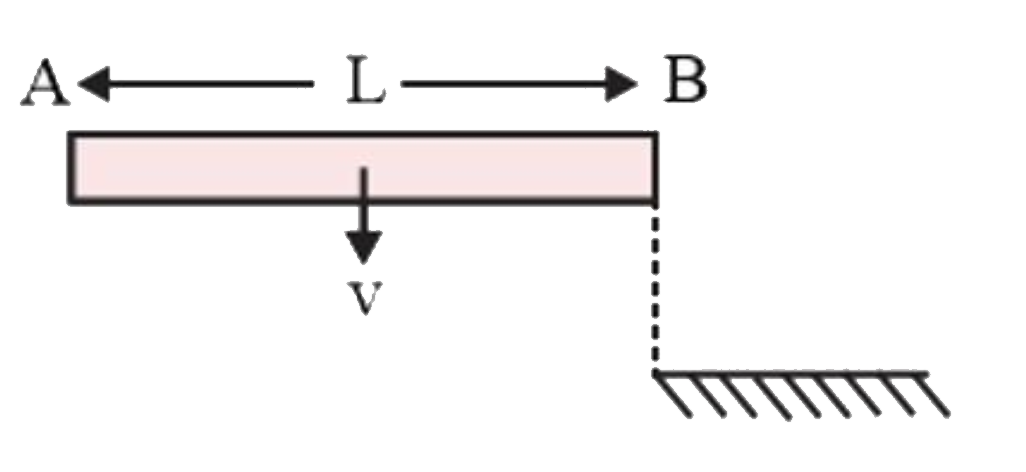
In the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be

v2L
vL
v√32L
none of these
The correct Answer is:B

The velocities of the ends A and B along the length of rod should be the same.
Hence vAcos30∘=vBcos30∘⇒vA=vB=v
Hence the angular velocity of the rod is
ω=(vAB)⊥l=2vsin30∘limpliesω=vl
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.
 View Solution
View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the figure shown the instantaneous speed of end A of the rod is v to the left the angular velocity of the rod of lengthL must be
 Av/2LBv/LCv√3/2LDnone
Av/2LBv/LCv√3/2LDnone - Question 2 - Select One
In the figure shown a smooth ring is connected to rod AB, while rod CD passes through ring. At the given instant angular velocity of rod AB about hinge A is 1 rod/s and AC=CB. Instantaneous angular velocity of rod CD about hinge C is
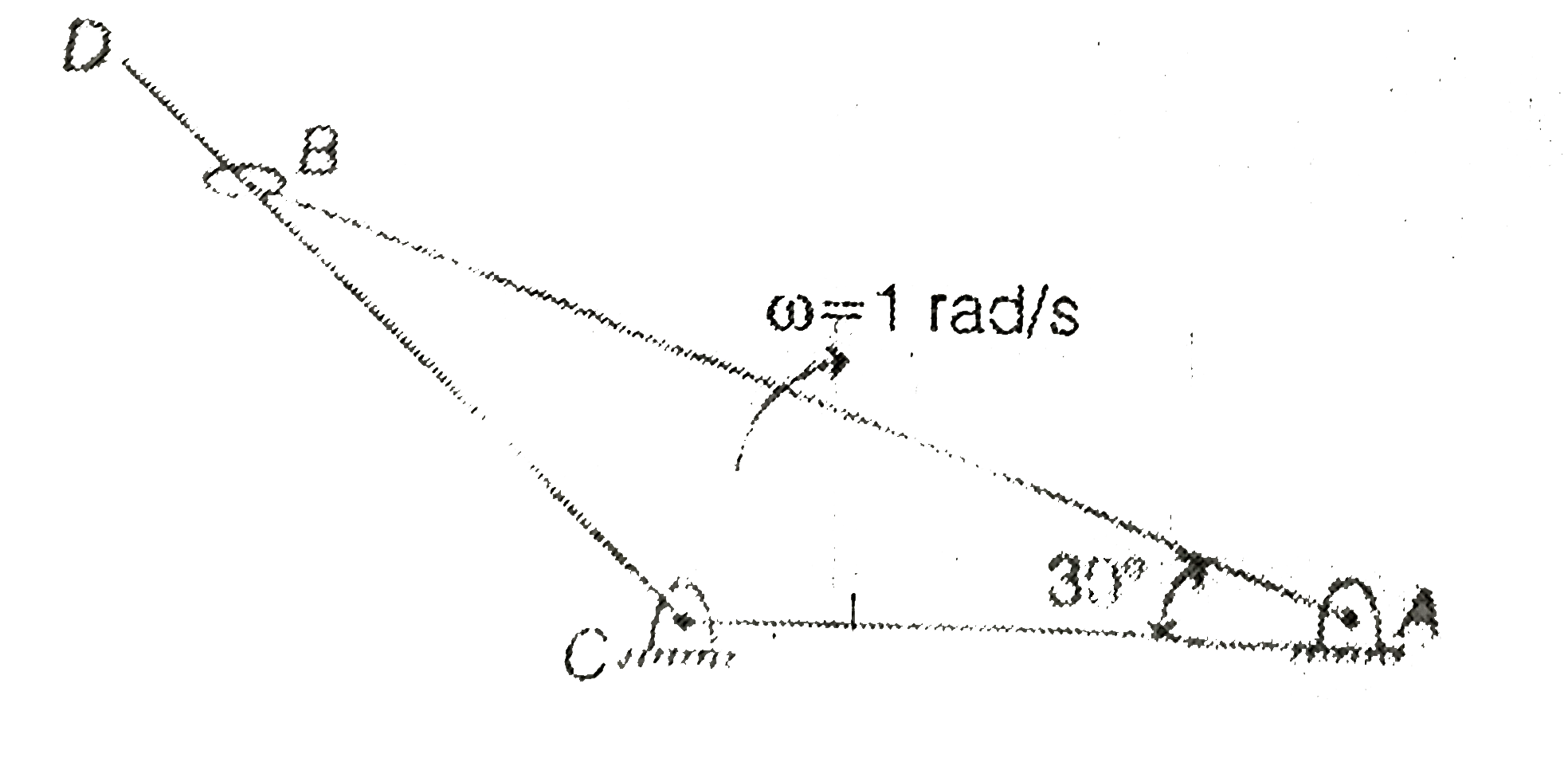 A1rad/sB1/2rad/sC√3/2rad/sD3/2rad/s
A1rad/sB1/2rad/sC√3/2rad/sD3/2rad/s - Question 3 - Select One
Consider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
Av/LB2v/LC3v/2LD6v/L
A rod AB of length L and mass M is free to move on a frictionless horizontal surface . It is moving with a velocity v , as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact , the angular velocity of the rod AB , just after
 View Solution
View SolutionA rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of A mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
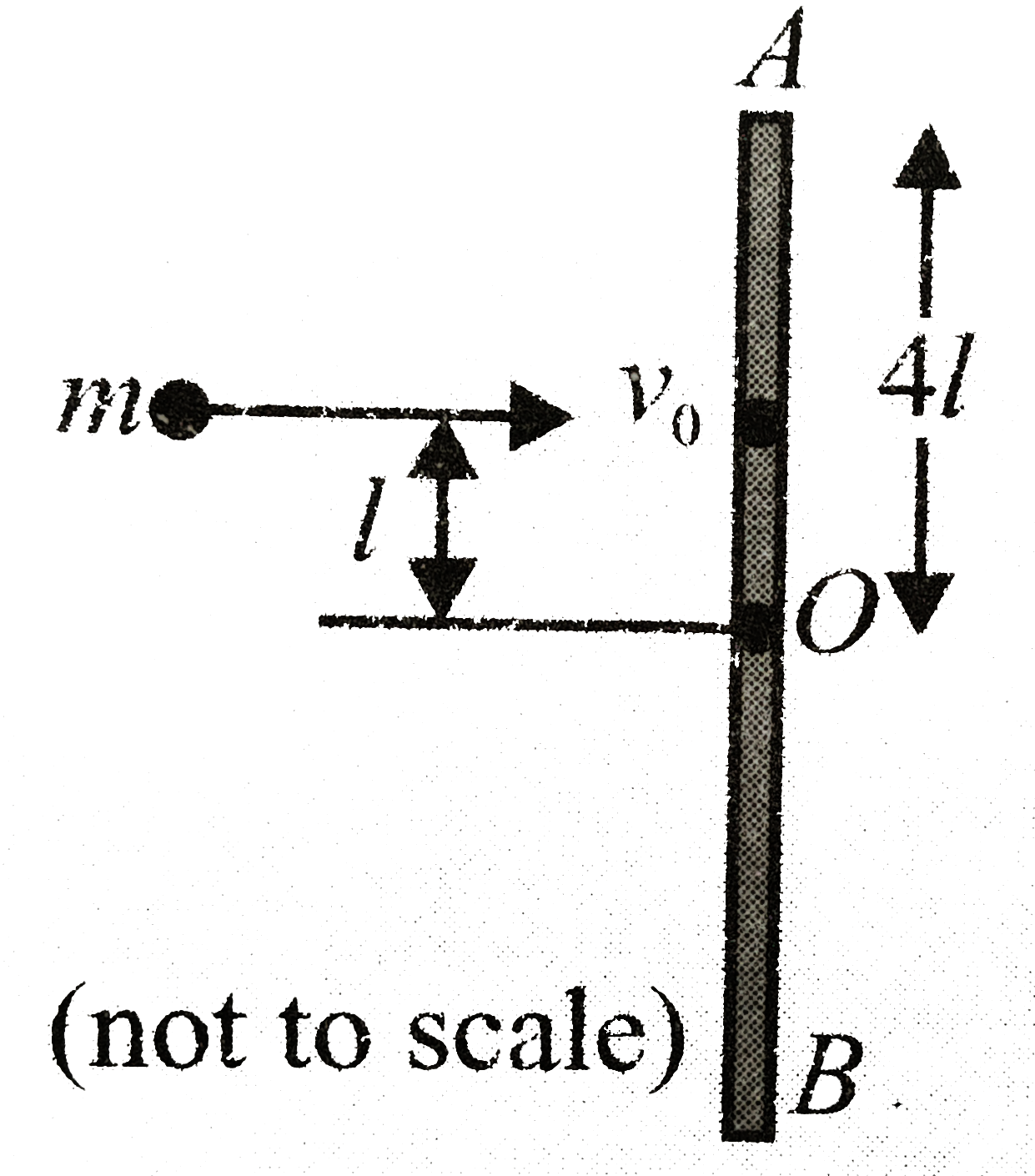 View Solution
View Solution
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.View SolutionA uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L/4 from the right end. The tension in the second rope is.
 .View Solution
.View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
 View Solution
View Solution

