Two beads each of mass m are welded at the ends of two light rigid rods each of length l. if the pivots are smooth, find the ratio of translational and rotational kinetic energy of system.
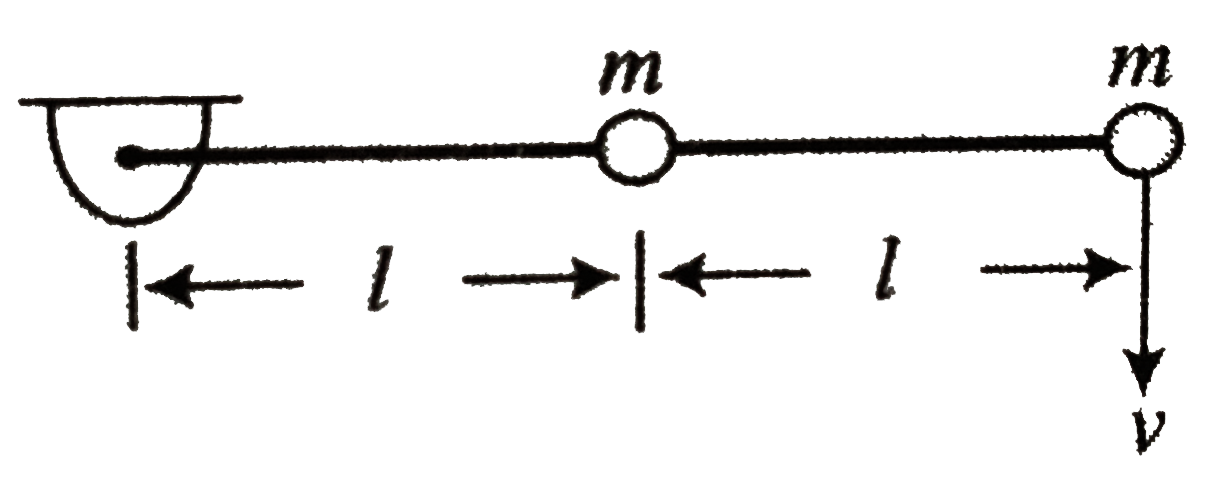
We know transltional kinetic energy Kr=12ICω2
Distance of centre of mass from pivot end
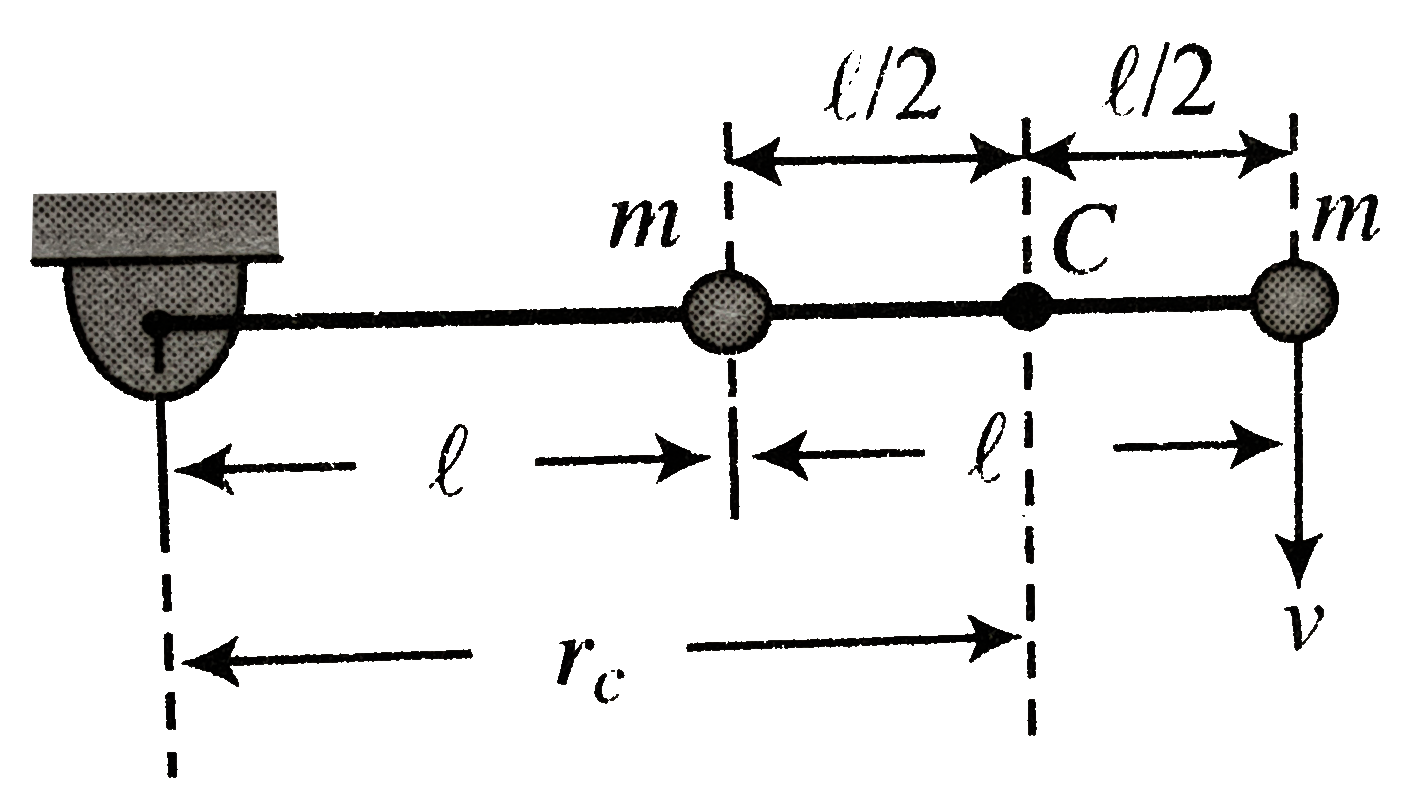
rC=ml+m(2l)m+m=32l
Moment of inertia of system about centre of mass
and IC=m(l2)2+m(l2)2=ml22
Angular velocity of rod ω=v2l
velocity of centre of mass
vcm=ω(32l)=(v2l)(32l)=34v
Translation kinetic energy of system
Ktranslation12Mtotal.v2cm=12(2m)(34v)(2)=916mv2
Krotational=12ICMω2=12((ml)2)2(v2l)2=116mv2
this gives KrKr=9
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
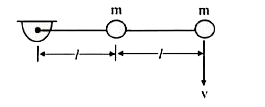
Two beads each of mas m are fixed at the ends of two light rigid rods each of length l as shown in the figure. If the pivot is smooth. Calculate the ratio of translational and rotational kinetic energy of system.
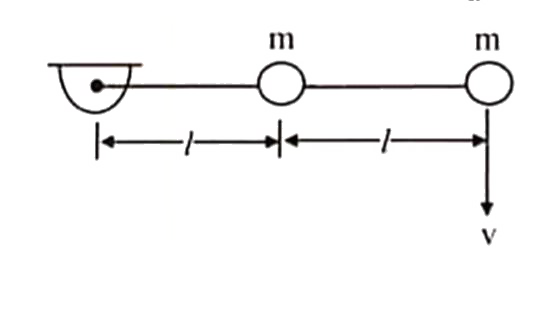
View SolutionTwo beads each of mass m are fixed on a light rigid rod of length 2l which is free to rotate in a horizontal plane. The bead on the far end is given some velocity υ as shown in the figure. If Kcm represents the kinetic energy of the centre of mass of the system and KR represents the rotational kinetic energy of the system, then what is the value of KcmKR?
View Solution
Knowledge Check
A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
A23π2f2ml2B43f2ml2C4π2f2ml2DzeroA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
A23π2f2ml2B43f2ml2C4π2f2ml2DZeroTwo particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
AqmB2qmCq2mDqπm
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionTwo small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View Solution
