A uniform disc of radius R rolls perfectly over two horizontal plank A and B moving with velocities v and 2v, respectively. Find the
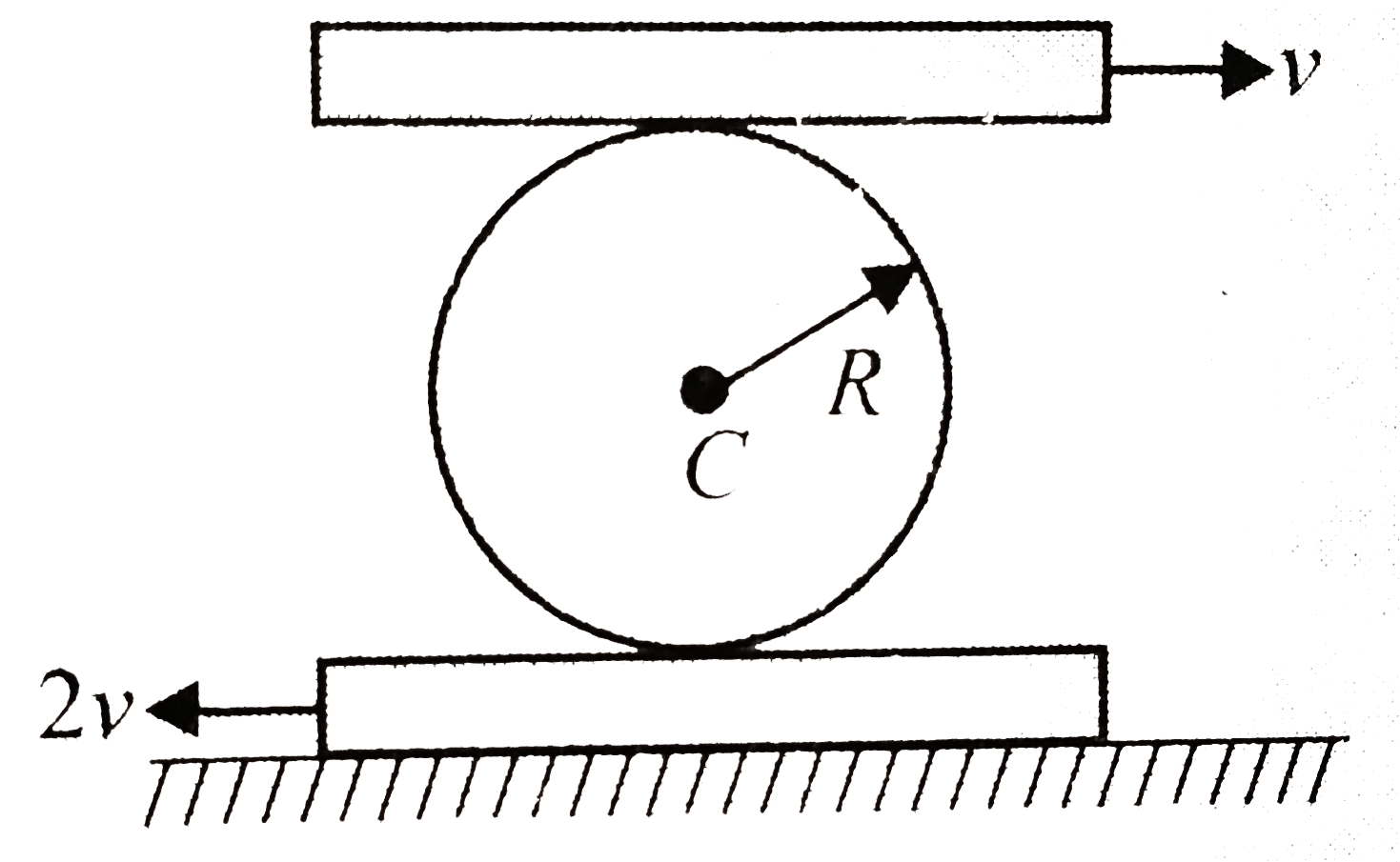
a. velocity of CM of the disc.
b. angular velocity of the disc.
As the disc is rolling points A and B in which are on the disc and in contact with the planks will no slide. The velocities of points A and B should be the same as the planks. Let the disc rotate with an angular velocity ω and let the velocity of centre of the mass of the disc be vc.
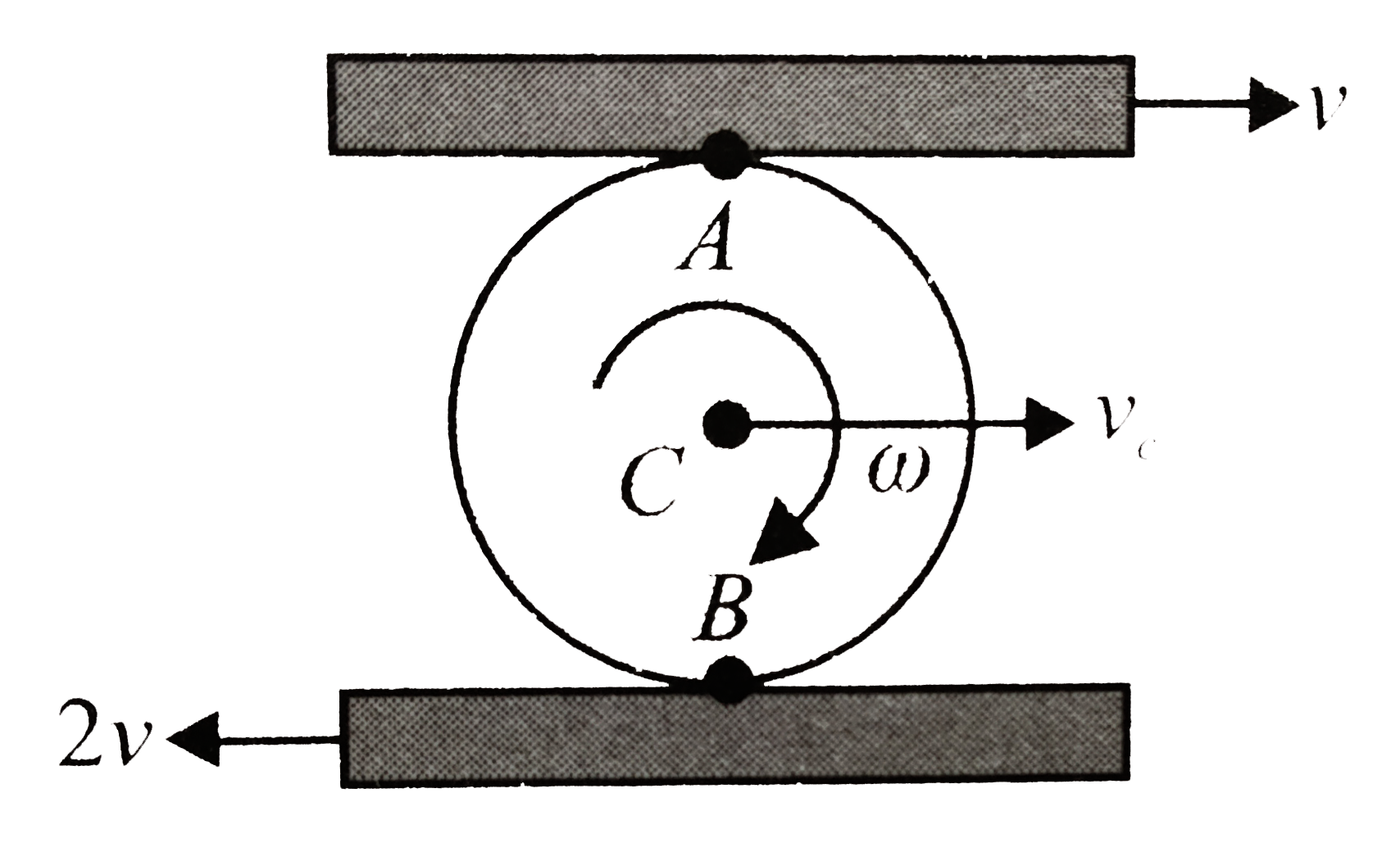
Velocity of point A,vA,vc+ωR=v...........i
Velocity of point B,vB,ωR−vc=2v..........ii
From eqn i and ii ω=3v/R and vc=−2v
Hence velocity of centre of disc will be 2v towards the left and the angular velocity will be 3v/R the in the clockwise sense.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A uniform disc of radius R rolls perfectly over two horizontal plank A and B moving with velocities v and 2v, respectively. Find the

a. velocity of CM of the disc.
b. angular velocity of the disc.
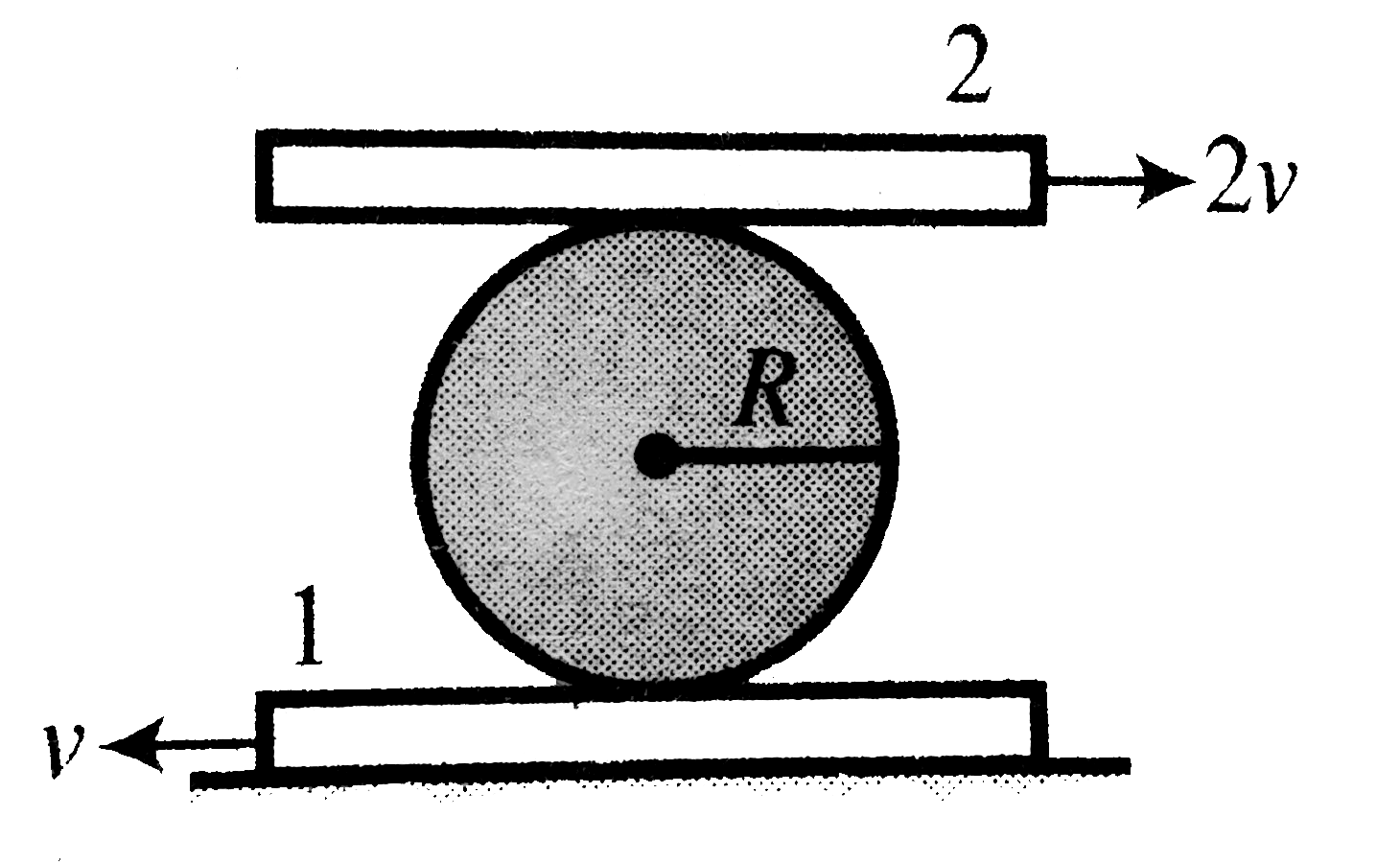
View SolutionA cylinder is rolling without sliding over two horizontal planks (surfaces) 1 and 2. If the velocities of the surfaces A and B are −vˆi and 2vˆi respectively, find the:
a. Position of instantaneous axis of rotation.
b. Angular velocity of the cylinder.
View Solution
Knowledge Check
A disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is
 A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwise
A3V2R AnticlockwiseB3V2R ClockwiseCV2R AnticlockwiseDV2R clockwiseA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
AIωI+mR2BIω+mvRI+mR2CIω−mvRI+mR2DIω−mvRIA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
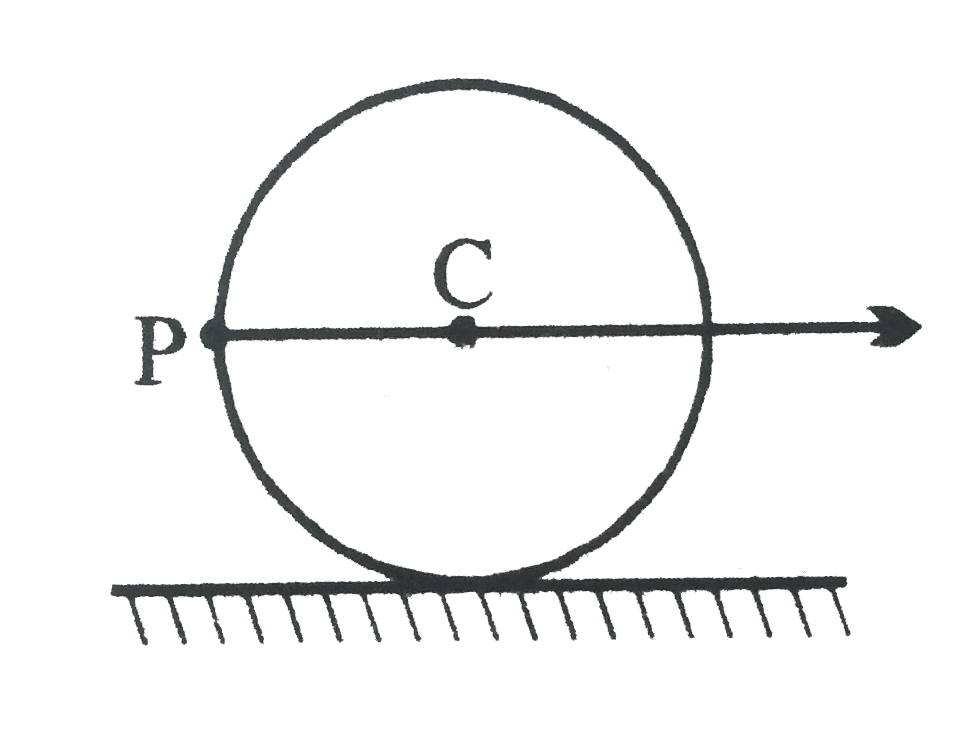 .AzeroB45∘C135∘Dtan−1(1/2)
.AzeroB45∘C135∘Dtan−1(1/2)
A small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
View Solution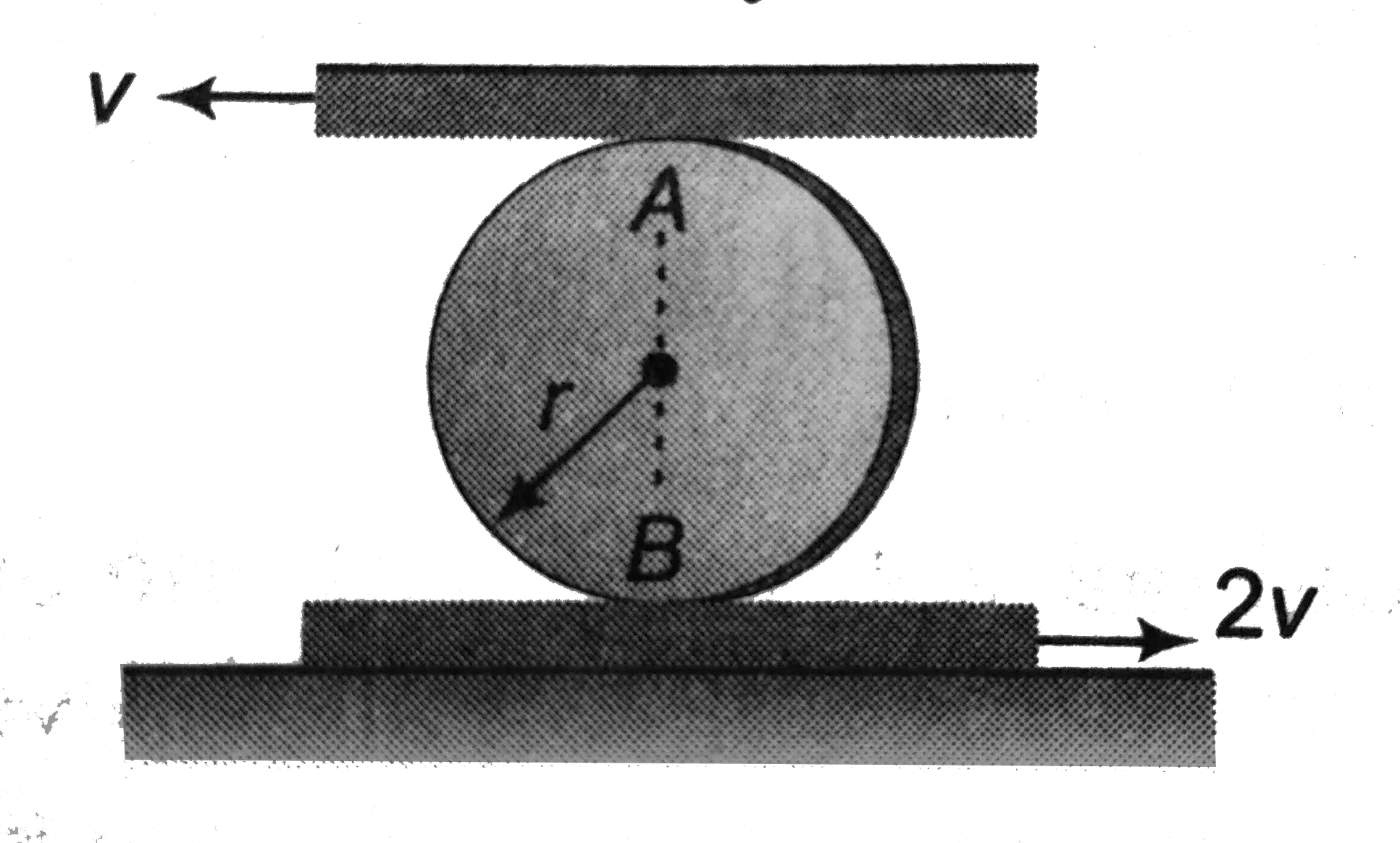
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : at the upper most point
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View Solution
