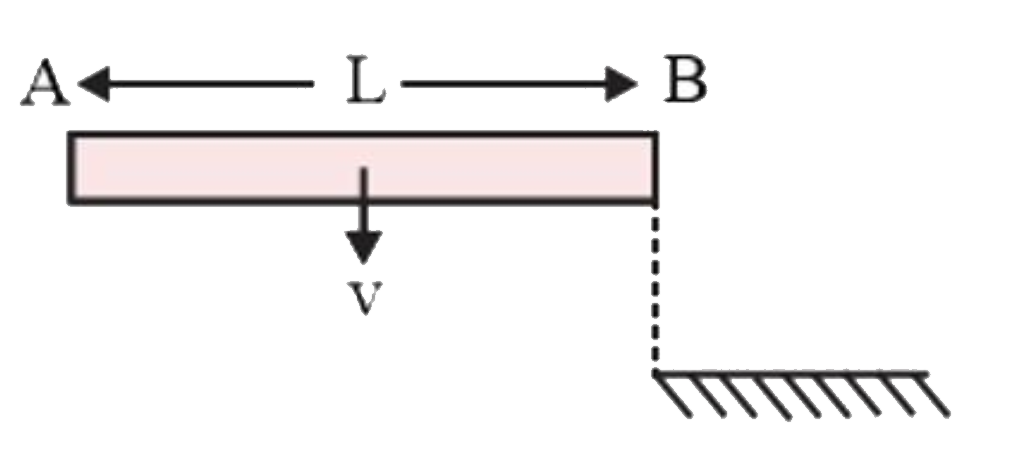
A uniform rod of lengh l moving with a downward velocity v0 strikes a peg P. If the coefficient of restitutioin of impact is e, find the velocity of CM of the rod just after impact.

Method 1: At the time of impact the force acting on the rod is N (upward) and mg (downward). Since normal reaction is an ampulsive force during impact, N>>mg. Then we disregard the effect of gravity during the impact.
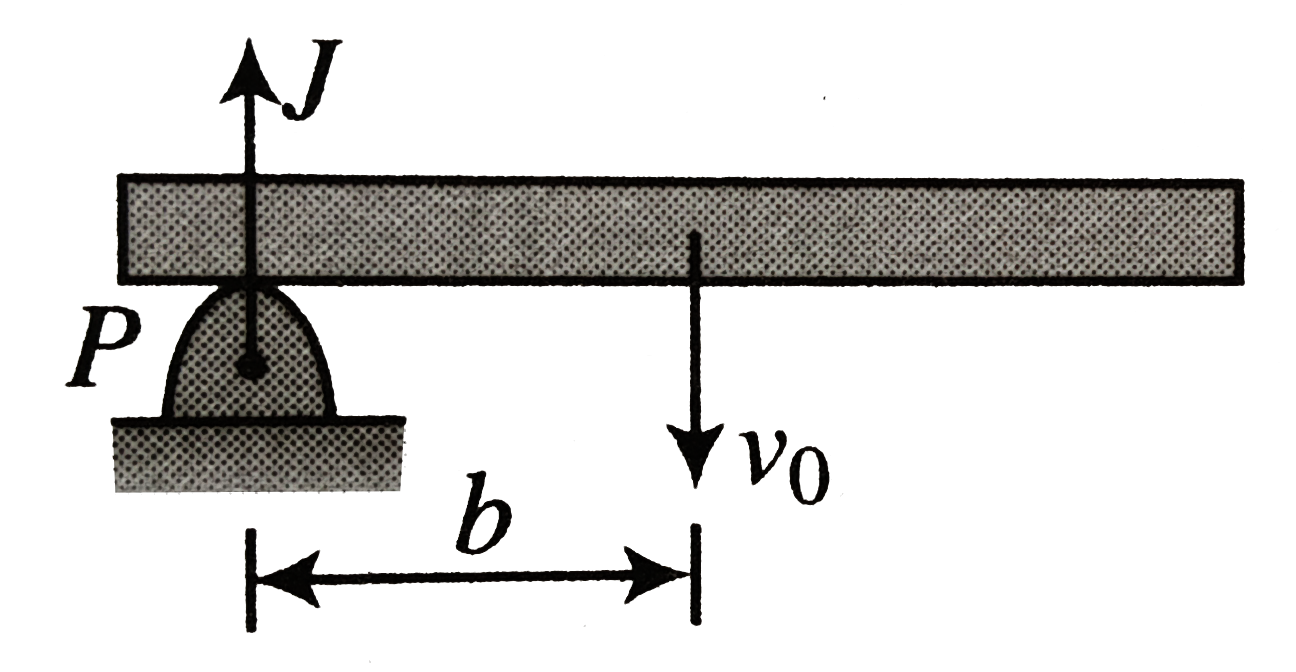
Impulse equation mv0=J=mv ..........i
The angular impulse of N is J.b=ml212ω
J=ml212bω...........ii
Adding eqn i and ii we have
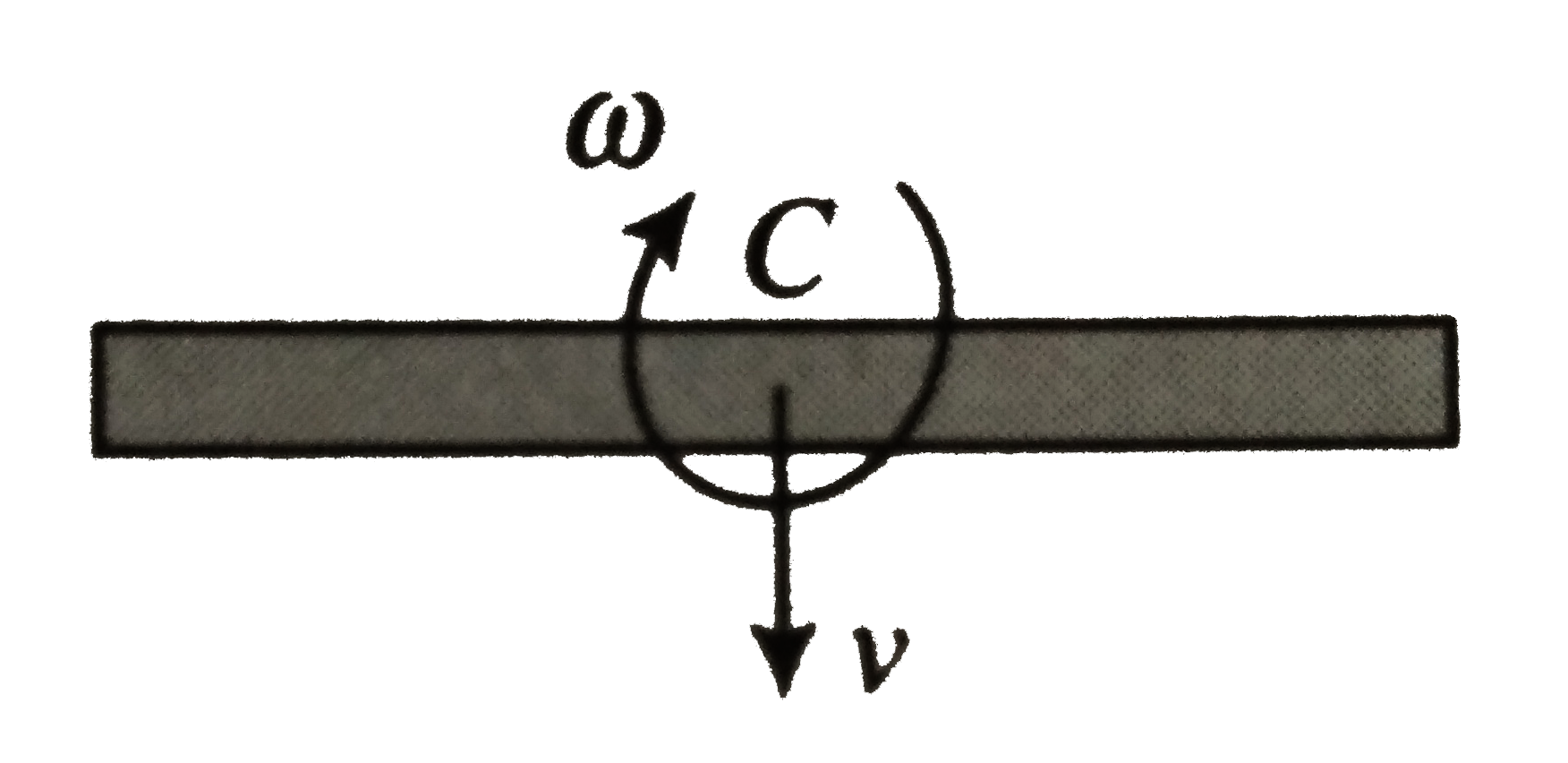
v0−v=l2ω12b.............iii
Newton's empirical formula gives us
vp=−v0 ..........iv
The velocity of P is →vP=→vPC+→vC
v−bω=−ev0..............v
Now we have two equan ii and iv for two unknowns v and ω,.
Solving these two equations we have v=12b2−el212b2+l2v0
Method 2: If we choose the fixed point at P, the angular impulse about P is zero because the impusle J passes through P during impact.
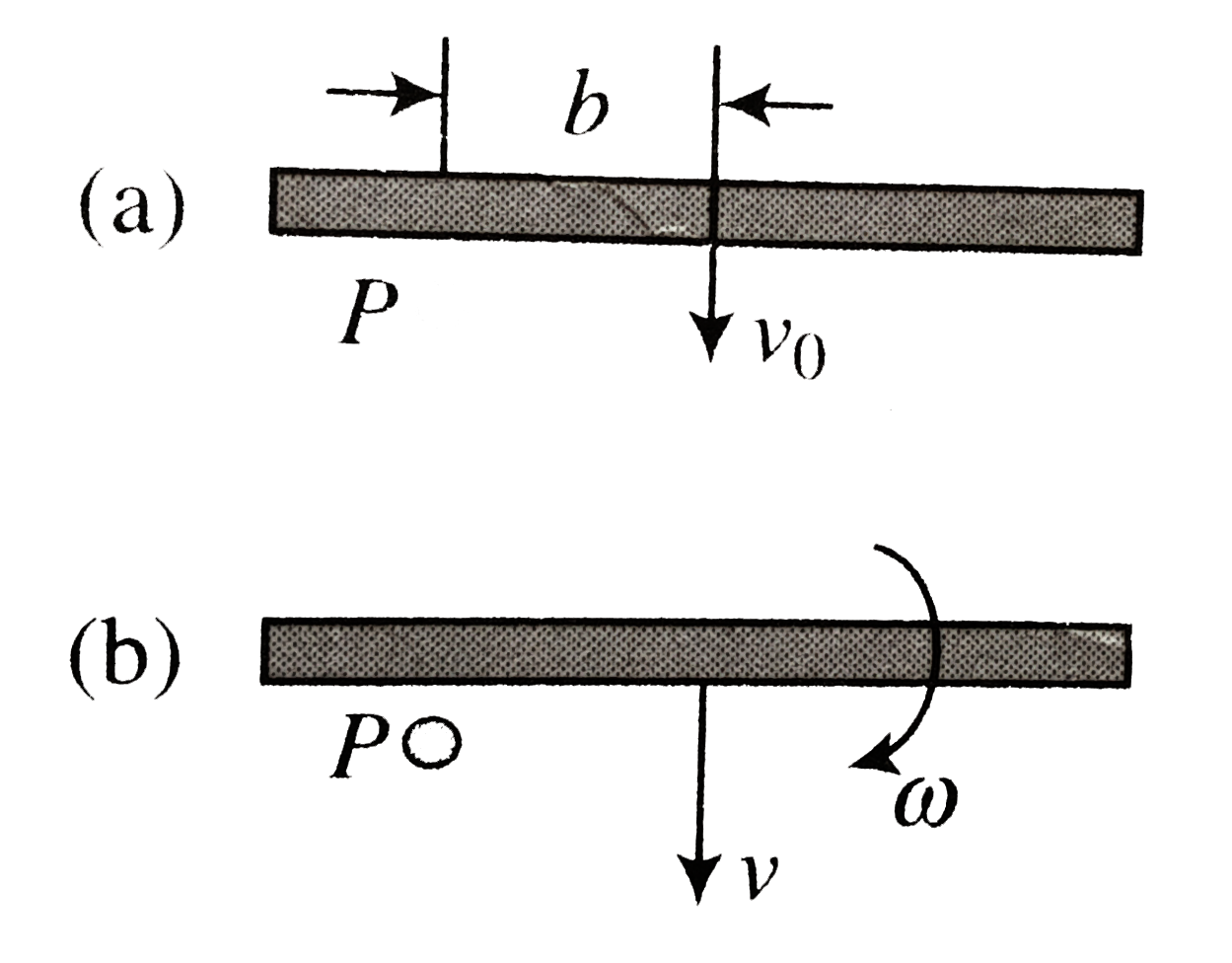
hence the angular momentum of the rod just before and just after the impact about remain constant.
→L1=→L2, where →L1=mv0b(−ˆk)
and →L2=ml212ω(−ˆk)+mvb(−ˆk)
Then mv0b=mvb+ml212ω
This gives v0−v=l2ω12b
The other equations remain as unchanged. Solving the above eqn we will obtain the same value of v.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A particle of mass m=1kg collides with the end with velocity v0=6ms−1 of a spinning rod of mass2m and length l=1m at the end of he rod. If the coefficient of restitution of collision e=(2/3), find the
a. velocity of the particle
b. angular velocity of the rod just after the impact.
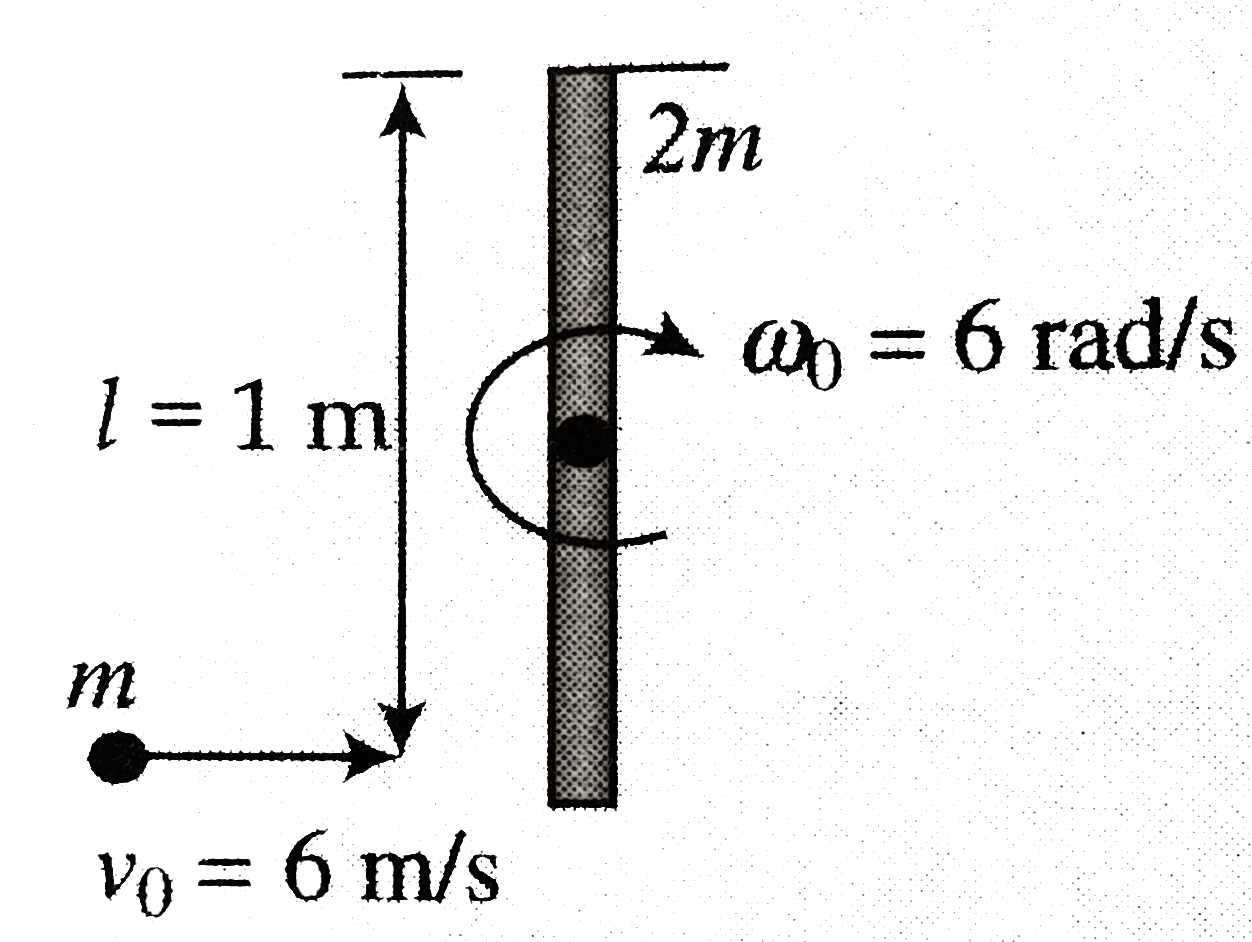
View SolutionA ball of mass m moving with velocity u impinges on a ball of mass em moving with velocity eu in the opposite direction. If the impact be direct and e be the coefficient of restitution then the velocity of the second ball after impact is the same as that of the first ball before impact.
View Solution
Knowledge Check
A sphere impinges directly on an equal sphere at rest. If the coefficient of restitution is e, their velocities after the impact are as
A1:eBe:1C1+e:1−eD1−e:1+eA homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0, then:
Aη>3Bη<3Cη>2Dη<6A homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0 then:
Aη>3Bη<3Cη>6Dη<6
A uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.
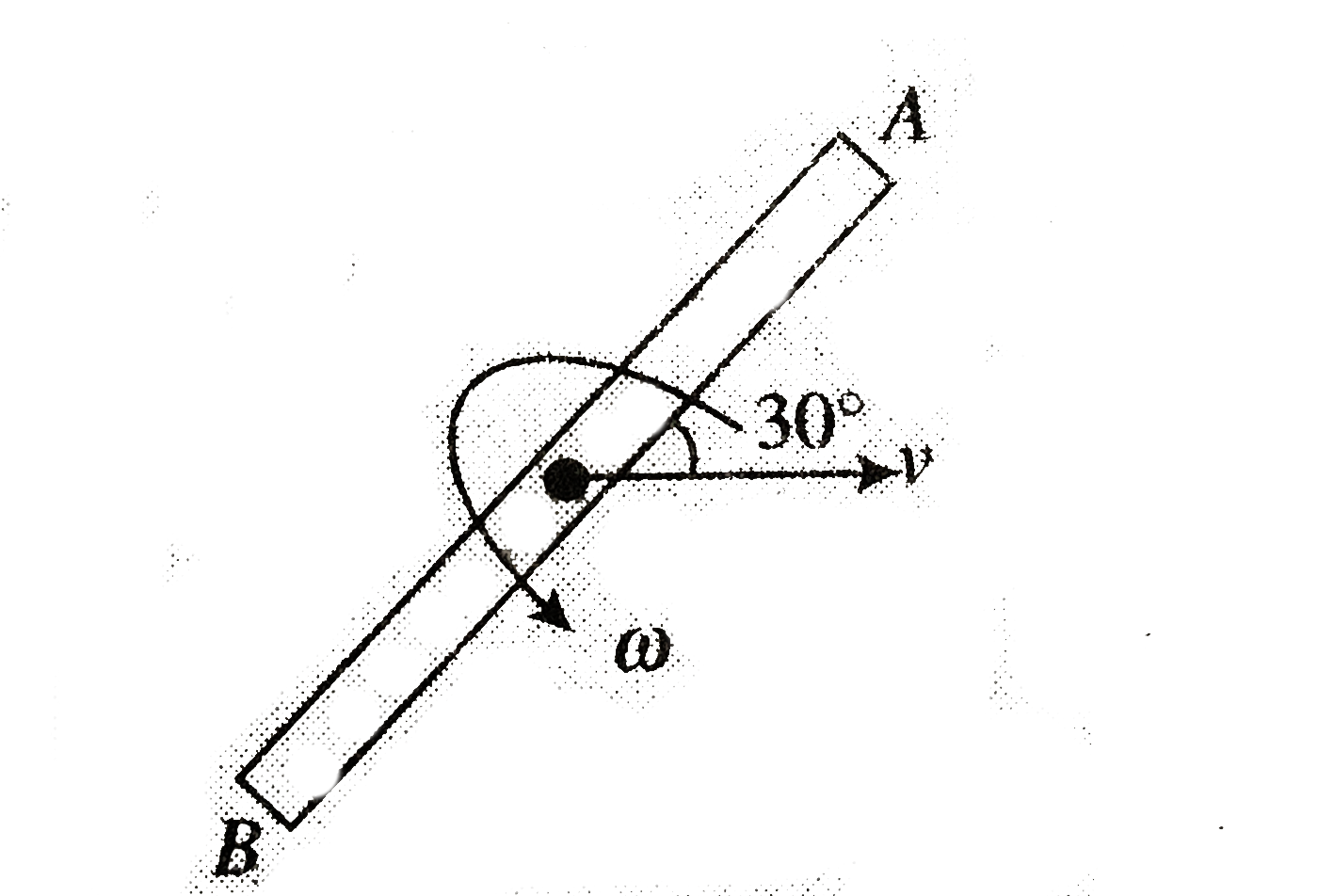
View SolutionA ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e.
(a) Find expression for the velocity of the ball immediately after the impact.
(b) If impact is perfectly elastic what do you observe?
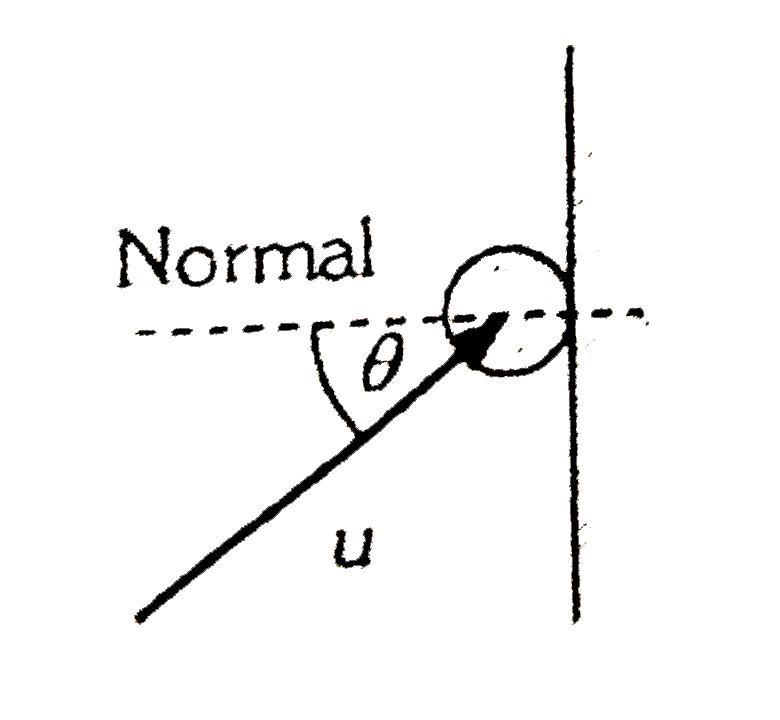
View SolutionA uniform rod of mass m and length l is released from rest from its vertical position by giving a gently push. In consequence, the end of the rod collides at P after rotating about the smooth horizontal axis O. If the coefficient of restitution e=(12). Find the: a. angular speed of the rod just after the impact.
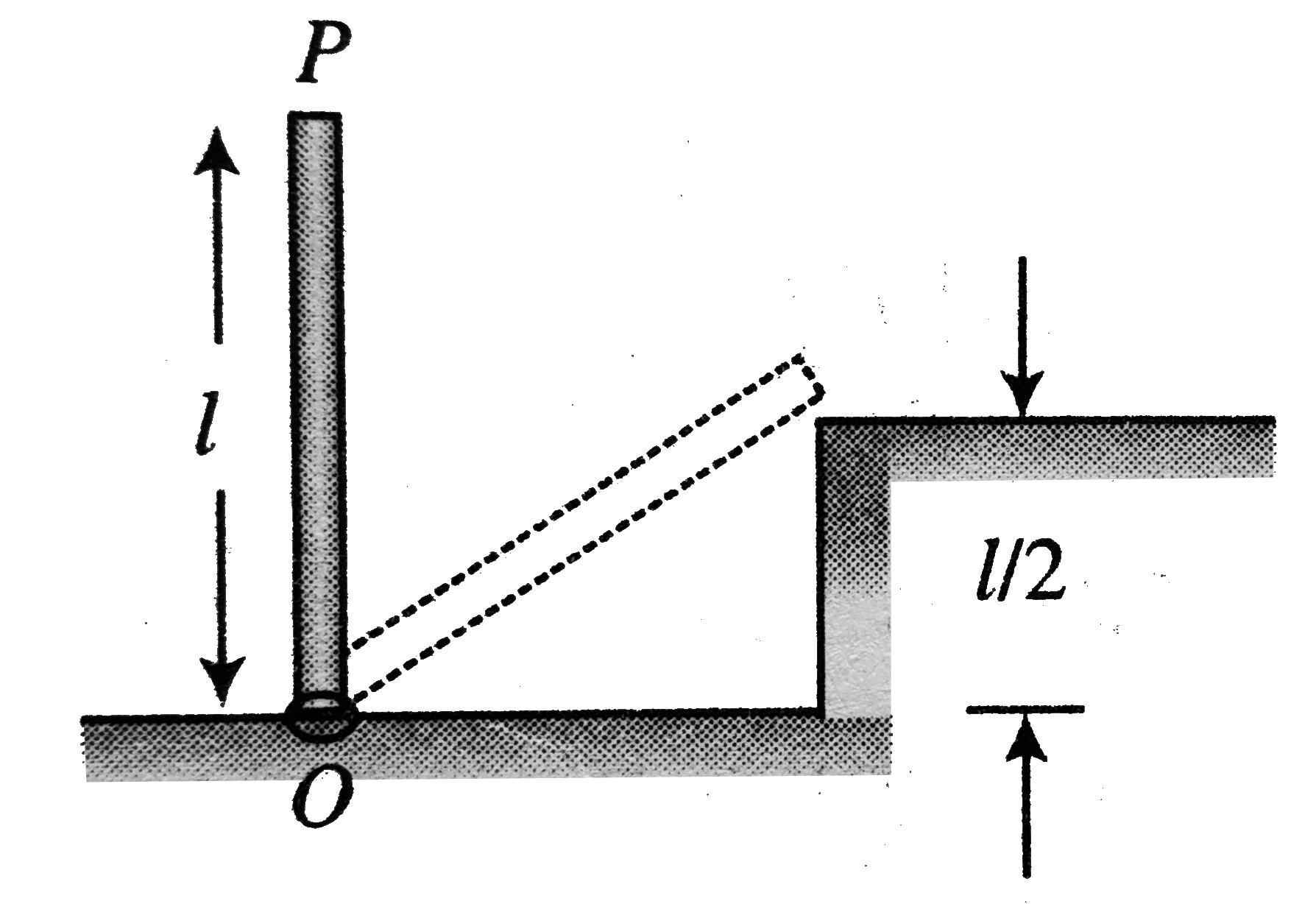
b. energy loss during collision. c. maximum angle rotated collision.
View SolutionA ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
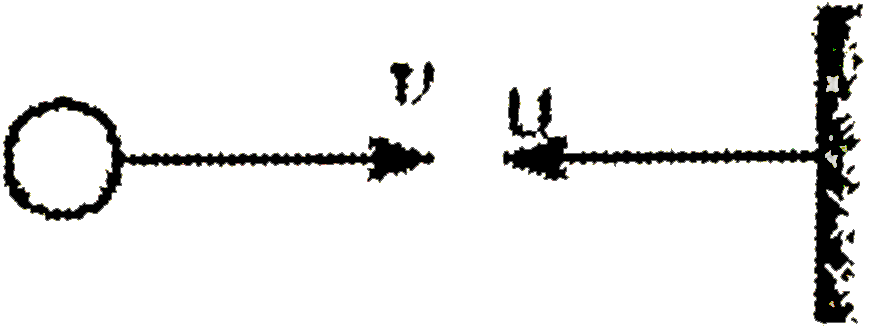
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
View Solution
