A ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e.
(a) Find expression for the velocity of the ball immediately after the impact.
(b) If impact is perfectly elastic what do you observe?
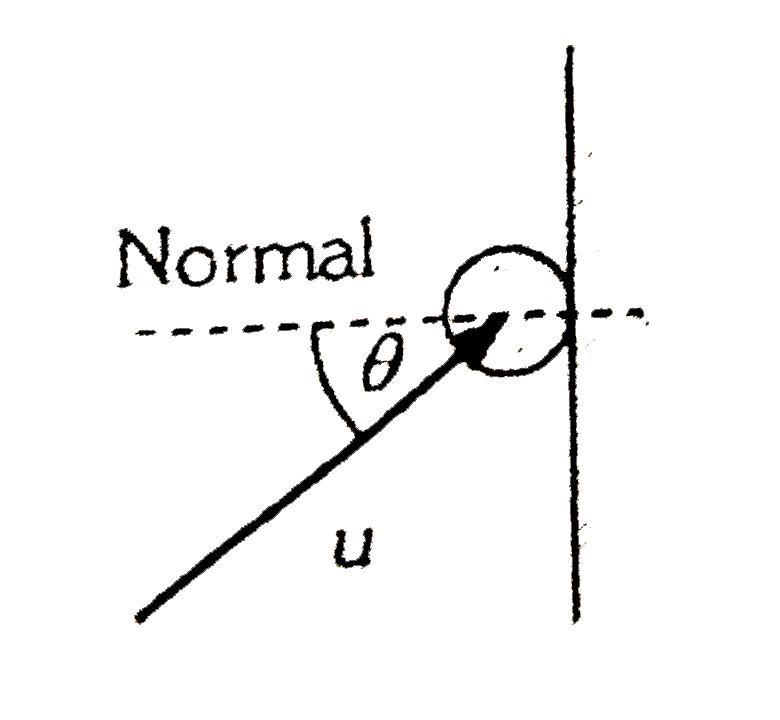
(a) Let us consider the ball as the body A and the wall as the body B. Since the wall has infinte,y large inertia (mass) as compared to the ball, the state of motion of the wall, emains unaltered during the impact i.e. the wall remain stationary.
Now we show velocities of the ball and its t and n-components immediately before and after the impact. For the purpose we have assumed velocity of the ball after the impact v.
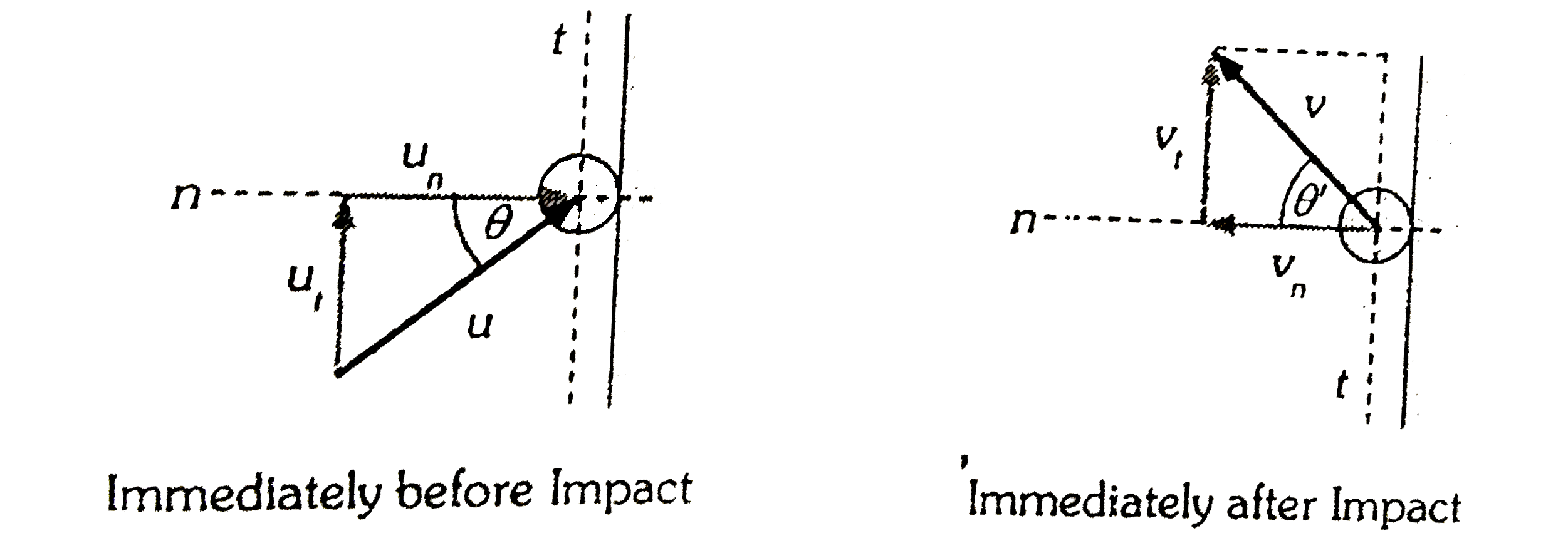
Component along t-axis Components of momentum along t-axis of the ball is conserved. Hence, t-component of velocities of each of the bodies remains unchanged. vt=ut=usinθ ...(i)
Component along -axis Concept of coefficient of restitution e is applicable only for the n-component velocities.
vBn−vAn=e(uAn−uBn)→−vn=eUn ,
From equations (i) and (ii), the t and n-components of velocity of the ball after the impact are
vt=usinθ and vn=eusinθ
(b) If the impact is perfectly elastic, we have vt=usinθ,vn=usinθ and θ=θ The ball will rebound with the same speed making the same angle with the vertical at which it has collided. In other words, a perfectly elastic collsion of a ball with a wall follows the same laws as light follows in reflection at a plane mirror.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two indentical balls A and B moving with velocities uA and uB In the same direction collide. Coefficient of restitution is e.
(a) Deduce expression for velocities of the balls after the collision.
(b) If collision is perfectly elastic, what do you observe?
View SolutionTwo indentical balls A and B moving with velocities uA and uB I the same direction collide. Coefficient of restitution is e.
(a) Deduce expression for velocities of the balls after the collision.
(b) If collision is perfectly elastic, what do you observe?
View Solution
Knowledge Check
Ball 1 collides with an another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of ball 2 becomes two times that of ball I after collision?
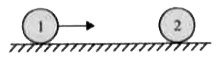 A13B12C14D16
A13B12C14D16A ball is dropped from a height h on a horizontal plane and the coefficient of restitution for the impact is e, the velocity with which the ball rebounds from the flor is
AehBeghCe√(gh)De√(2gh)A ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.
 Av=4m/sBv=3m/sCv=0m/sDv=1m/s
Av=4m/sBv=3m/sCv=0m/sDv=1m/s
A ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionA ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball of mass m moving with velocity u impinges on a ball of mass em moving with velocity eu in the opposite direction. If the impact be direct and e be the coefficient of restitution then the velocity of the second ball after impact is the same as that of the first ball before impact.
View Solution
