A solid cube of wood of side and mass is resting on a horizontal surface. The cube is constrained to rotate about an axis passing through and perpendicular to face . A bullet of mass and speed is shot at a height of as shown in the figure. The bullet becomes embedded in the cube. Find the minimum value of required to topple the cube. Assume .

Let be the angular velocity of cube just after collison about an axis passing through . From conservation of the angular mometum about an axis passing through .

Here
where perpedicular distance of axis of rotation passing through from centre of mass (com) of the cube
or
or
........i
The cube will topple if its is just able to reach in a vertical height as shown in figure.

Hence applying conservation of mechanical energy
(
or
or
or
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Knowledge Check
A solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure. The cube is free to rotate about the fixed axis AB. A bullet of mass m (<<M) and speed v is shot horizontally at the face opposite to ABCD at a height 'h' above the surface to impart the cube an angular speed ωc so that the cube just topples over. Then ωc is (note : the moment of inertia of the cube about an axis perpendicular to the face and passing through the center of mass is 2Ma3/3)
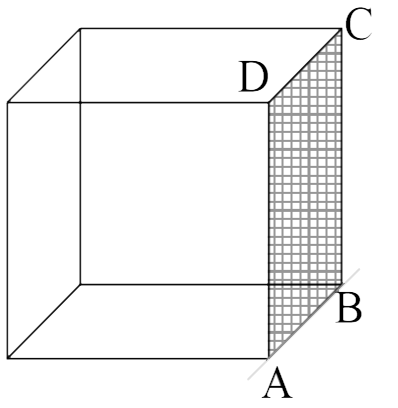 A√3gM/2maB√3g/4hC√3g(√2−1)/2aD√3g(√2−1)/4a
A√3gM/2maB√3g/4hC√3g(√2−1)/2aD√3g(√2−1)/4aA solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure. The cube is free to rotate about a fixed axis AB. A bullet of mass m (<<M) and speed v is shot horizontally at the face opposite to ABCD at a height 4a/3 from the surface to impart the cube an angular speed ω. It strike the face and embeds in the cube. Then ωc is close to (note : the moment of inertia of the cube about an axis perpendicular to the face and passing through the center of mass is 2Ma2/3)
 AMv/maBMv/2maCmv/MaDmv/2Ma
AMv/maBMv/2maCmv/MaDmv/2MaA solid cube of side 2a and mass M, sliding on a smooth surface with velocity v0 , collides inelastically with the raised edge of the table:
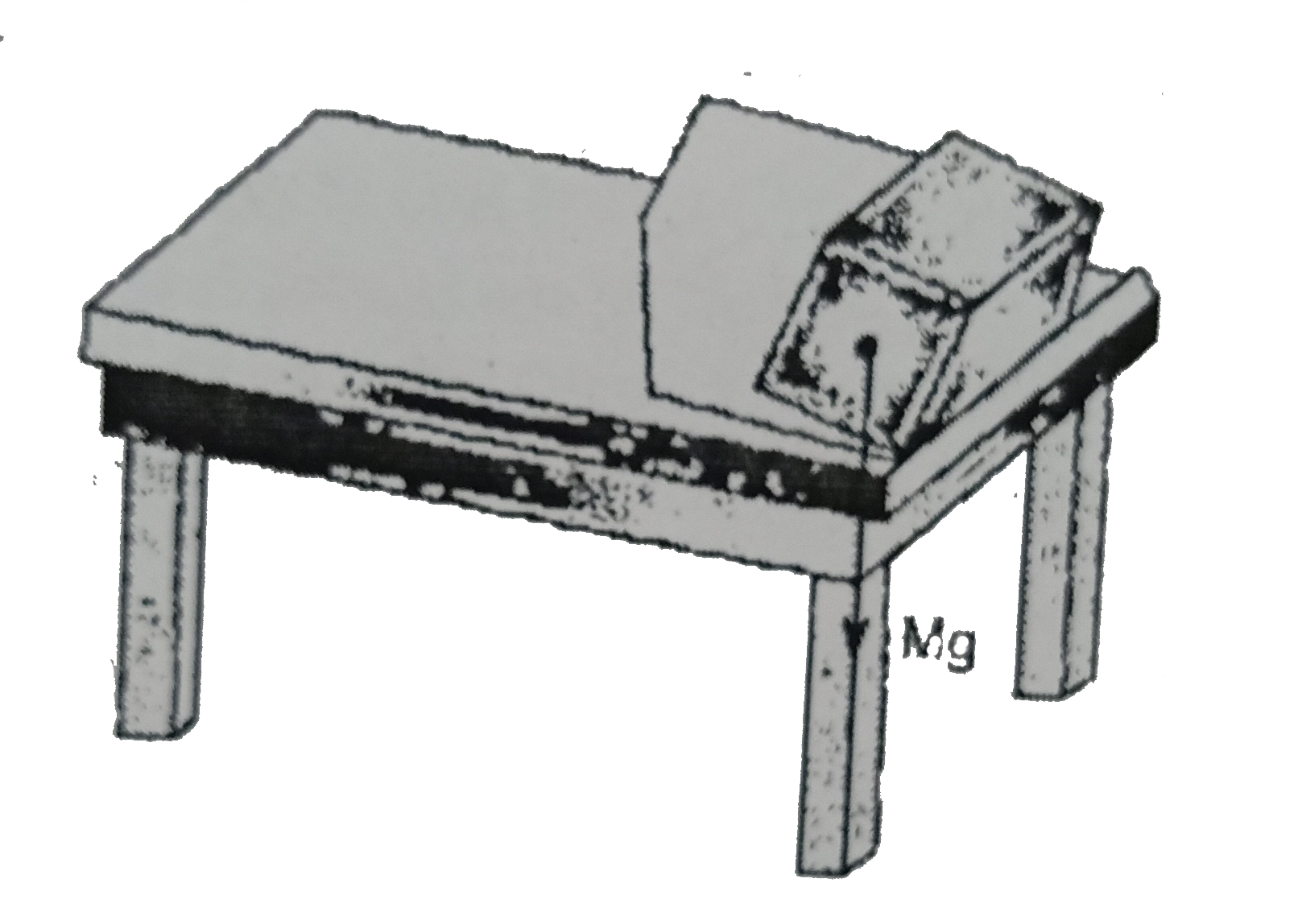 AMoment of inertia of cube about edge is 4Ma23BMoment of inertia of cube about edge is 8Ma23CMinimum value of v so that cube falls off the table is √1.19gDEnergy of system is conserved
AMoment of inertia of cube about edge is 4Ma23BMoment of inertia of cube about edge is 8Ma23CMinimum value of v so that cube falls off the table is √1.19gDEnergy of system is conserved
Figure shows a cubical wooden block of side length a and mass M which is resting over a horizontal surface and constrained to rotate about its right lower edge D. A bullet of mass m moving horizontally, directly towards its centre with velocity v strikes and gets embedded in it. During subsequent motion the block just topples, calculate v. Assume m<<M.
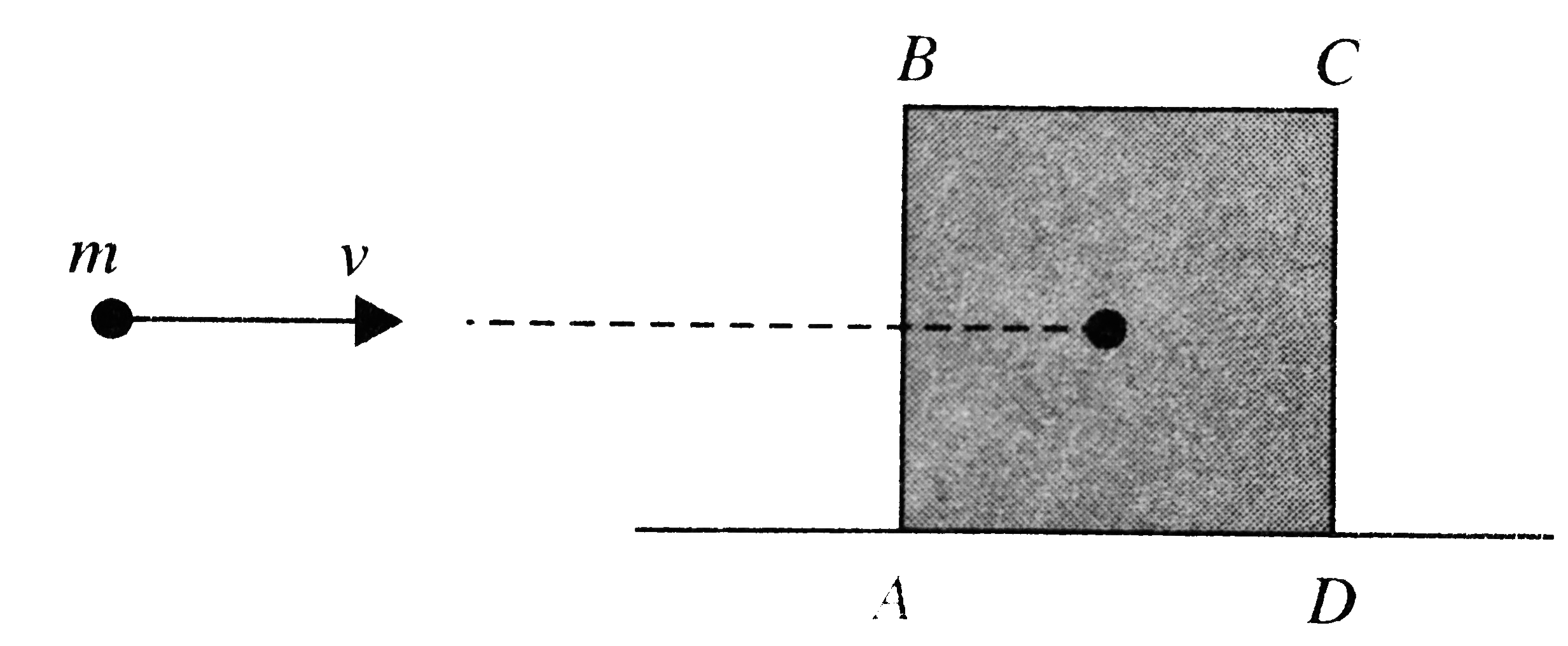
View SolutionFigure shows a cubical wooden block of side length a and mass M which is resting over a horizontal surface and constrained to rotate about its right lower edge D. A bullet of mass m moving horizontally, directly towards its centre with velocity v strikes and gets embedded in it. During subsequent motion the block just topples, calculate v. Assume m<<M.

View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionFrom a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
View Solution

