A hoop of mass is projected on a floor with linear velocity and reverse spin . The coefficient of friction between the hoop and the ground is .
a. Under what condition will the hoop return back?
b. How far will it go?
c. How long will it continue to slip when its centre of mass becomes stationary?
d. What is the velocity of return?
The correct Answer is:
a.The acceleration of the hoop,
Angular acceleration of the wheel
Linear velocity at time
………..i
Angular velocity at time ,
………ii
Let linear velocity be zero at . So,
or
Angular velocity of the at ring at is
............iii
The hoop will return if it has reverse spin at the instant its linear velocity is zero. So the condition for hoop to return is
or
b. Distance moved by the hoop
c. Let be the time flow during which the hoop slips on the floor and be the return velocity.
Then
and
No slip conditon is achieved when
From Eq. iii
or
d.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
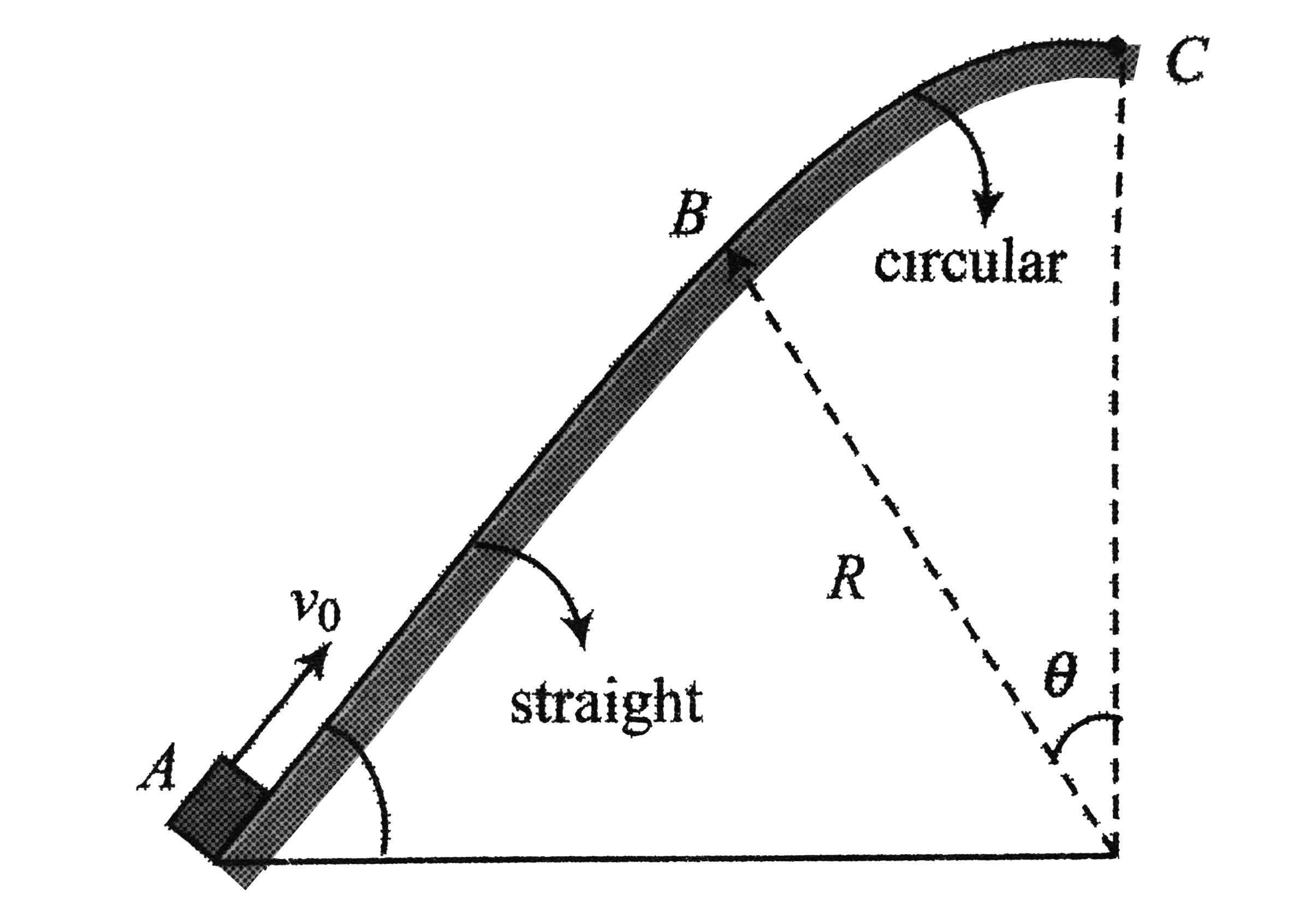
A block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
View SolutionA small block of mass m is projected on a larger block of mass 10m and length l with a velocity v as shown in the figure. The coefficient of friction between the two block is μ2 while that between the lower block and the ground is μ1. Given that μ2>11μ1.

(a) Find the minimum value of v, such that the mass m falls off the block of mass 10m .
(b) If v has minimum value, find the time taken by block m to do so.
View Solution
Knowledge Check
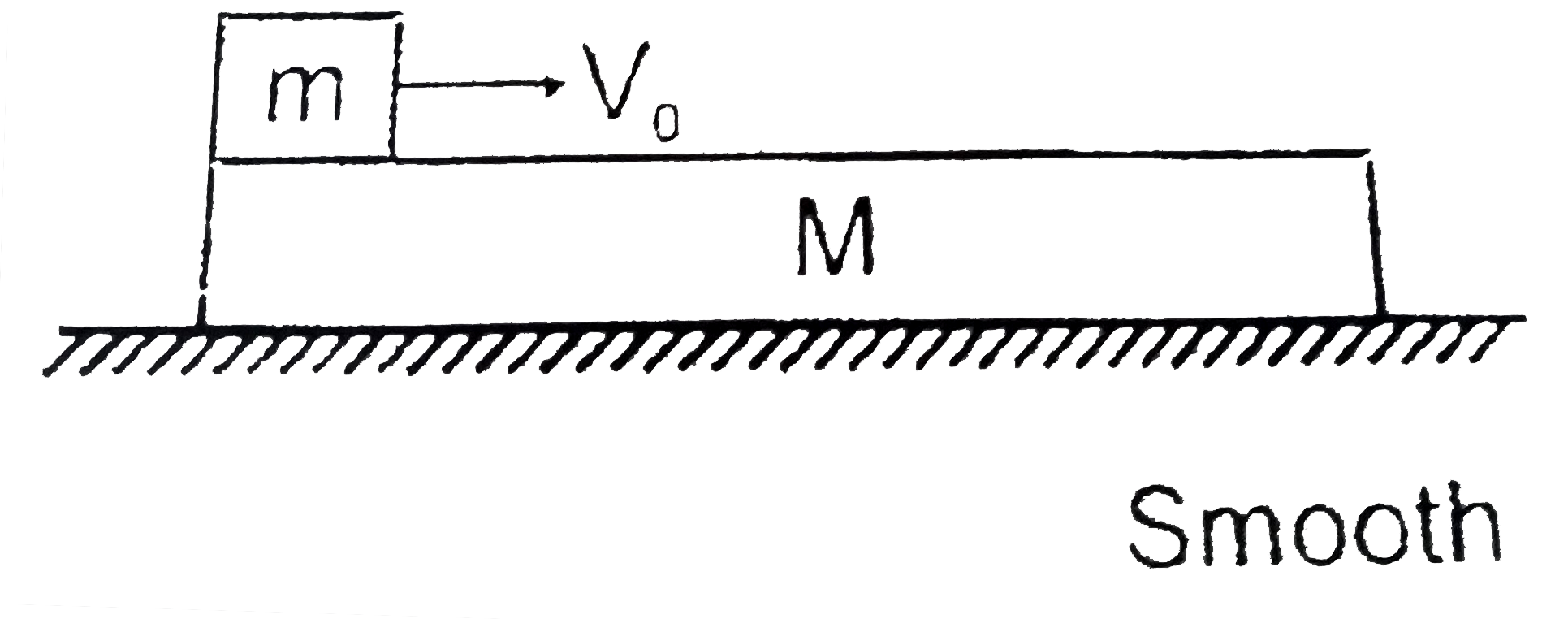
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:AThe work done b friction on the block is negativeBthe work done by friction on the plank is positiveCthe net work done by friction is negativeDnet work done by the friction is zero.A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB227ω20r2μgC481ω20r2μgD281ω20r281μgA block mass m=2kg is moving with velocityv0 towards a massless unstretched spring of the force constant k=10N/m. Coefficient of friction between the block and the ground is μ=0.2. Find the maximum value of v0 so that after pressing the spring the block does not return back but stops there permanently.
 A2√25m/sB√15m/sC4√15m/sD4√25m/s
A2√25m/sB√15m/sC4√15m/sD4√25m/s
A disc of radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4 (at t=0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ. The sense of rotation and direction of its linear speed are shown in the figure. The disc returns to its initial point in time T=256kμgω0R. Find the value of k.
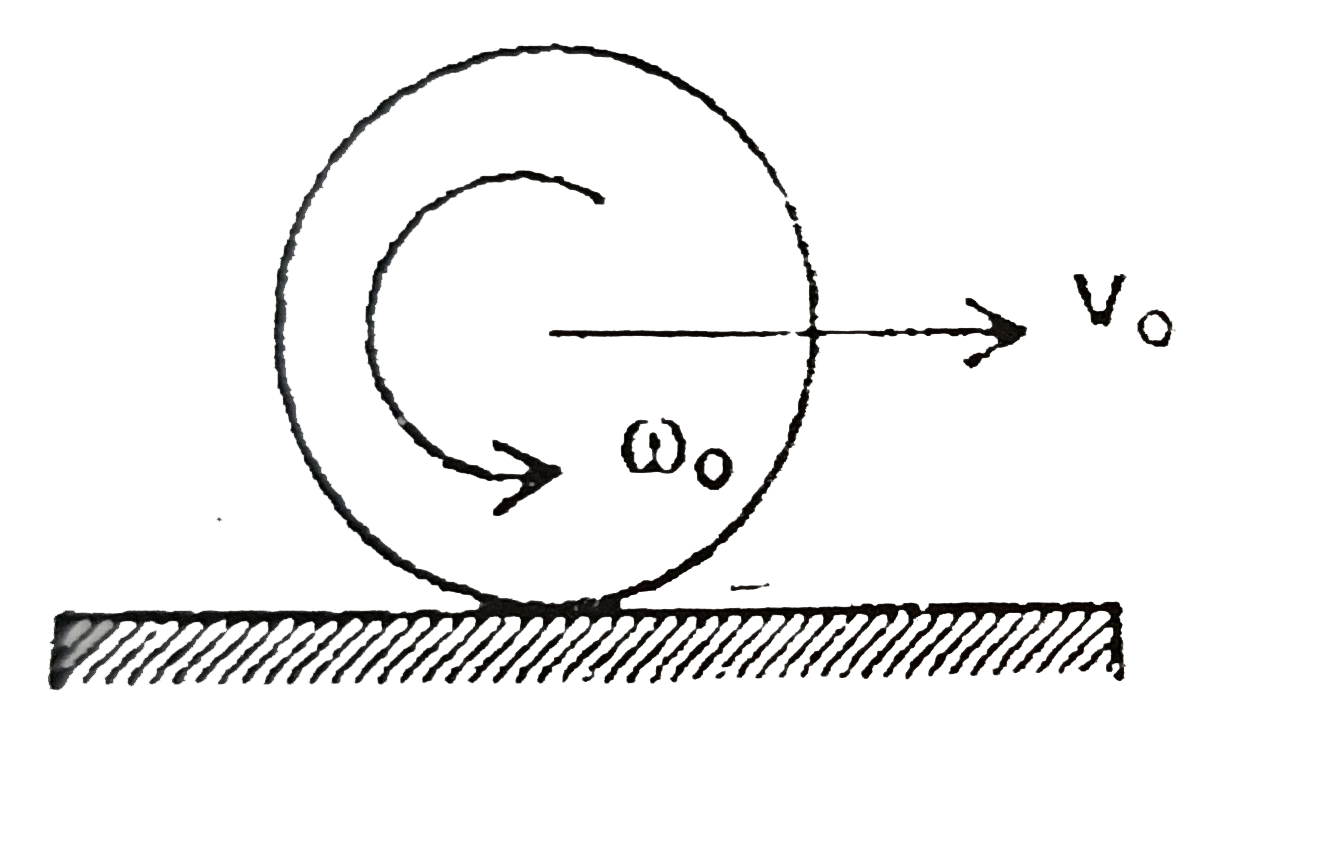
View SolutionA block of mass m=0.14kg is moving with velocity v0 towards a mass less unstretched spring of force constant K=10Nm−1. Coefficient of friction between the block and the ground is μ=1/2.
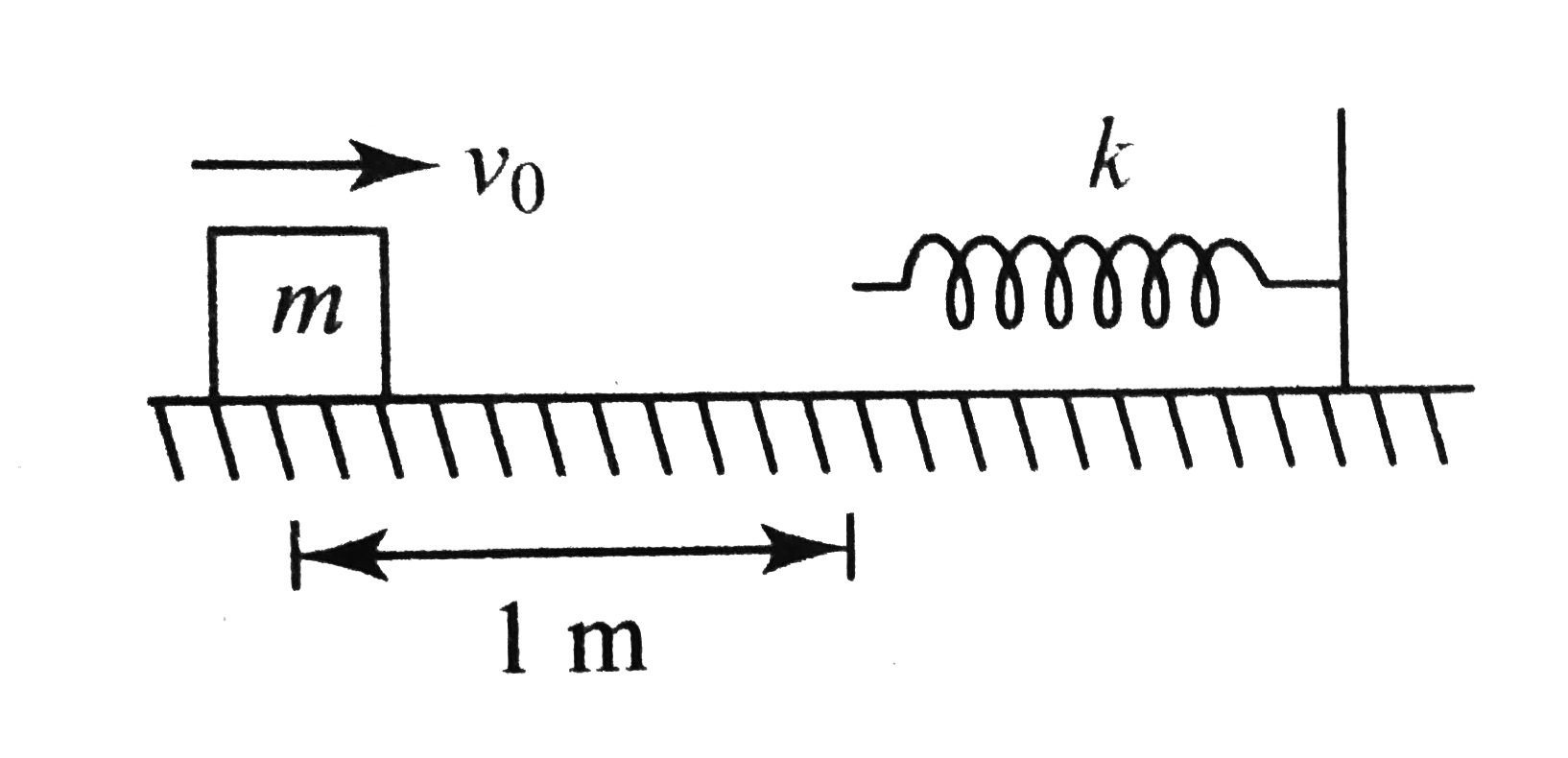
Find the maximum value of compression in the spring (in cm), so that after pressing the spring the block does not return back but stops there permanently.
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
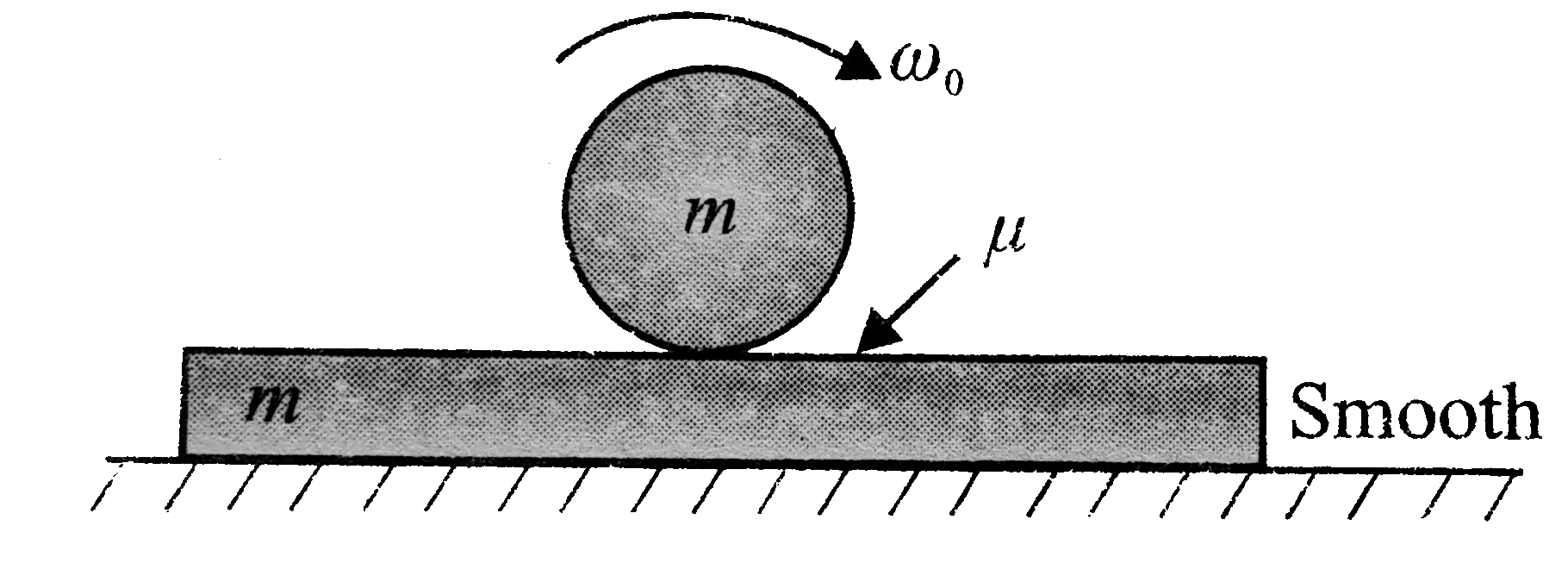
Find the velocity of the sphere after the pure rolling starts
View SolutionOn a stationary block of mass 2kg a horizontal forces F starts acting at t=0 whose veriation with time is shown in figure .The coefficient of friction between the block and ground is 0.5 New answer the following question
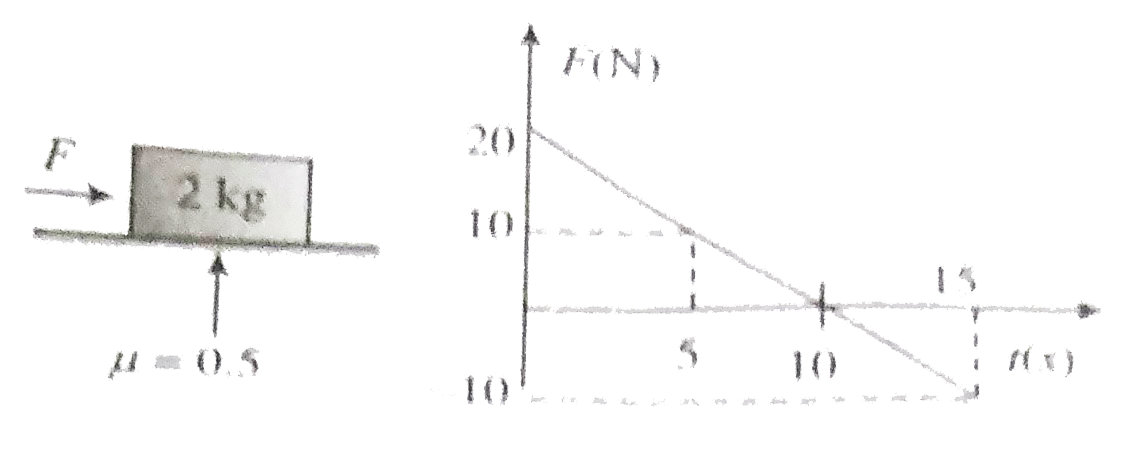
Find the velocity of the block when for the firsst time its acceleration become zero
View Solution