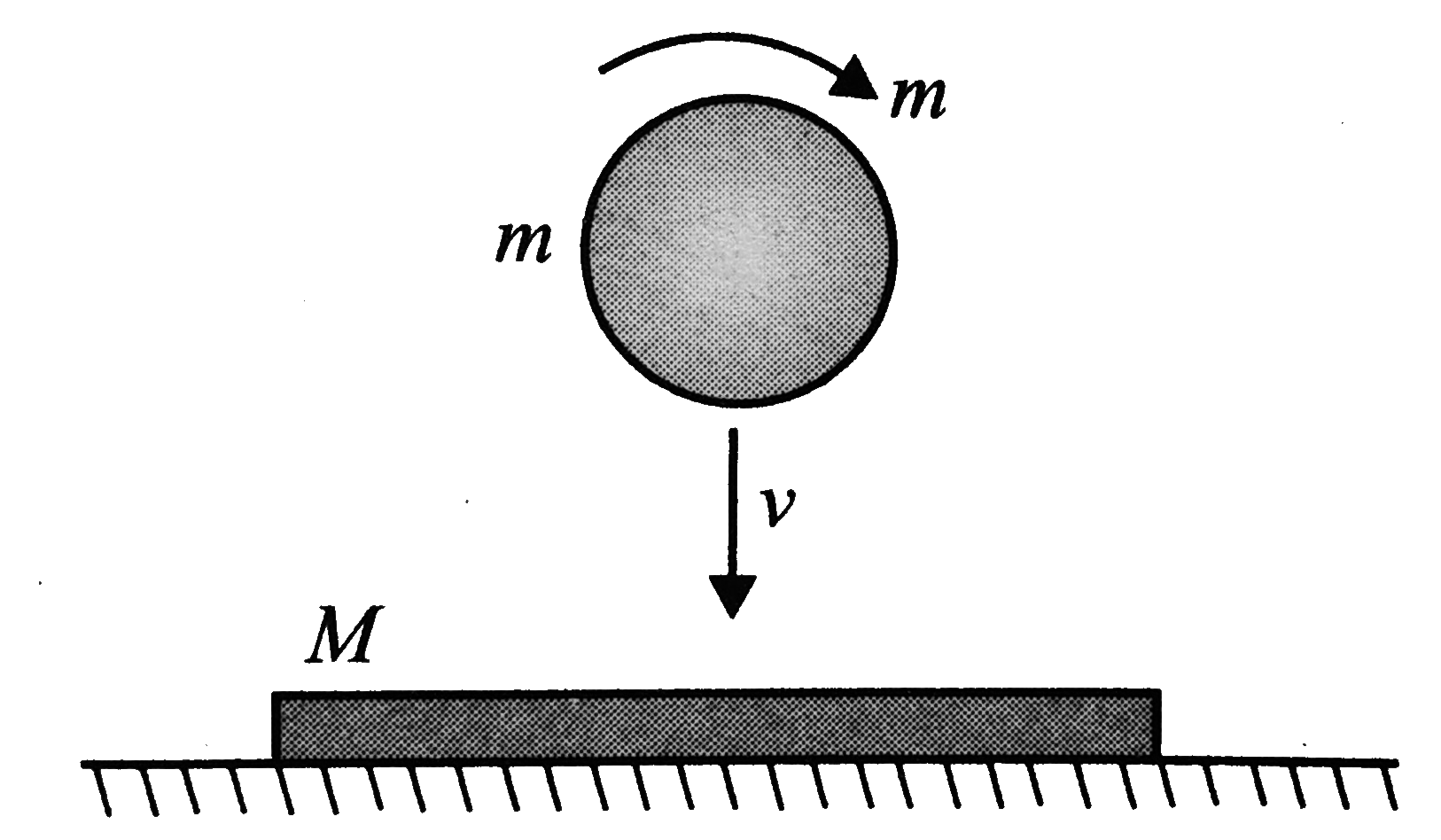
A solid ball of mass m and radius R spinning with angular velocity falls on a horizontal slab of mass M with rough upper surface (coefficient of friction ) and smooth lower surface. Immediately after collision, the normal component of velocity of the ball becomes half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given : ).

The correct Answer is:B
………….(i)
…………(ii)

From Eqs. (i) and (ii), we get
………(iii)
Let V and V1 be the speeds of the plank and the sphere, respectively, in the horizontal direction,
From Eqs. (i) and (iv), and
Similar Questions
A solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity (in m/s) of the sphere in horizontal direction immediately after the impact (given: Rω=5).
 View Solution
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg - Question 2 - Select One
A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
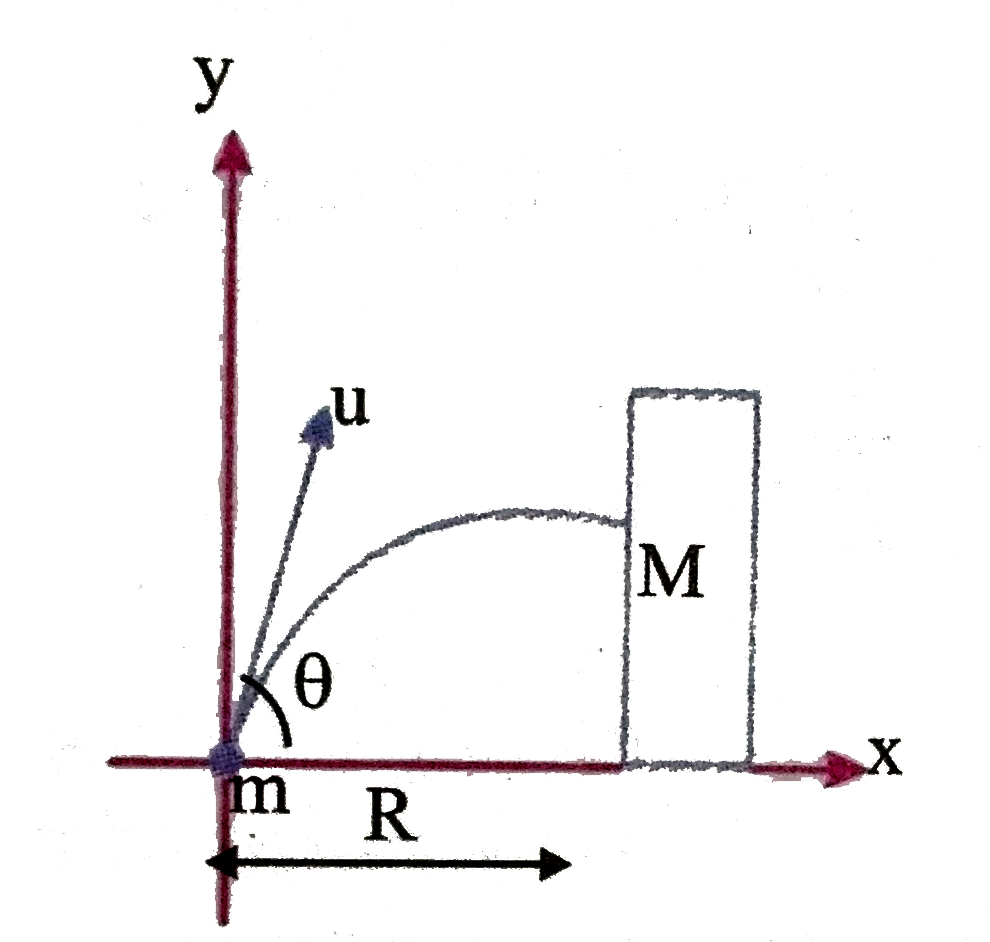
FInd the velocity of the ball after collisionA(m−eMM+m)ucosθB(M−emM+m)ucosθC(m+eMM+m)usinθD(m−eMM+m)usinθ - Question 3 - Select One
A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
Av1=(1−e)u2,v2=(1+e)u2Bv1=(1+e)u2,v2=(1−e)u2Cv1=u2,v2=−u2Dv1=(1+e)u,v2=(1−e)u
A solid sphere with angular velocity ω0 is dropped on a rough surface with coefficient of frication 'μ' froma height 'h'. If the collision with ground is perfectly inelastic if the velocity of centre of mass just after the impact is μ√xgh3 then value of x would be :
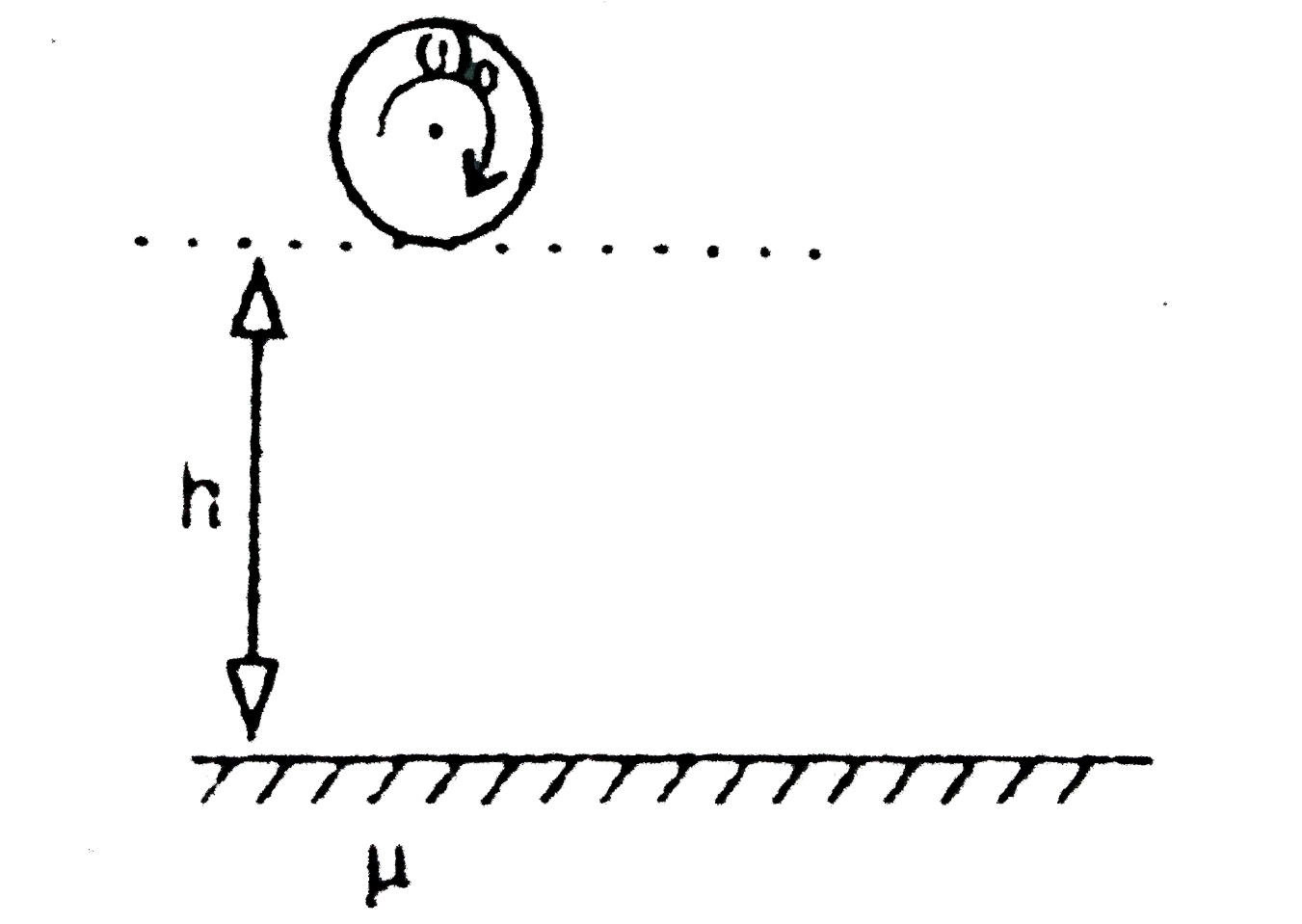 View Solution
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is component of the velocity of the block is √2gh , then θ is
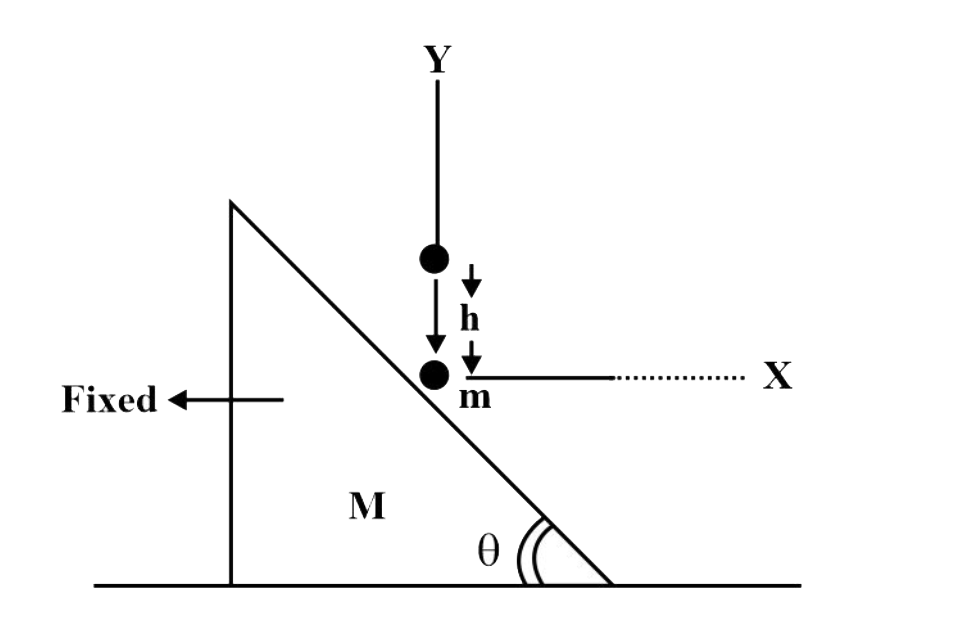 View Solution
View SolutionA solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
View SolutionA cylinder is rolling towards a cube of same mass on rough horizontal surface ( coefficient of friction = μ) with velocity v0 as shown in figure. Assume elastic collision and friction is negligible between cube and cylinder. Then after collision
 View Solution
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View Solution

