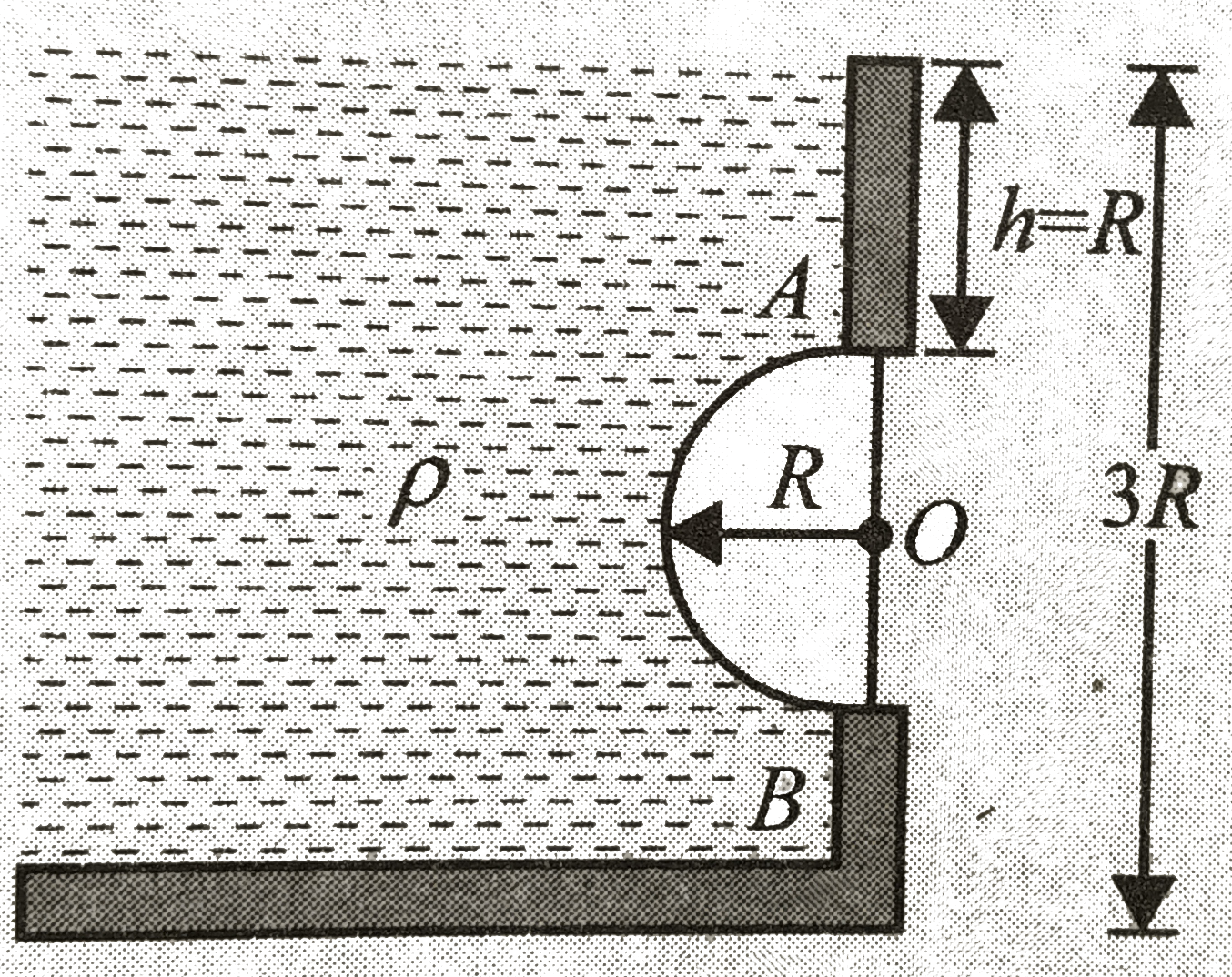
Figure shows a semi-cylindrical massless gate pivoted at the point O holding a stationary liquid of density ρ. The length of the cylinder is l. Calculate, the horizontal force exerted by the liquid on the gate.
4ρgR2l
ρgR2l
4ρgR3l
none
The correct Answer is:A
The force exerted by liquid on the gate is
fH=Pav×vertical projection area of the gate
=(PA−PB2)×(2Rl)
=(Rρg+3Rρg2)×2Rl=4ρgR2l
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.211videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.310videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples7videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
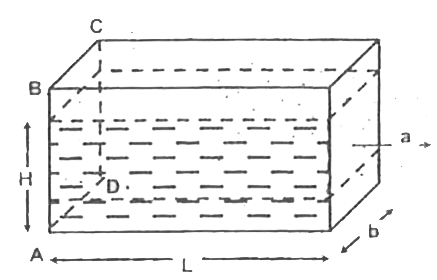
The force F needed to support the liquid of density ρ and the vessel on it, in figure, is
View SolutionA container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
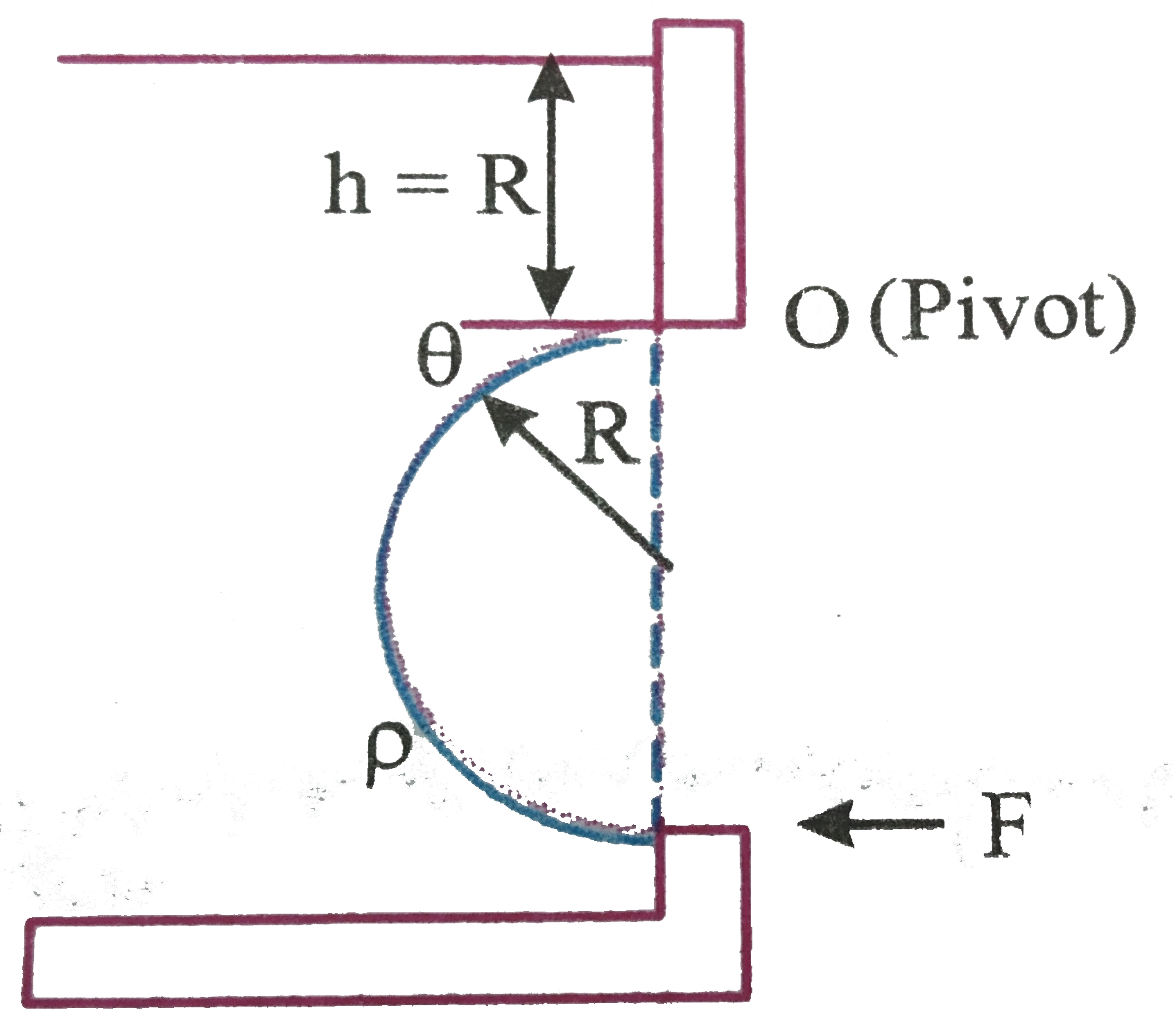
The fig shows a semo-cylinderical massless gate of unit length perpendicular to the plane of the page and is pivoted at the point O holding a stationary liquid of density ρ. A horizontal foce F is applied at its lowest position to keep it stationary. The magnitude of the force is:A32ρgR2B92ρgR2CρgR2D2ρgR2 - Question 2 - Select One
A light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to
 A2πR3ρgB2ρgR3C2R2ρg3DNone of these
A2πR3ρgB2ρgR3C2R2ρg3DNone of these - Question 3 - Select One or More
A liquid of density ρ comes out with a velocity v from a horizontal tube of area of cross-section A. The reaction force exerted by the liquid on the tube is F :
AF∝vBF∝v2CF∝ADF∝ρ
A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
View SolutionA light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to
 View Solution
View SolutionA square gate of size 1m×1m is hinged at its mid point. A fluid of density ρ fill the space to the left of the gate. The force F required to hold the gate stationary is
 View Solution
View SolutionA square gate of size 1m×1m is hinged at its mid point. A fluid of density ρ fill the space to the left of the gate. The force F required to hold the gate stationary is
 View Solution
View SolutionA square gate of size 1m×1m is hinged at its mid point. A fluid of density ρ fill the space to the left of the gate. The force F required to hold the gate stationary is
 View Solution
View Solution

