A square gate of size 1m×1m is hinged at its midpoint. A fluid of denisty ρ fills the space to the left of the gate. The force F required to hold the gate stationary is

ρg3
ρg2
ρg6
ρg8
The correct Answer is:C
At a depth y from tfhe surface of the fluid, the net force acting on the gate element of width dy is
dF=(p0+ρgy−p0)×1dy=ρgydy
Torque of this force about the hinge is
dtau=ρgydy×(12−y)
Net torque experienced by the gate is
τnet=∫τ+F×12
=∫10ρgydy(12−y)+F×12=0
⇒F=ρg6

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A square gate of size 4m x 4m is hinged at topmost point. A fluid of density ρ fills the space left of it. The force which acting 1m from lowest point can hold the gate stationary is?
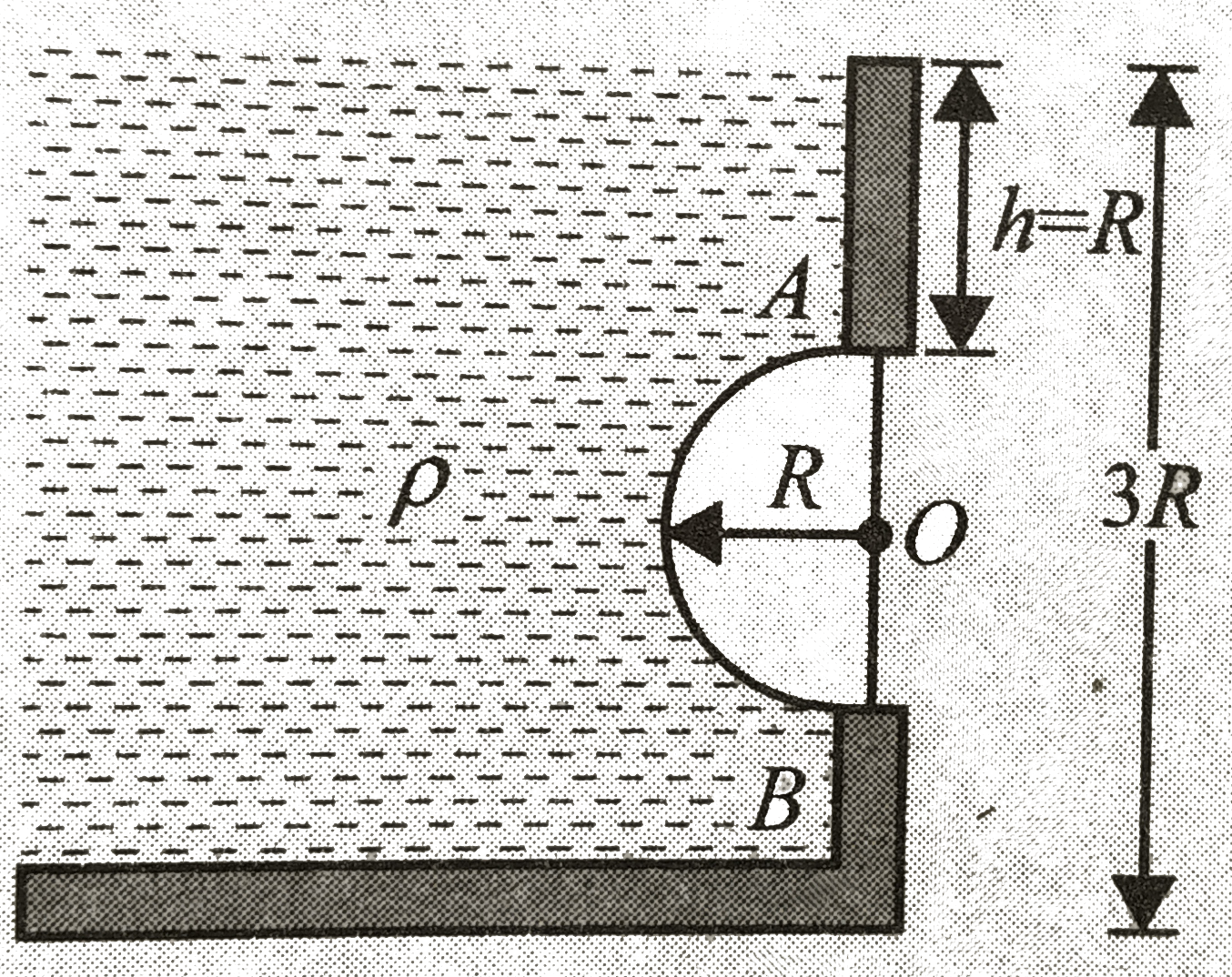
View SolutionA light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A square gate of size 1m×1m is hinged at its mid point. A fluid of density ρ fill the space to the left of the gate. The force F required to hold the gate stationary is
 Aρg3Bρg2Cρg6Dρg8
Aρg3Bρg2Cρg6Dρg8 - Question 2 - Select One
A square gate of size 1m×1m is hinged at its mid point. A fluid of density ρ fill the space to the left of the gate. The force F required to hold the gate stationary is
 Aρg6B12ρgCρg6DNone of these
Aρg6B12ρgCρg6DNone of these - Question 3 - Select One
A light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to
 A2πR3ρgB2ρgR3C2R2ρg3DNone of these
A2πR3ρgB2ρgR3C2R2ρg3DNone of these
Figure shows a semi-cylindrical massless gate pivoted at the point O holding a stationary liquid of density ρ. The length of the cylinder is l. Calculate, the horizontal force exerted by the liquid on the gate.
 View Solution
View SolutionIn Fig.7.125, coefficient of friction between m1 and m2 is μ and that between m1 and the wall is zero. A force F is pressing the system against the wall. Minimum value of force required to hold the system in equilibrium is :
View Solution
The fig shows a semo-cylinderical massless gate of unit length perpendicular to the plane of the page and is pivoted at the point O holding a stationary liquid of density ρ. A horizontal foce F is applied at its lowest position to keep it stationary. The magnitude of the force is:View Solution
A long capillary tube of mass π gm, radisu 2mm and negligible thickness, is partially immersed in a liquid of surface tension 0.1Nm. Take angle of contact zero and neglect buoyant force of liquid. The force required to hold the tube vertically, will be (g=10ms2)View SolutionA rope of length L and mass M is being pulled on a rought horizontal floor by a contact horizontal force F=mg. The force is acting at one end of the rope in the same direction as the length of the rop. The coefficient of kinetic friction between rope and floor is 1/2. Then the tension at the midpoint of the rop is
View Solution

