Young's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
Rs=√2RB
RS=RB√2
RS=4RB
RS=(RB)/4
The correct Answer is:B
To solve the problem, we need to relate the radii of the brass and steel wires given their Young's moduli and the fact that they are extended by the same amount under the same force.
1. Understanding Young's Modulus:
Young's modulus Y is defined as:
Y=F⋅L0A⋅ΔL
where:
- F is the force applied,
- L0 is the original length,
- A is the cross-sectional area,
- ΔL is the change in length.
2. Setting Up the Equations for Brass and Steel:
Let:
- YB=10×1010N/m2 (Young's modulus for brass),
- YS=2×1011N/m2 (Young's modulus for steel),
- RB = radius of the brass wire,
- RS = radius of the steel wire.
Since both wires are extended by the same amount (ΔL=1mm=0.001m), we can write the equations for the two wires:
ΔL=F⋅L0AB⋅YB(for brass)
ΔL=F⋅L0AS⋅YS(for steel)
3. Cross-Sectional Area:
The cross-sectional area A for a wire with radius R is given by:
A=πR2
Therefore, we can rewrite the equations as:
ΔL=F⋅L0πR2B⋅YB
ΔL=F⋅L0πR2S⋅YS
4. Equating the Two Expressions:
Since ΔL is the same for both wires, we can set the two expressions equal to each other:
F⋅L0πR2B⋅YB=F⋅L0πR2S⋅YS
5. Simplifying the Equation:
Canceling F and L0 from both sides and π as well, we get:
1R2BYB=1R2SYS
Rearranging gives:
R2SR2B=YBYS
6. Substituting Values:
Substitute the values of YB and YS:
R2SR2B=10×10102×1011=1020=12
7. Finding the Relationship Between Radii:
Taking the square root of both sides:
RSRB=1√2
Therefore, we can express RS in terms of RB:
RS=RB√2
Final Answer:
The radius of the steel wire RS is equal to RB√2.
Young's modulus Y is defined as:
Y=F⋅L0A⋅ΔL
where:
- F is the force applied,
- L0 is the original length,
- A is the cross-sectional area,
- ΔL is the change in length.
Let:
- YB=10×1010N/m2 (Young's modulus for brass),
- YS=2×1011N/m2 (Young's modulus for steel),
- RB = radius of the brass wire,
- RS = radius of the steel wire.
ΔL=F⋅L0AB⋅YB(for brass)
ΔL=F⋅L0AS⋅YS(for steel)
The cross-sectional area A for a wire with radius R is given by:
A=πR2
Therefore, we can rewrite the equations as:
ΔL=F⋅L0πR2B⋅YB
ΔL=F⋅L0πR2S⋅YS
Since ΔL is the same for both wires, we can set the two expressions equal to each other:
F⋅L0πR2B⋅YB=F⋅L0πR2S⋅YS
Canceling F and L0 from both sides and π as well, we get:
1R2BYB=1R2SYS
Rearranging gives:
R2SR2B=YBYS
Substitute the values of YB and YS:
R2SR2B=10×10102×1011=1020=12
Taking the square root of both sides:
RSRB=1√2
Therefore, we can express RS in terms of RB:
RS=RB√2
The radius of the steel wire RS is equal to RB√2.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct17videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning13videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective16videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
Knowledge Check
- Question 1 - Select One
The Young's modulus of brass and steel are 10×1010Nm−2and20×1010Nm−2 respectively. A brass wire and steel wire of the same length are extended by 1 mm under the same force. If the radii of the brass and steel wires are RBandRS respectively, then
ARS=RB4BRS=4RBCRS=√2,RBDRS=RB√2 - Question 2 - Select One
The young 's modulus of brass and steel are 1.0×1011Nm−2 and 2.0×1011N/m2. Respectively . A brass wire and steel wire of the same length extend by 1 mm, each under the same forece . It radii of brass and steel wires are RB and RS respectively, them
ARs=√2RBBRs=RB√2CRs=4RBDRS=RB2 - Question 3 - Select One
The Young's modulus of brass and steel are respectively 1.0×1011Nm−2 and 2.0×1011Nm−2. A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of brass and steel wires are RB and Rs respectively, then
ARs=√2RBBRs=RB√2CRs=4RBDRs=RB2
A block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
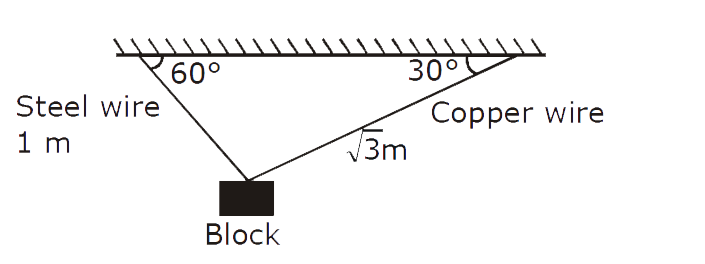
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
View SolutionThe Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
View SolutionIf young's modulus of steel is 2×1011N/m2, then the force required to increase the length of a wire of cross section 1cm2 by 1% will be
View SolutionIf the interatomic spacing in a steel wire is 2.8×10−10m. And Ysteel=2×1011N/m2,then force constant in N//m is
View Solution

