Draw g' versus dandg versus h graph. Here, d is depth below the surface of earth and h is the height from the surface of earth.
The variation of g with height h is related by g∝ar2 where r=R+h, i.e. part AB of the graph in the figure.
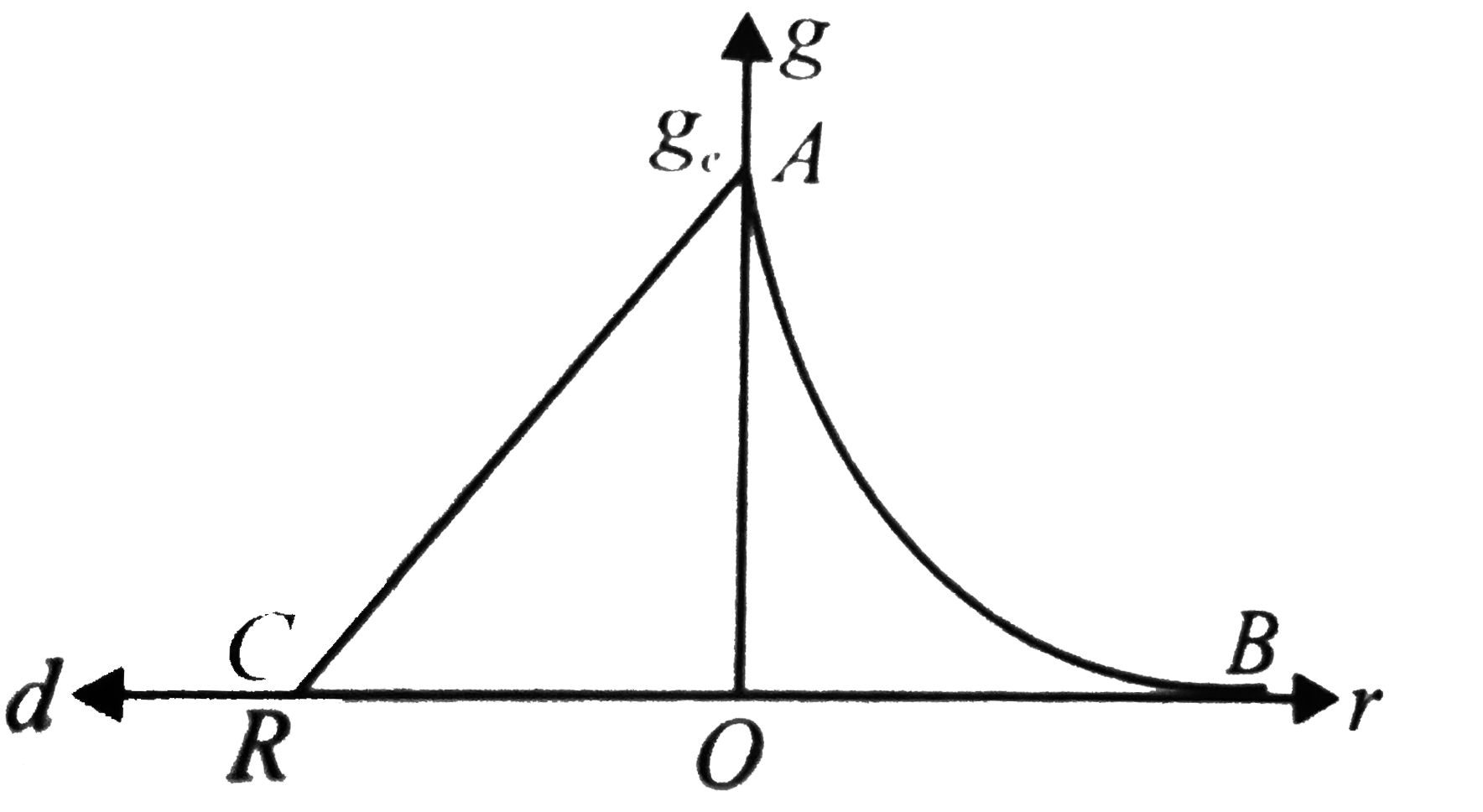
b. The varitation of g with depth is related by g'=g(1−dR) i.e., g∝(R−d). Thus the variation of g and d is a straigt line i.e., part AC of the graph in the figure.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Exercise 6.316videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Exercise 6.416videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Exercise 6.113videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
Knowledge Check
- Question 1 - Select One
The ratio of accleration due to gravity at a depth h below the surface of earth and at a height h above the surface of earth for h << radius of earth:
AIs constantBChanges linearly with hCChanges parabolically with hDDecreases - Question 2 - Select One
The graph that represents variation of g with height (h) from the surface of the earth is
A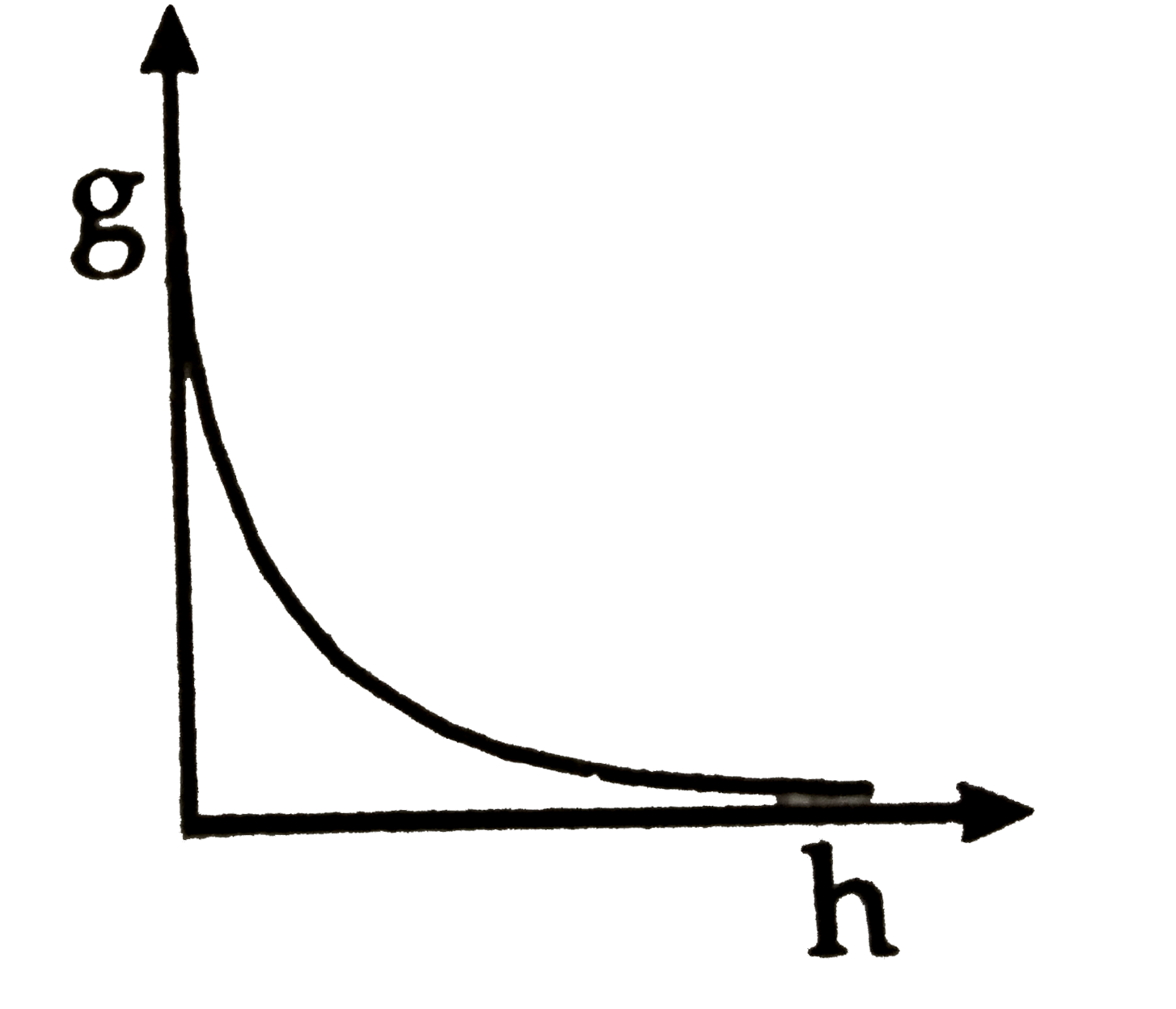 B
B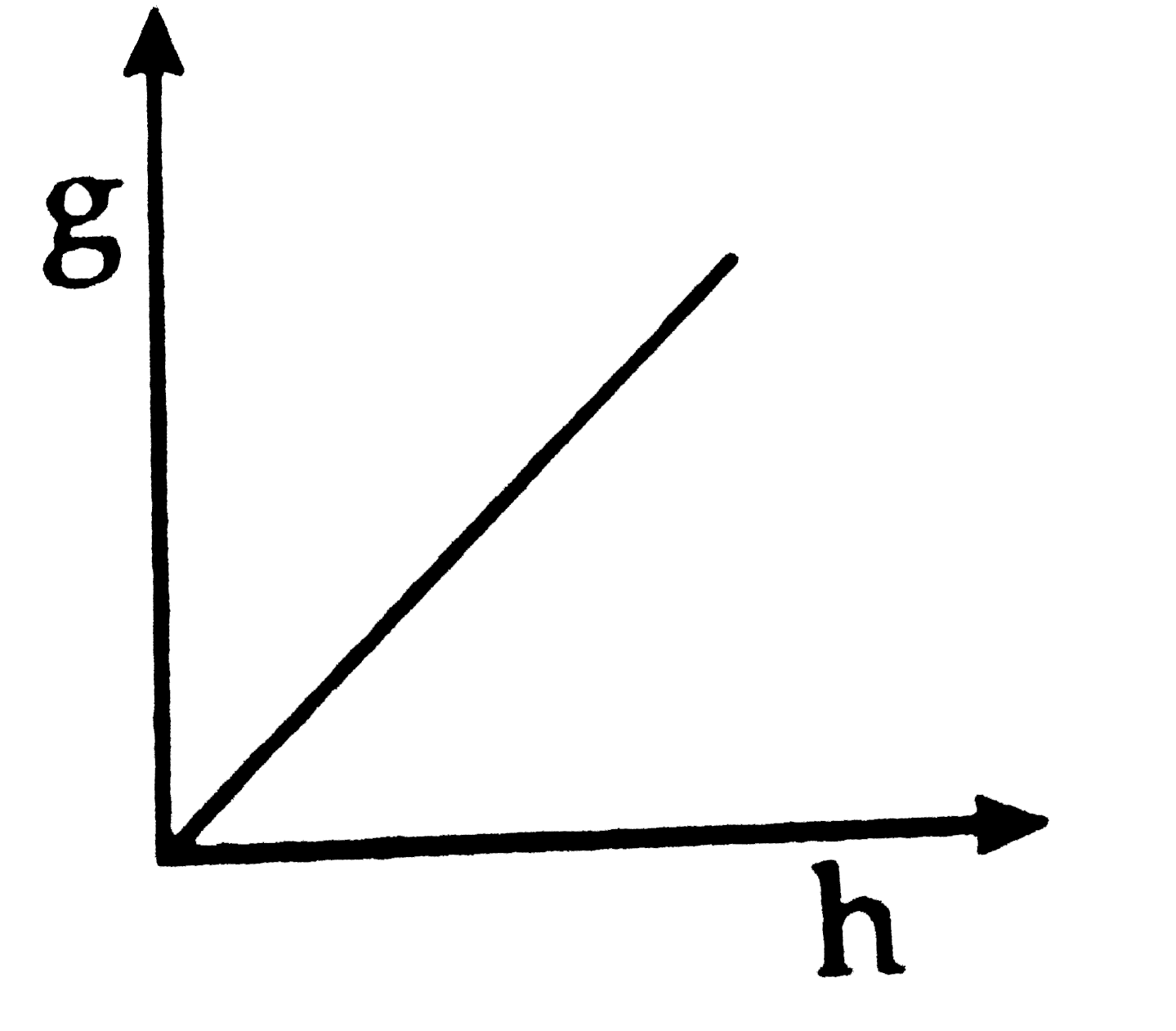 C
C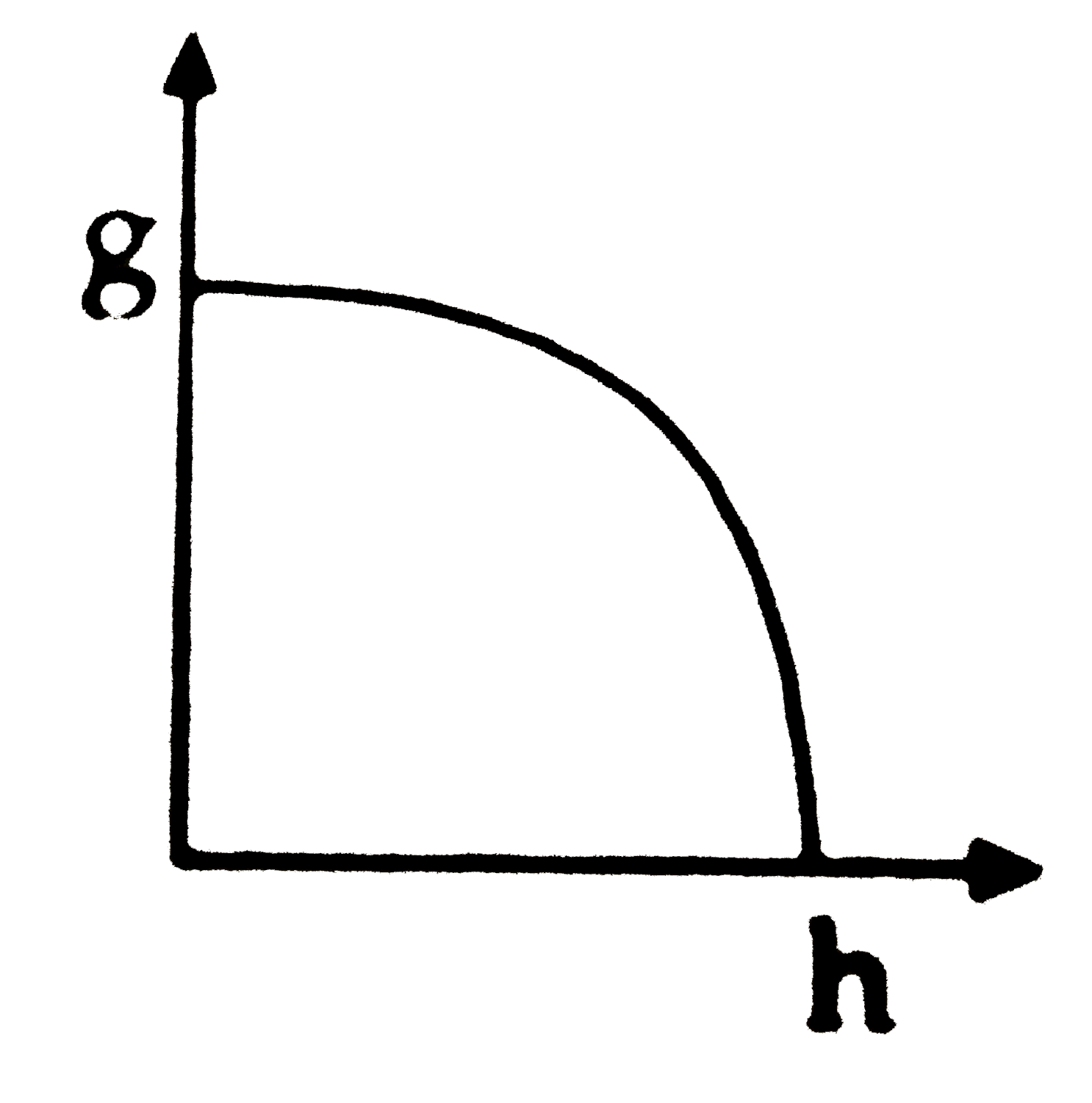 D
D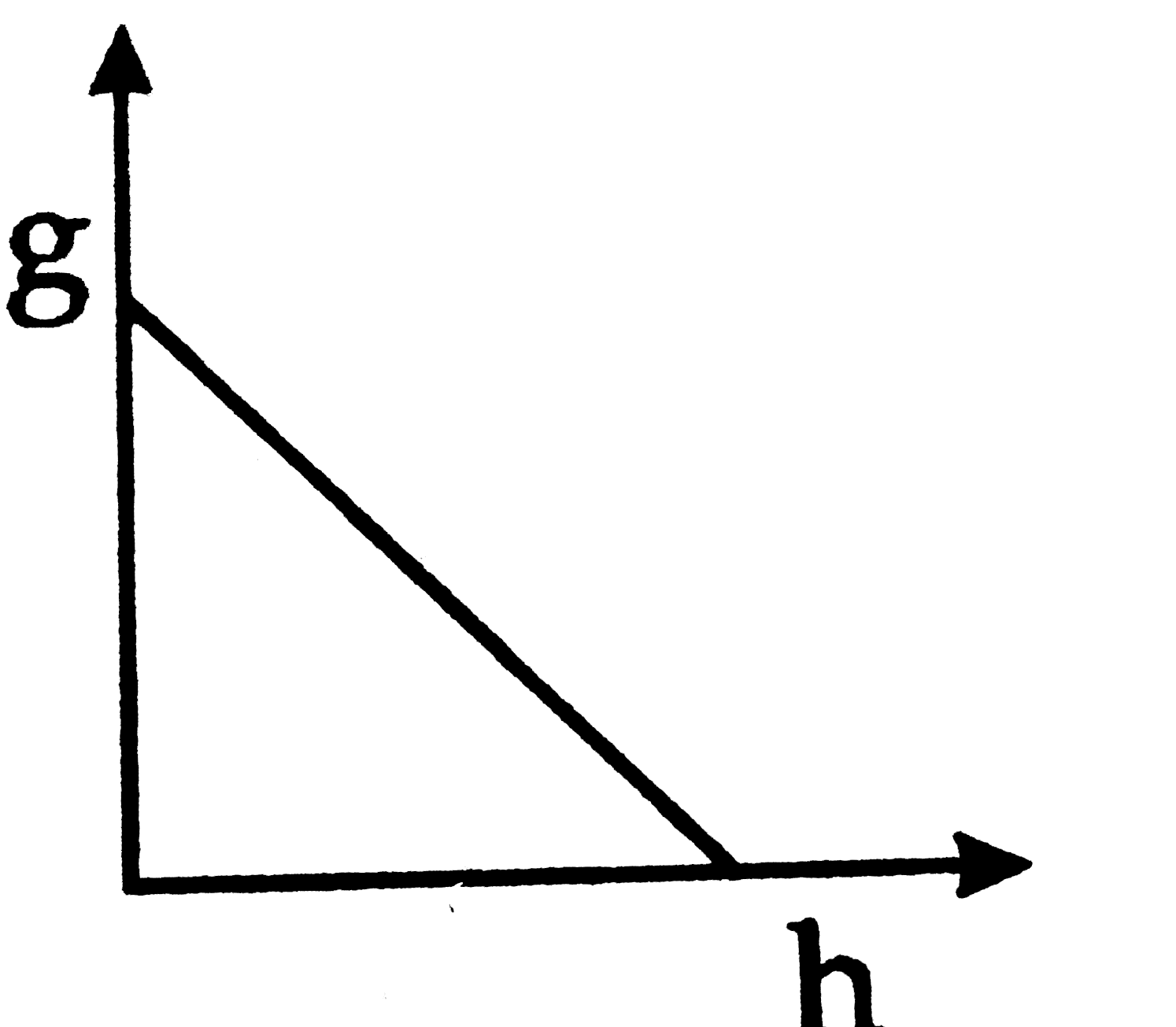
- Question 3 - Select One
At what depth below the surface of the earth, is the value of g same as that at a height of 10km from the surface of the earth?
A5kmB10kmC20kmD40km
Derive an expression for the variation of g with the height from the surface of Earth.
View SolutionDerive an expression for the variation of g with the height from the surface of the Earth.
View SolutionAt what depth below the surface of the earth, is the value of g same as that of a height of 5 km ?
View SolutionThe orbital velocity of a satellite is given by the expression V=sqrt((GM)/(R + h)), here M is the mass of the Earth, R is the radius of the Earth and 'h' is the height of the satellite from the surface of the Earth. Explain the reasons why the geostationary satellite is not possible to set in orbit around the Earth at two different heights from the surface of the Earth.
View SolutionThe height from the surface of earth and electron density of D layer of earth's atmosphere are
View Solution

