Question

State Kirchhoff's law for an electrical network. Using these laws deduce the conditions for balance in a wheatstone bridge.

Explanation

Kirchhoff's first law (junction rule or KCL) : The algebraic sum of the currents at any junction is zero `:. sum I = 0`
or
The sum of the currents flowing towards a junction is equal to the sum of currents away from the junction.
(2) Kirchhoff's second law (Loop rule or KVL) : The algebraic sum of potential around any closed loop is zero.
`:. sum (IR) + sum E = 0`
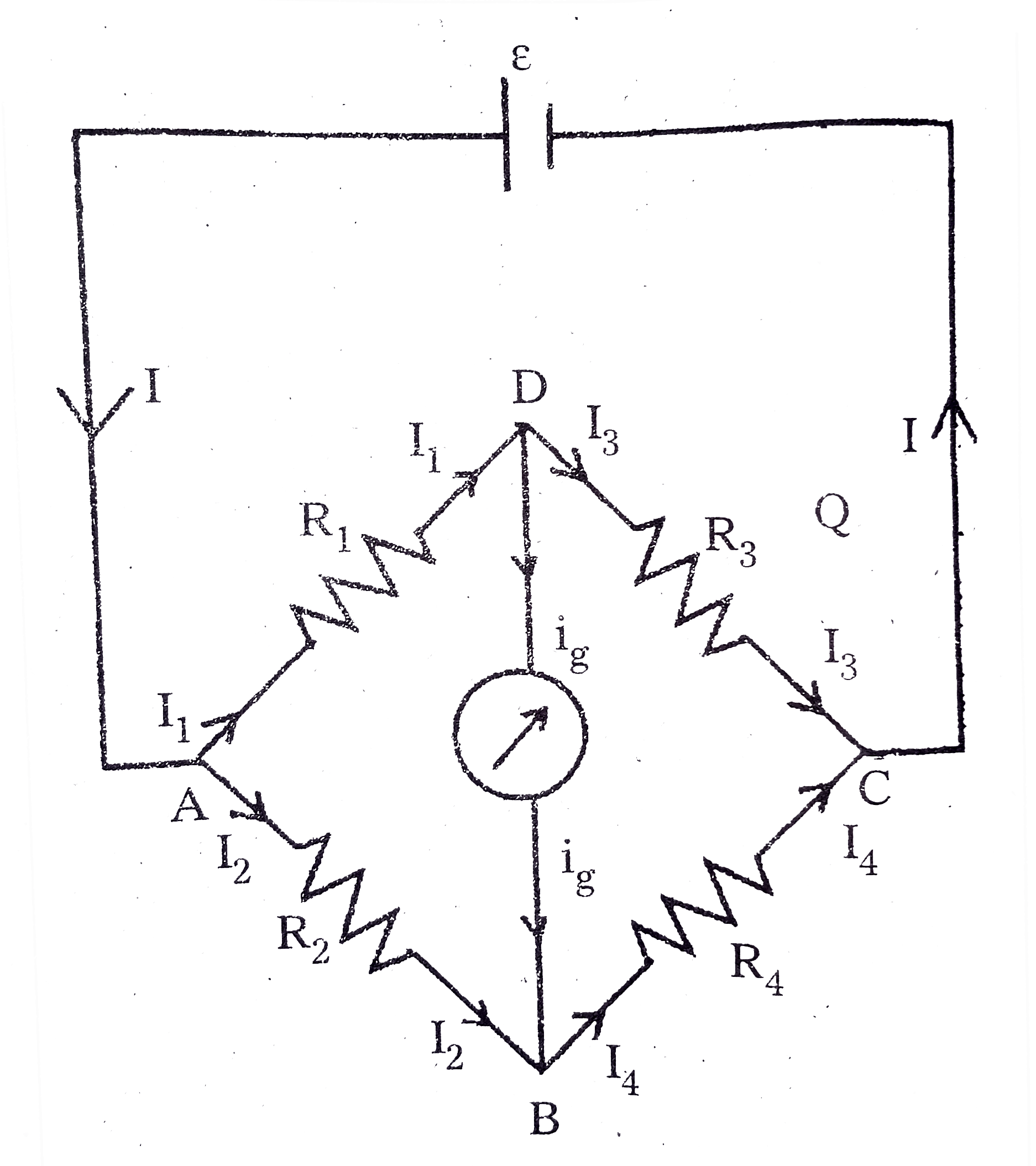
Wheatstone bridge : Wheatstone bridge consists of four resistances `R_(1), R_(2), R_(3)` and `R_(4)` are connected to form a closed path. A cell of emf `epsilon` is connected between the point A and C and a galvanometer is connected between the points B and D as shown in fig. The current through the various branches are indicated in the figure. The current through the galvanometer is `I_(g)` and the resistance of the galvanometer is G.
Applying Kirchhoff's first law
at the junction `D, I_(1) - I_(3) - I_(g) = 0`....(1)
at the junction `D, I_(2) + I_(g) 0 I_(4) = 0` ....(2)
applying Kirchhoff's second law to the closed path ADBA,
`-I_(1) R_(1) - I_(g) G + I_(2) r_(2) = 0`
or
`implies I_(1) R_(1) + I_(g) G = I_(2) R_(2)`....(3)
gt applying kirchhoff's second law to the closed path DCBD,
`- I_(3) R_(3) + I_(4) R_(4) + i_(g) G = 0`
`implies I_(2) R_(3) -I_(g) G - I_(4) R_(4)` .....(4)
When the galvanometer shows zero diflection the points D and B are at the same potential. So `I_(g) = 0`.
Substituting this value in (1),(2),(3) and (4)
`{:(I_(1) = I_(3), - , (5)),(I_(2) = I_(4), - , (6)),(I_(1) R_(1) = I_(2) R_(2), - , (7)),(I_(3) R_(3) = I_(4) R_(4), - , (8)):}`
Dividing (7) by (8)
`(I_(1) R_(1))/(I_(3)R_(3)) = (I_(2) R_(2))/(I_(4) R_(4)) implies (R_(1))/(R_(3)) = (R_(2))/(R_(1)) [ :' I_(1) = I_(3) & I_(2) = I_(4)]`
`:.` Wheatstone's Bridge principle : `R_(4) = R_(3) xx (R_(2))/(R_(1))`