Question

Use Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius $R$.
Draw the magnetic field lines due to circular wire carrying current $I$.

Explanation

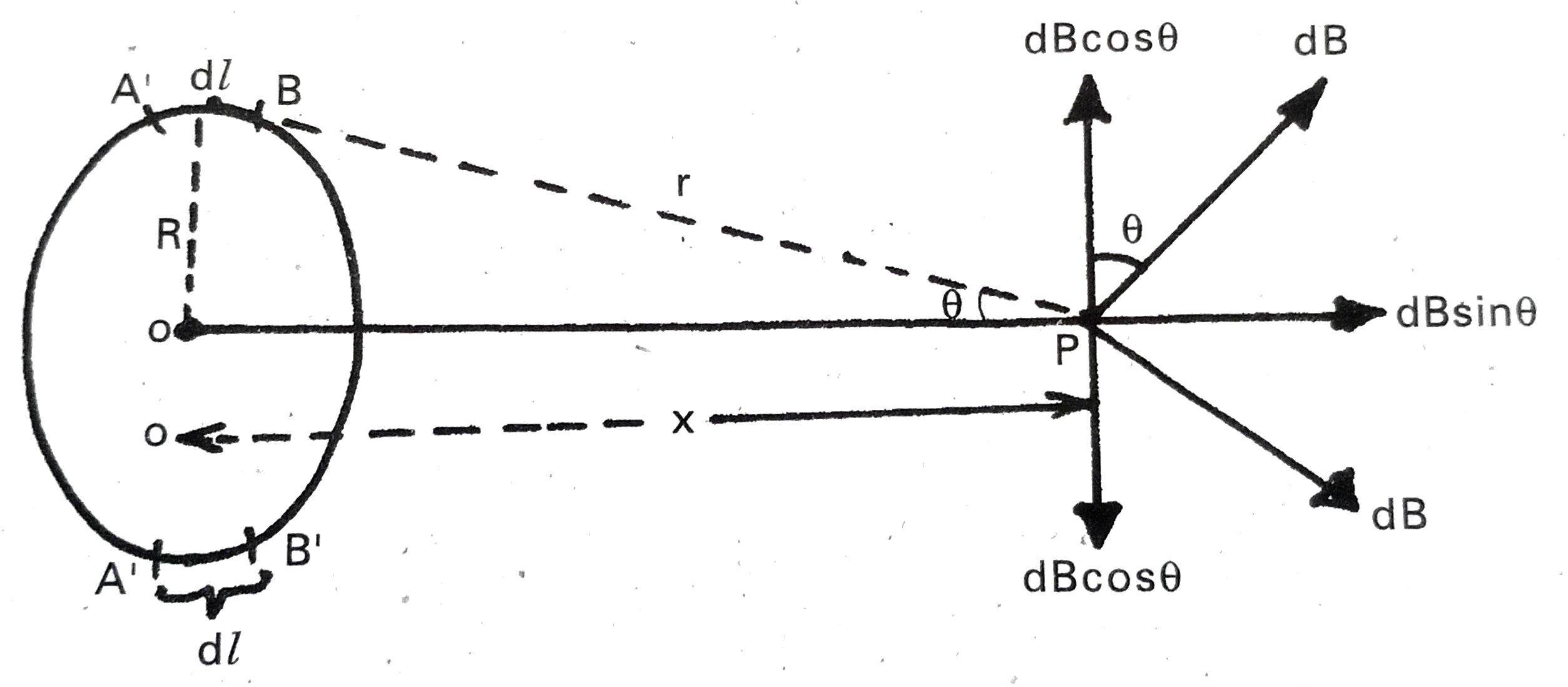
Consider a ciruclar coil of radius R and carrying a current i. Let P is a point on the axis at a distance x from the centre O. Let r be the distance of small element (dl) from P. From Biot-savart's law
`dB=(mu_(0))/(4pi)(I dl sin theta)/(r^(2))=(mu_(0))/(4pi). (idl)/(r^(2))rarr(1)" "(because theta =90^(@)" Angle between "vec(dl) and vecr)`
dB can be resolved into two components dB `cos theta and dB sin theta.` If we consider another element diametrically opposite to AB. This also resolved into dB `cos theta and dB sin theta.` The components along the axis will add up and perpenduclar to the axis will cancel.
`therefore` Resultant magnetic induction at P is
`B= int dB sin theta rarr (2)`
`B= int (mu_(0))/(4pi). (idl sin theta)/(r^(2))`
`=(mu_(0)i)/(4 pi r^(2)) int dl sin theta" "(because sin theta =(R)/(r))`
`=(mu_(0)i)/(4pi r^(2))xx2pi Rxx (R)/(r)" "(because int d l = 2pi R)`
`B=(mu_(0)i R^(2))/(2 r^(3))rarr(3)`
From figure `r=sqrt(R^(2)+x^(2))`
`B=(mu_(0)i R^(2))/(2(R^(2)+x^(2))^(3//2)) rarr (4)`
If the coil contains N turns,
`B=(mu_(0)Ni R^(2))/(2(R^(2)+X^(2)))^(3//2)rarr(5)`