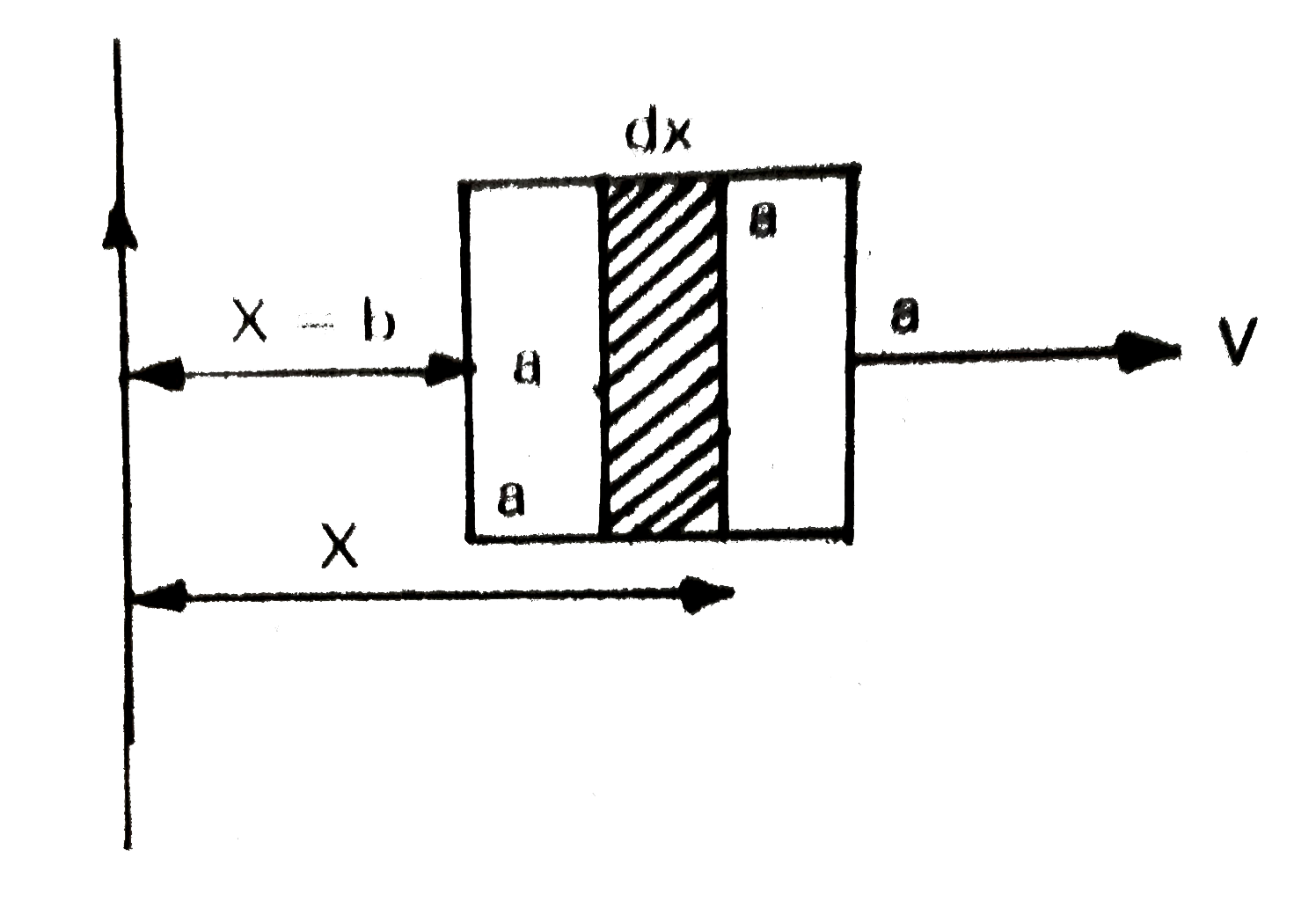
Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in the figure.  Solution in Telugu
Solution in Telugu
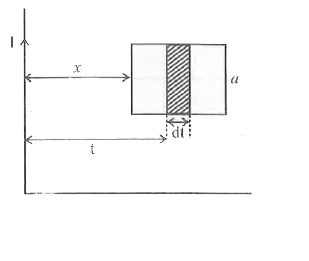
Let us assume that an elementary strip of width dx a at distance x from the wire carring current I.
Side of square =a.
The magnetic field due to current carring wire at a distance x from the wire is B=μ04π.2Ix....(i)
Small amount of magnetic flux associated with the strip
dϕ=B.dA
=μ04π.2Ix.a.dx
(∴dA=area of strip=a.dx from eq (i))
dϕ=μ04π.Iax.dx
Integrate within proper limits, we get
ϕ=μ04π.Iax+a∫x1x.dx⇒ϕ=μ04π.Ia[lnx]x+ax
ϕ=μ04π.Ia[ln(x+a)−In(x)]
ϕ=μ0Ia2πln(x+ax)⇒ϕ=μ0Ia2πln(ax+1)....(ii)
As we know that ϕ=MI......(iii)
where, M is mutual inductance, From equations (ii) and (iii) we get
MI=μ0Ia2πln(ax+1)⇒M=μ0a2πloge(ax+1)
This is mutual inductance between wire and square loop.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Textual Exercise
18 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - DAM SURE LAQ
1 Videos
- ELECTROMAGNETIC WAVEBOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ELECTROMAGNETIC WAVEEXERCISE - ADDITIONAL EXERCISES
19 Videos
Similar Questions
Predict the direction of induced current in the situation described by follow (a)
View SolutionState Gauss's law in electrostatics. Applying Gauss's law derive the expression for electric intensity due to an infinite plane sheet of charge.
View SolutionSuppose that the electric field part of an electromagnetic wave in vacuum is E={(3.1 N/C) cos [(1.8 rad/m)y+{5.4×106 rad/s} t]} i.
What is the direction of propagation ?
View SolutionFind the mutual inductance between the straight wire and the square loop of figure.
View SolutionFind the mutual inductance between the circular coil and the loop shown in figure.
View SolutionThe mutual inductance between the rectangular loop and the long straight wire as shown in figure is M .
View SolutionThe mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
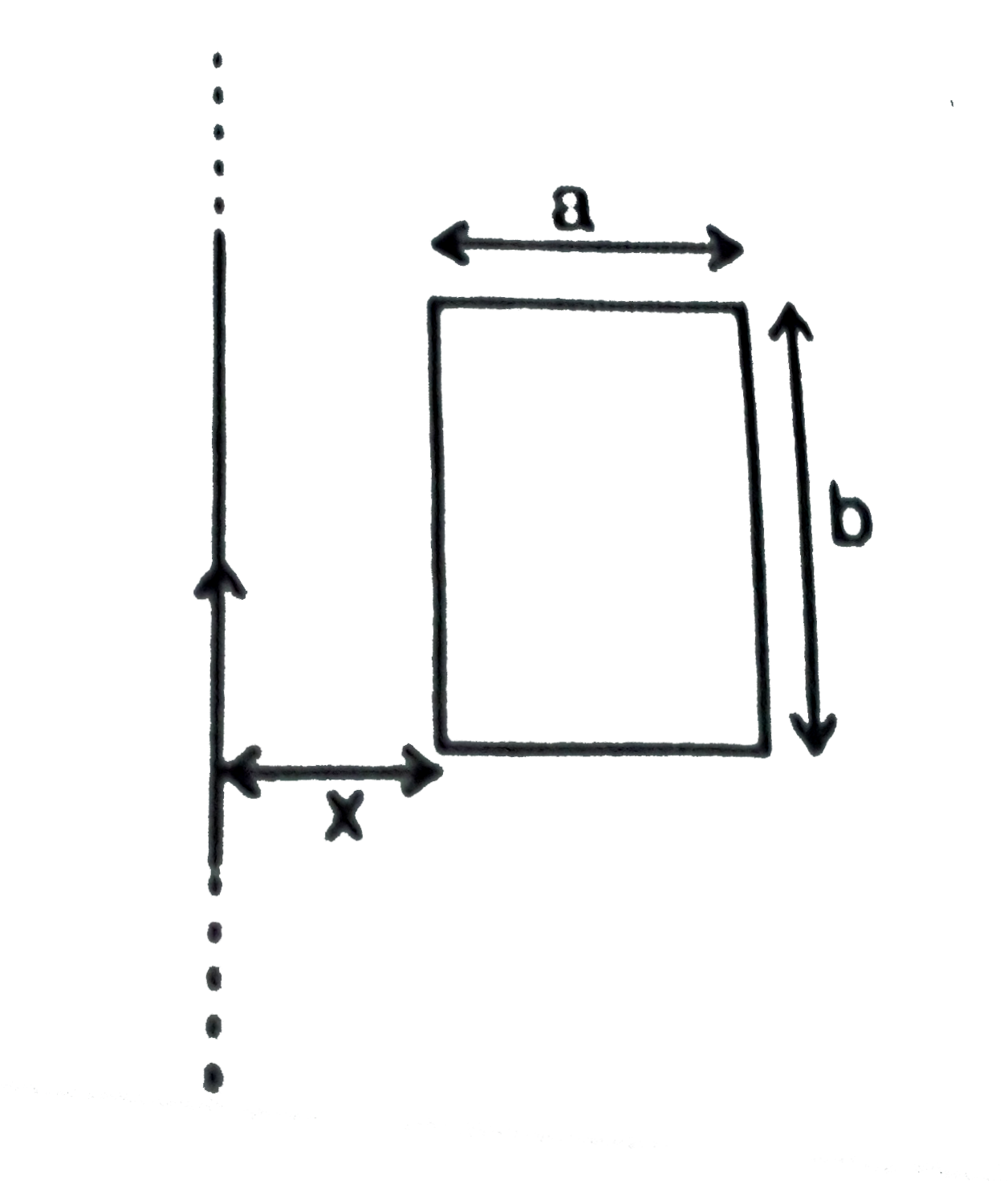
View SolutionObtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in fig.
View Solutionचित्र में प्रदर्शित एक लम्बे सीधे तार तथा a भुजा वाले एक वर्गाकार लूप के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिये |
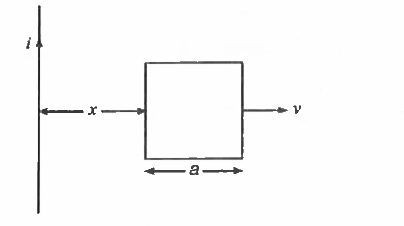
View Solutiona. Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in the figure.
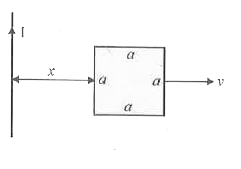
b. Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v=10m/s. Calculate the induced emf in the loop at the instant when x=0.2m. Take a=0.1m and assume that the loop has a large resistance.
View Solution(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in figure. (b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s. Calculate the induced emf in the loop at the instant when x = 0.2 m. Take a = 0.1 m and assume that the loop has a large resistance.
View SolutionAnswer the following:
(a) Define mutual inductance and write its S.I. unit.
(b) A square loop of side a carrying a current I2 is kept at distance x from an infinitely long straight wire carrying a current I1 as shown in the figure. Obtain the expression for the resultant force on the loop.

View SolutionFind the mutual inductance between two rectangular loops, shown in the figure.
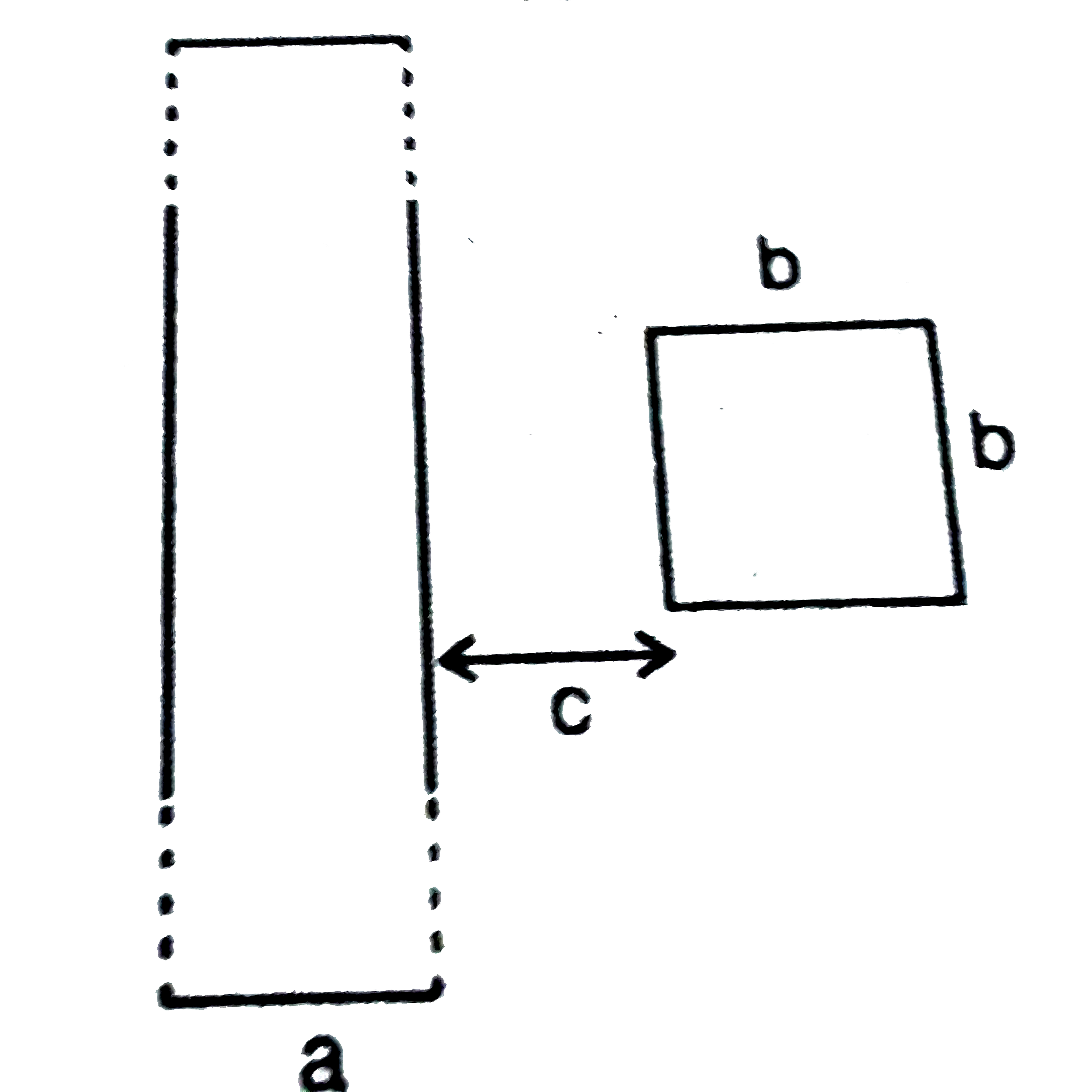
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.

View Solution
