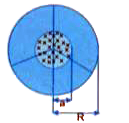
A line charge $λ$ per unit length is lodged uniformly onto the rim of a whell of mass M and radius R. The whell has light non-conducting spokes and is free to rotate without friction about its axis (figure). A uniform magnetic field extends over a circular region withing the rim. It is given by, $B = B_{0} k (r \leq a, a < R)$
What is the angular velocity of the whell after the field is suddenly switched off?

Text Solution

Verified by Experts

Given Linear charge density $λ = \frac{Total charge}{length} = \frac{Q}{2 π R} ... . . (i)$
Radius of rim=M, Magnetic field extends over a circular region
$B = - B_{0} ˆ k (r \leq a, a < R) = O (otherwise)$
Let the angular velocity of the wheel be w, then induced emf $e = \frac{- d ϕ}{d t}$
E exist along circumference of radius a due to change in magnetic flux.
$e \int d I = - \frac{d}{d t} (π a^{2} B) \Rightarrow E \times 2 π a = - π a^{2} \frac{d B}{d t} \Rightarrow E = \frac{a}{2} . \frac{d B}{d t}$
Force on charge $(F) = Q E = (2 π a \times λ) (- \frac{a}{2} . \frac{d B}{d t}) = - π a^{2} λ \frac{d B}{d t}$
But force (F) $= \frac{d P}{d t} = \frac{d (M V)}{d t} = M . \frac{d V}{d t} \Rightarrow M . \frac{d V}{D T} = - π a^{2} λ \frac{d B}{d t} (∴ V = R W)$
MR(dW) $= - π a^{2} λ \frac{d B}{d t} \Rightarrow d W = - \frac{π a^{2} λ}{M R}, d B, Integrating both sides ω = - \frac{π a^{2} λ B}{M R}$
As direction of angular velocity is along axis $ω = \frac{λ a^{2} π}{M R} B υ$

Updated on:21/07/2023