A source contains two phosphorous radio nuclides $._{15}^{32} P (T_{1 / 2} = 14.3 d)$ and $._{15}^{33} P (T_{1 / 2} = 25.3 d)$ . Initially, 10% of the decays come from $._{15}^{33} P$ . How long one must wait until 90% do so ?

Text Solution

Verified by Experts

Suppose initially the source has 90% $._{15} P t^{32}$ and 10% $._{15} P_{1}^{32}$ , say 9x gram of $P_{2}$ and x gram of $P_{1}$ . After t days, suppose the source has 90% $._{15} P_{2}^{33}$ and $10 % ._{15} P_{t}^{32}$ i.e., y gram of $P_{2}$ and 9y gram of $P_{1}$
we have to calculate :
from $\frac{N}{N_{0}} = {(\frac{1}{2})}^{n} = {(\frac{1}{2})}^{t / T} = 2^{- i / T}$
$N = N_{0} 2^{- t / T}$
$y = 9 x 2^{- t / 14.3}$ for $P_{2}$ and $9 y = x 2^{- t / 25.3}$ for $P_{1}$ Dividing we get
$\frac{1}{9} = 9 \times 2 (t / 25.3 - t / 14.3)$
or $\frac{1}{81} = 2^{- 11 t / 25.3} \times 14.3$
log 1 - log $81 = \frac{- 11 t}{25.3 \times 14.3}$ log 2
$0 - 1 - 9085 = \frac{- 11 t}{25.3 \times 14.3} \times 0.3010$ .
$t = \frac{25.3 \times 14.3 \times 1.9085}{11 \times 0.3010} = 208.5$ days.

Updated on:21/07/2023

Class 12 PHYSICS NUCLEI

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
For an ideal gas, an illustratio of three different paths $A (B + C)$ and $(D + E)$ from an initial state $P_{1}, V_{1}, T_{1}$ to a final state $P_{2}, V_{2}, T_{1}$ is shown in the given figure.

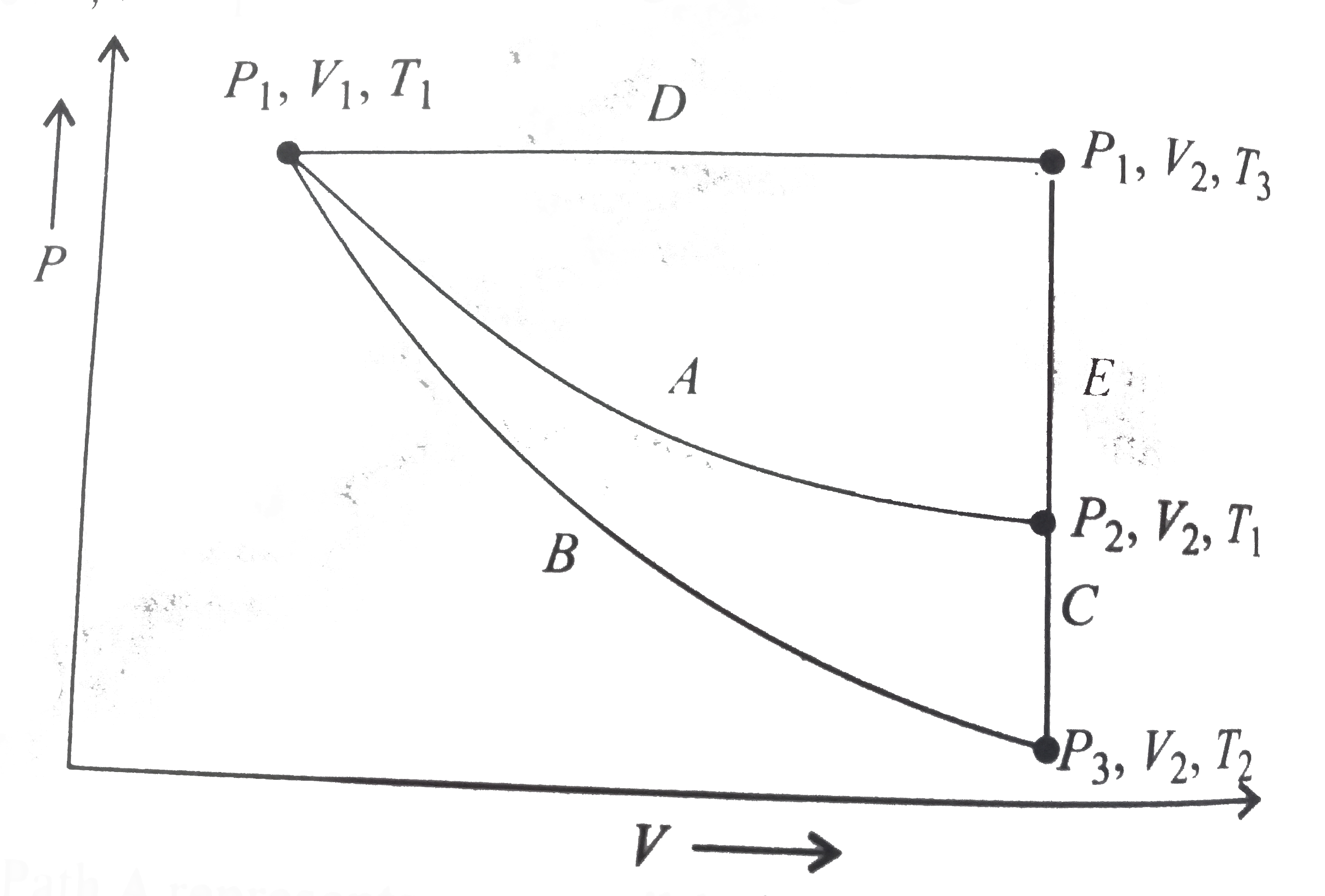
Path $A$ represents a reversible isothermal expansion form $P_{1}, V_{1}$ to $P_{2}, V_{2}$ , Path $(B + C)$ represents a reversible adiabatic expansion $(B)$ from $P_{1}, V_{1}, T_{1} \to P_{3}, V_{2}, T_{2}$ followed by reversible heating the gas at constant volume $(C)$ from $P_{3}, V_{2}, T_{2}$ to $P_{2}, V_{2}, T_{1}$ . Path $(D + E)$ represents a reversible expansion at constant pressure $P_{1} (D)$ from $P_{1}, V_{1}, T_{1}$ to $P_{1}, V_{2}, T_{3}$ followed by a reversible cooling at constant volume $V_{2} (E)$ from $P_{1}, V_{2}, T_{3} \to P_{2}, V_{2}, T_{1}$ .
What is $q_{r e v}$ , for path $(D + E)$ ?
A $P (V_{2} - V_{1})$
B $\int_{T_{3}}^{T_{1}} \frac{C_{V} (T)}{T} d T$
C $n R I n \frac{V_{2}}{V_{1}}$
D $\int_{T_{1}}^{T_{3}} C_{V} (T) d T$
Question 2 - Select One
For an ideal gas, an illustratio of three different paths $A (B + C)$ and $(D + E)$ from an initial state $P_{1}, V_{1}, T_{1}$ to a final state $P_{2}, V_{2}, T_{1}$ is shown in the given figure.

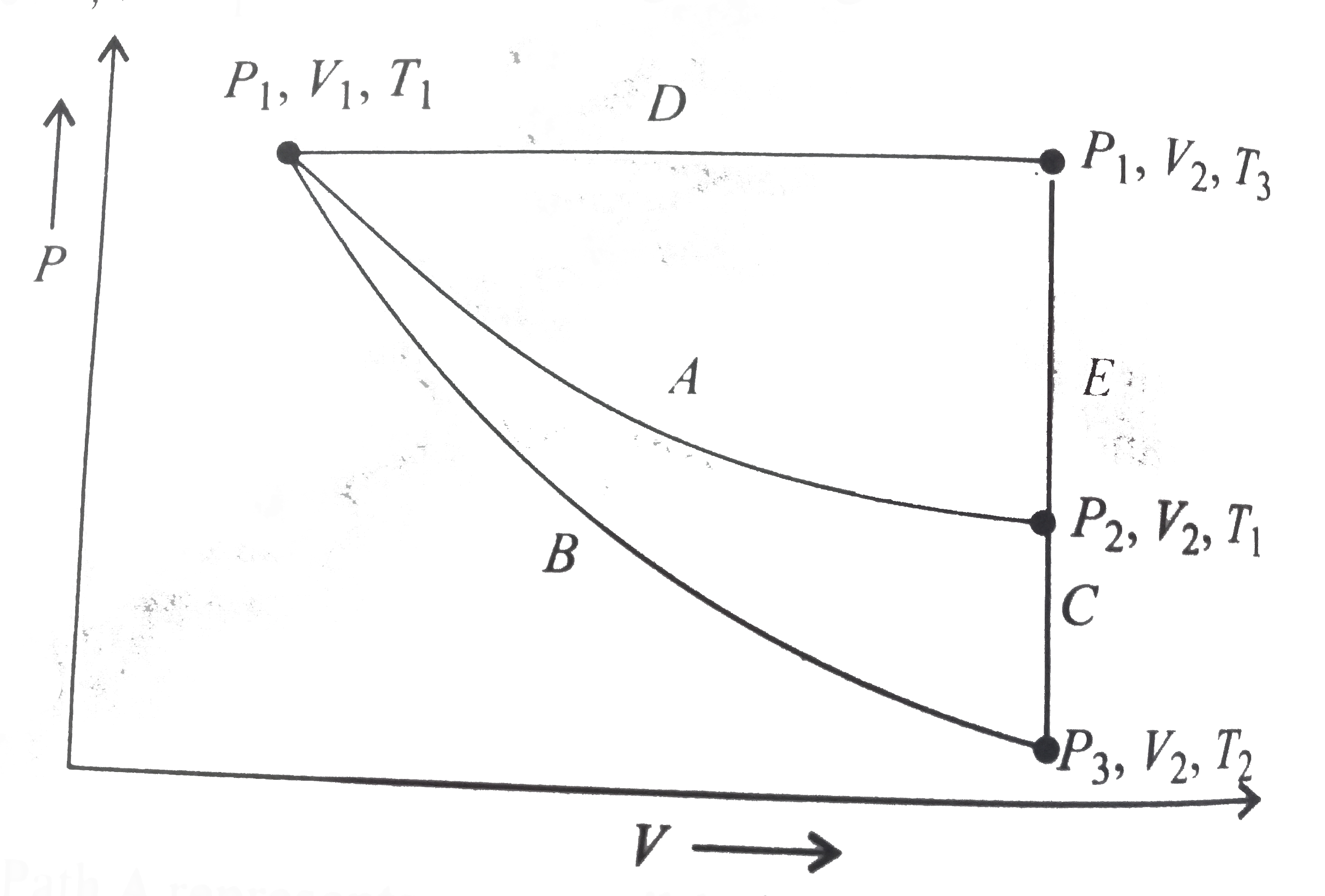
Path $A$ represents a reversible isothermal expansion form $P_{1}, V_{1}$ to $P_{2}, V_{2}$ , Path $(B + C)$ represents a reversible adiabatic expansion $(B)$ from $P_{1}, V_{1}, T_{1} \to P_{3}, V_{2}, T_{2}$ followed by reversible heating the gas at constant volume $(C)$ from $P_{3}, V_{2}, T_{2}$ to $P_{2}, V_{2}, T_{1}$ . Path $(D + E)$ represents a reversible expansion at constant pressure $P_{1} (D)$ from $P_{1}, V_{1}, T_{1}$ to $P_{1}, V_{2}, T_{3}$ followed by a reversible cooling at constant volume $V_{2} (E)$ from $P_{1}, V_{2}, T_{3} \to P_{2}, V_{2}, T_{1}$ .
What is $Δ S$ for path $(D + E)$ ?
A $- P (V_{2} - V_{1})$
B $- n R I n \frac{V_{2}}{V_{1}}$
C $+ P (V_{2} - V_{1})$
D $n R I n \frac{V_{2}}{V_{1}}$

VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-NUCLEI-ADDITIONAL EXERCISES

Home
Ask Doubt
Profile

A source contains two phosphorous radio nuclides .3215P(T1/2=14.3d) and .3315P(T1/2=25.3d). Initially, 10% of the decays come from .3315P. How long one must wait until 90% do so ?

Topper's Solved these Questions

Similar Questions

Knowledge Check

VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-NUCLEI-ADDITIONAL EXERCISES

A source contains two phosphorous radio nuclides $._{15}^{32} P (T_{1 / 2} = 14.3 d)$ and $._{15}^{33} P (T_{1 / 2} = 25.3 d)$ . Initially, 10% of the decays come from $._{15}^{33} P$ . How long one must wait until 90% do so ?