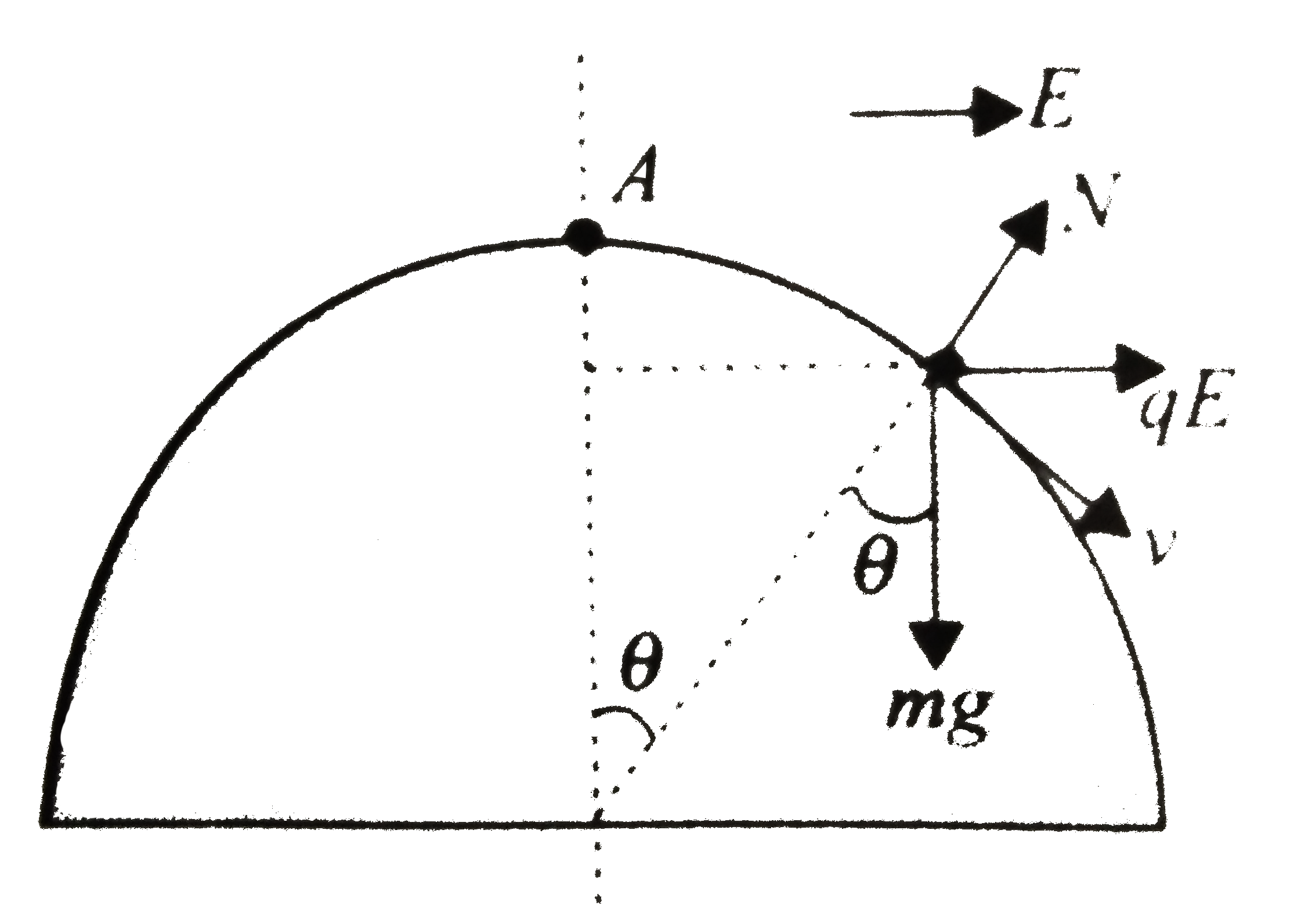
In a horizontal unifrom electirc field, a small charged disk is gently released on the top of a fixed sperical dome. The disk slides down the some without friction and breaks away from the surface of the dome at the angular position θ=sin−1(3/5) from verical. Determine the ration of the force of gravity acting on the disk to force of its interaction with the field .

Motoin fron A to B
mgR(1−cosθ)+qERsinθ=mv22
Given sinθ=35
∴cosθ=45
∴mgR(15)+qER(35)=mv22
or (mg+3qE)=52mv2R …(i)
Also the equation of circular motion is
mgcosθ−N−qEsinθ=mv2R
When the paricle loses contact , N=0,sinθ=35, and cosθ=45.Therefore ,
mg(45)−qE(35)=mv2R
or, 4mg−3qE=5mv2R ...(ii)
Form Eqs, (i) and (ii), mg+3qE4mg−3qE=12
or, 2mg+6qE=4mg−3qE
or , 2mg=9qE or mgqE=92.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
A small coin is placed on a flat, horizontal turbtable. The turnable is observed to make three revolutions is 3.14 s. (a) What is the speed of the coin when it rides without slipping at a distance of 5.0 cm from the center of the turntable? (b) What is the acceleration (magnitude and direction) of the coin? (c) What are the magnitude and direction of the frictional force acting on the coi if the coin has a mass of 2.0 g? (d) What is the coefficient of static friction between the coin and the turntable if the coin is observed to slide off the turntable when it is more than 10 cm from the center of the turntable?
View SolutionTwo thin rings of slightly different radii are joined together to make a wheel (see figure) of radius R. There is a very small smooth gap between the two ring. The wheel has a mass M and its centre of mass is at its geometrical centre. The wheel stands on a smooth surface and a small particle of mass m lies at the top (A) in the gap between the rings. The system is released and the particle begins to slide down along the gap. Assume that the ring does not lose contact with the surface.

(a) As the particle slides down from top point A to the bottom point B, in which direction does the centre of the wheel move?
(b) Find the speed of centre of the wheel when the particle just reaches the bottom point B. How much force the particle is exerting on the wheel at this instant?
(c) Find the speed of the centre of the wheel at the moment the position vector of the particle with respect to the centre of the wheel makes an angle q with the vertical. Do this calculation assuming that the particle is in contact with the inner ring at desired value of θ
View Solution
Knowledge Check
A samll object of mass 10.0 g is at rest 30.0 cm from a horizontal disk's centre. The disk starts to rotate from rest about its centre with a constant angular acceleration of 4.50 rad/s2. What is the magnitude of the net force acting on the object after a time of t=13 s if the object remains at rest with respect to the disk ?
A0NB1.5×10−2NC7.4×10−3ND1.8×10−2NA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
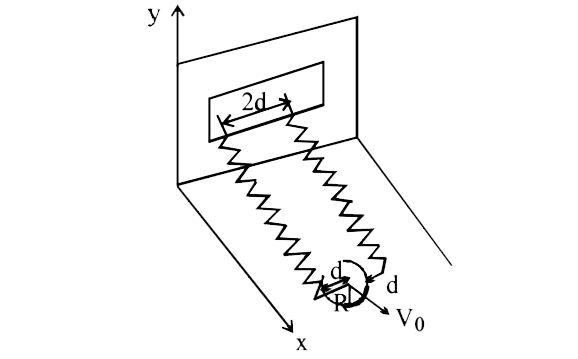
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.A=−kxB−2kxC−2kx/sD−4kx/3In the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B. Find the maximum force exerted by track on the sphere during its motion.
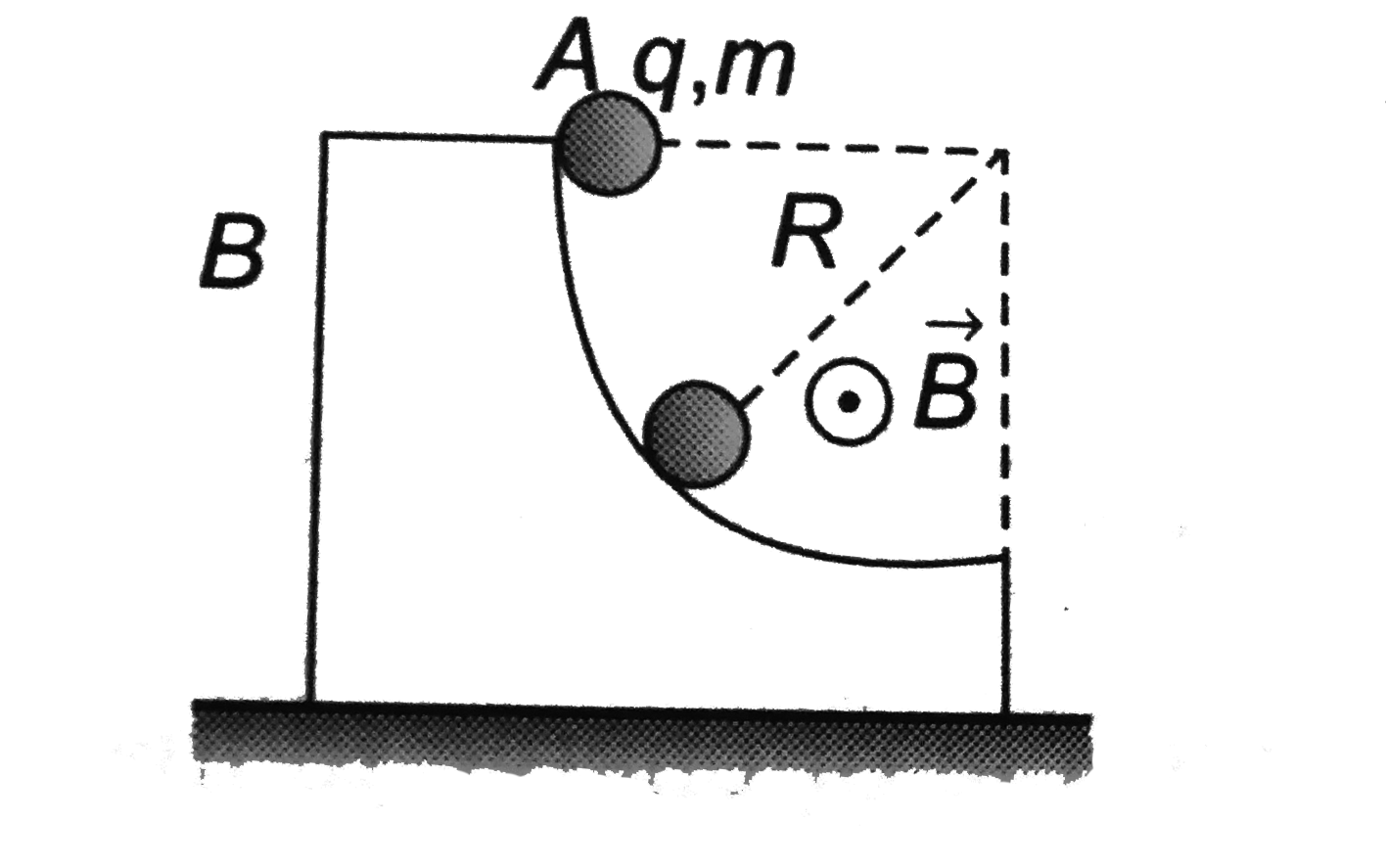 ANmax=2mg+qB√2gRBNmax=3mg+qB√2gRCNmax=3mg+2qB√2gRDNmax=3mg+qB√gR
ANmax=2mg+qB√2gRBNmax=3mg+qB√2gRCNmax=3mg+2qB√2gRDNmax=3mg+qB√gR
A small circular coil with a mass of m consists of N turns of fine wire and carries a current of I. The coil is located in a uniform magnetic field of B with the coil axis orginally parallel to the field direction.

a. What is the period of small angle oscilations of the coil axis around its equilibrium position, assuming no friction and no mechanical force?
b. If the coil is rotated through an angle of θ from its equilibrium position and then released, what will be its angular speed when it passes through equilibrium position?
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA point mass m=1kg is attached to a point P on the circumference of a uniform ring of mass M=3kg and radius R=2.0m. The ring is placed on a horizontal surface and is released from rest with line OP in horizontal position (O is centre of the ring). Friction is large enough to prevent sliding. Calculate the following quantities immediately after the ring is released-
(a) angular acceleration (α) of the ring,
(b) normal reaction of the horizontal surface on the ring and
(c) the friction force applied by the surface on the ring.
[Take g=10m/s2 ]

View SolutionIn a neutral conducting hollow sphere of inner and outer radii 5 cm and 10 cm respectively, a point charge Q = 1C is placed at point A, that is 3 cm from the centre C of the hollow sphere. An external uniform electric field of magnitude 20 N/C is also applied. Net electric force on this charge is 15 N, away from the centre of the sphere as shown. Then find :
(a) Force due to external electric field on the outer surface of the shell
(b)Net force on shell.
(c) Net force on point charge due to shell.

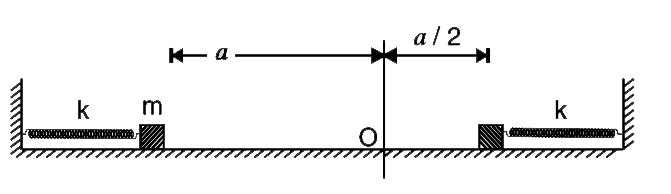
View Solution(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.

View Solution
