A block of mass ma is suspended vertically with a spring of spring constant k. The block is made to oscillate in a gravitation field. Its time period is found to be T. Now the space between the plates is made gravity free, and an electric field E is produced in the downward direction. Now the block is given a charge q. the new time period of oscillation is

T
T+2π√qEmd
2π√qEmd
none of the above
The correct Answer is:A
Time period is independent of a constant force acting on the block of spring-block system. Its time period will remain same as
T=2π√mk.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension25videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective32videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK19videos
COMMUNICATION SYSTEM
- BOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK40videos
Current Electricity
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
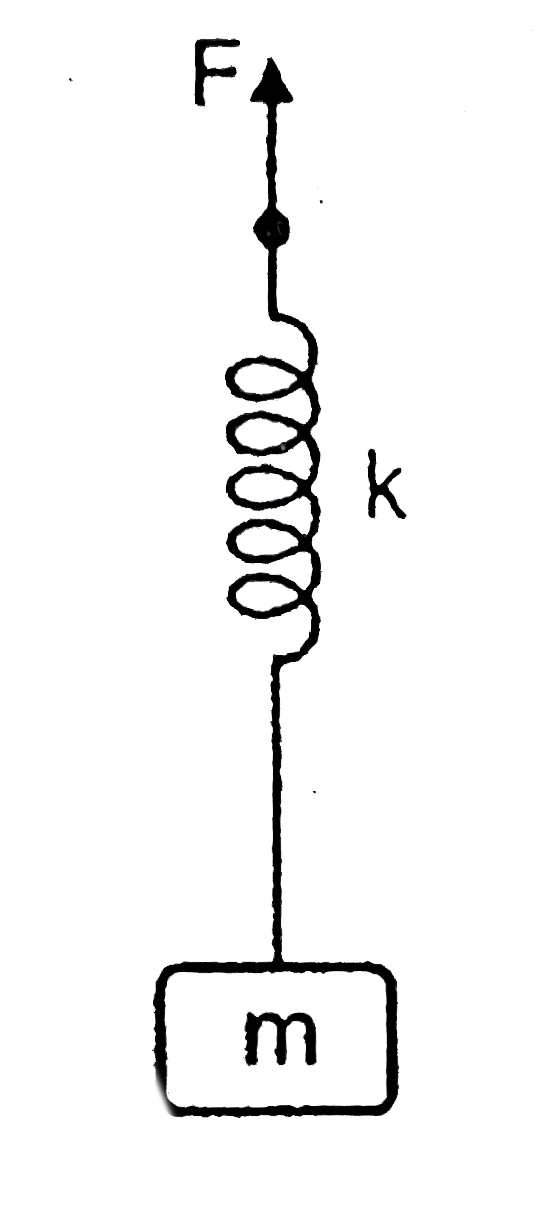 Amαk−gt−αt22Bmαk−gt−αt2Cmαk−gt+αt22Dmαk+gt+αt22
Amαk−gt−αt22Bmαk−gt−αt2Cmαk−gt+αt22Dmαk+gt+αt22 - Question 2 - Select One
A block of mass m is suspended by different springs of force constant shown in figure Let time period of oscillation in these four positions be T1,T2,T3 and T4. Then :
 AT1=T2=T4BT1=T2 and T3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2 and T3=T4CT1=T2=T3DT1=T3 and T2=T4 - Question 3 - Select One
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionTwo blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.
 View Solution
View SolutionA block of mass m is suspended by different springs of force constant shown in figure. Let time period of oscillation in these four positions be T1,T2,T3andT4 Then -
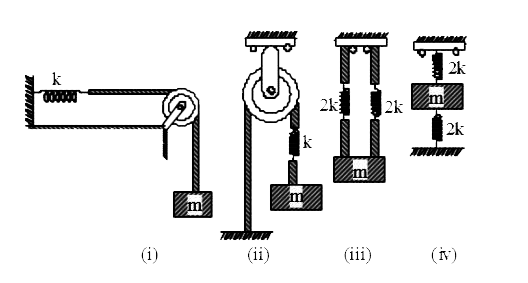 View Solution
View SolutionTime period of a block when suspended from the upper plate of a parallel plate capacitor by a spring of stiffness k is T, when block is uncharged. If a charge g is given to the block then new time period of oscillation will be
 View Solution
View Solution

