A block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
To find the time period of oscillations for the block connected to three springs, we can follow these steps:
Step 1: Understand the System
The block of mass m is connected to three springs. When the block is displaced downward slightly and released, it will start oscillating. We need to analyze the forces acting on the block due to the springs.
Step 2: Define Displacements
Let:
- y be the downward displacement of the block.
- y′ be the compression of the two springs on the sides.
Due to the geometry of the setup, we can relate y′ to y using trigonometric relationships.
Step 3: Relate y′ and y
From the geometry of the springs and the angle θ:
y′=ycosθ
This relationship indicates how the compression in the springs is related to the vertical displacement of the block.
Step 4: Calculate the Forces
The forces acting on the block due to the springs can be calculated. Since the springs are in parallel, the total force F exerted by the springs can be expressed as:
F=−k1y′−k2y
Substituting y′ from the previous step:
F=−k1(ycosθ)−k2y
This simplifies to:
F=−y(k1cosθ+k2)
Step 5: Apply Newton's Second Law
According to Newton's second law, the acceleration a of the block is given by:
F=ma
Substituting our expression for F:
ma=−y(k1cosθ+k2)
This can be rewritten as:
a=−y(k1cosθ+k2)m
Step 6: Relate to Simple Harmonic Motion
For simple harmonic motion, we have:
a=−ω2y
By comparing the two equations, we can identify:
ω2=k1cosθ+k2m
Step 7: Calculate the Time Period
The time period T of oscillation is related to the angular frequency ω by:
T=2πω
Substituting for ω:
T=2π√mk1cosθ+k2
Conclusion
Thus, the time period of oscillations for the block connected to three springs is given by:
T=2π√mk1cosθ+k2
The block of mass m is connected to three springs. When the block is displaced downward slightly and released, it will start oscillating. We need to analyze the forces acting on the block due to the springs.
Let:
- y be the downward displacement of the block.
- y′ be the compression of the two springs on the sides.
From the geometry of the springs and the angle θ:
y′=ycosθ
This relationship indicates how the compression in the springs is related to the vertical displacement of the block.
The forces acting on the block due to the springs can be calculated. Since the springs are in parallel, the total force F exerted by the springs can be expressed as:
F=−k1y′−k2y
Substituting y′ from the previous step:
F=−k1(ycosθ)−k2y
This simplifies to:
F=−y(k1cosθ+k2)
According to Newton's second law, the acceleration a of the block is given by:
F=ma
Substituting our expression for F:
ma=−y(k1cosθ+k2)
This can be rewritten as:
a=−y(k1cosθ+k2)m
For simple harmonic motion, we have:
a=−ω2y
By comparing the two equations, we can identify:
ω2=k1cosθ+k2m
The time period T of oscillation is related to the angular frequency ω by:
T=2πω
Substituting for ω:
T=2π√mk1cosθ+k2
Thus, the time period of oscillations for the block connected to three springs is given by:
T=2π√mk1cosθ+k2
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q
78 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -I (C.W)
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A block of mass m is connected to three springs as shown in the figure. The block is displaced down slightly and left free, it starts oscillating. Find the time period of oscillations (neglecting gravity). (m−π2(~kg):π2m10,θ−60∘,k1=4N / m , ki=23Nm)
'(##CEN_KSR_PHY_JEE_C16_E01_025_Q10##)'
View SolutionA small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
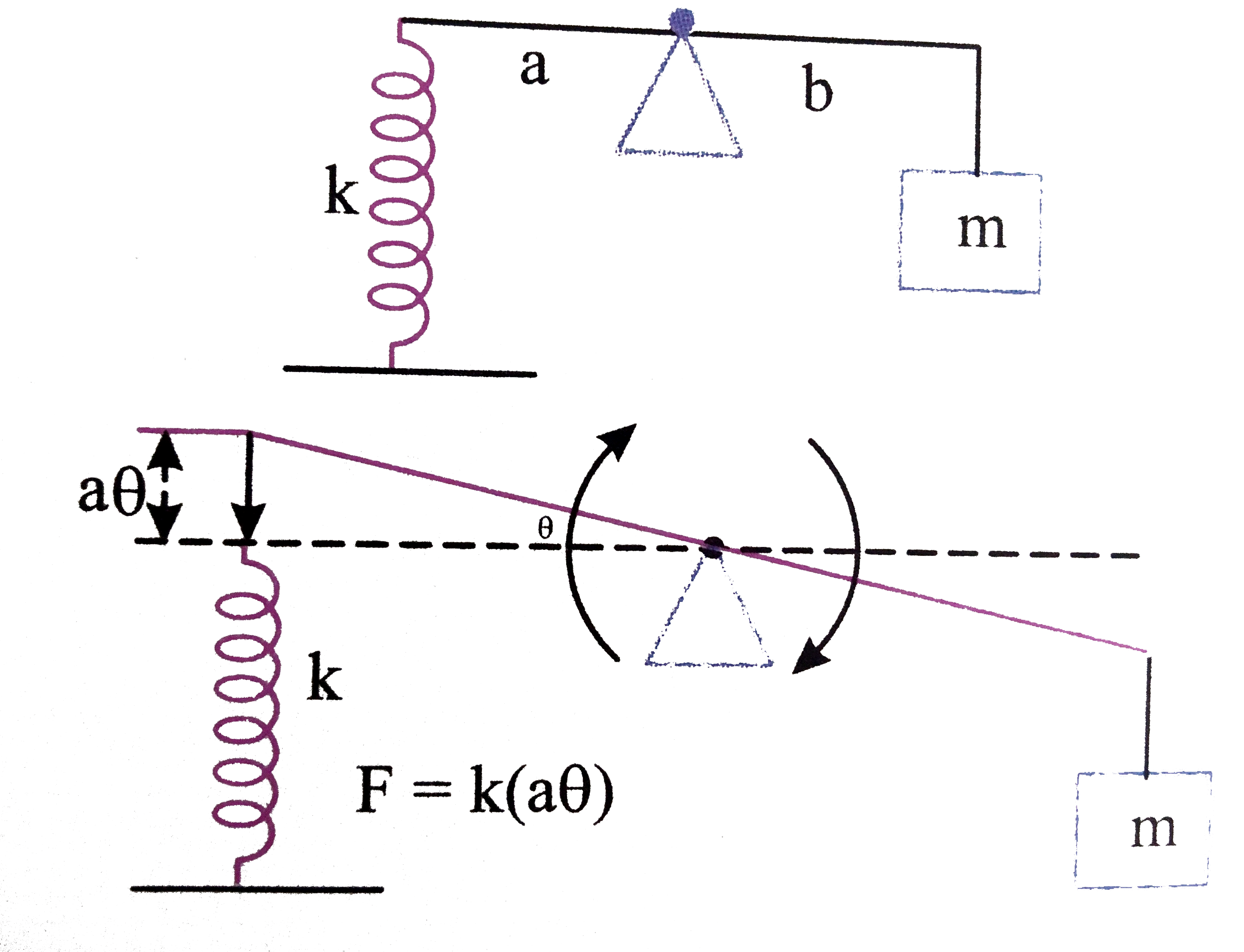
View Solution
Knowledge Check
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmA small block is connected to a massless rod, which in turns attached to a spring of force constnat (K=2N/m) as shown in the fig. The block is displaced down slightly and left free. Find its time period.
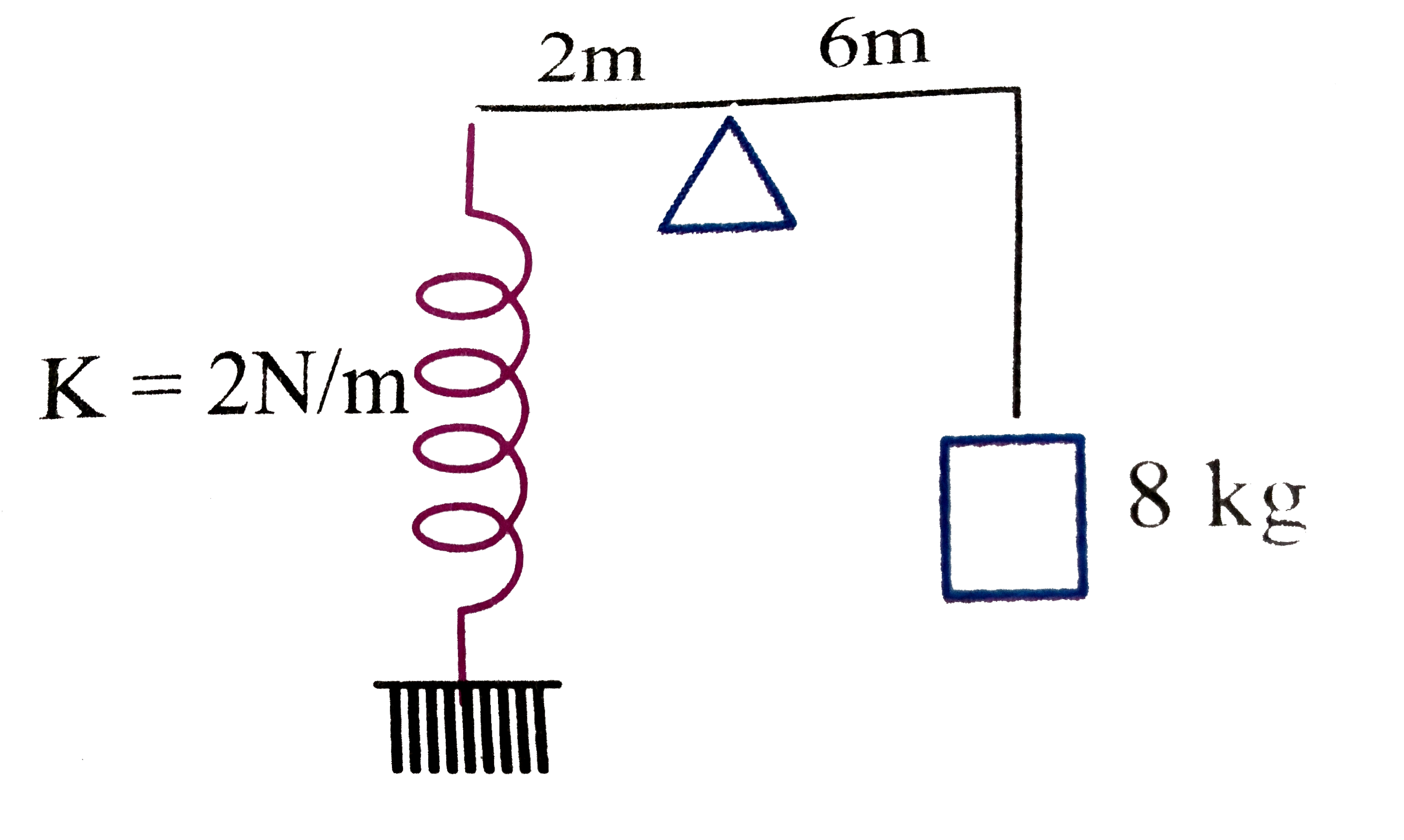 AπsecB2πsecC6πsecD12πsec
AπsecB2πsecC6πsecD12πsecA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be
 A2π√AlmYB2π√AYmlC2π√mlYAD2π√mYal
A2π√AlmYB2π√AYmlC2π√mlYAD2π√mYal
A plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these osillations.

View SolutionA block of mass 'm' is connected to the lower end of a massless vertically suspended spring. The ball is displaced slightly downward and released, it oscillates up and down. Match the coloum I and column II

View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View SolutionIn the device shown in Fig, the block m is displaced down slightly and released. It starts oscillating. Pulleys are smooth and massless string and springs are also massless. Find time period of oscillations.

View Solution
A uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring is
View Solution
