If an isolated infinite plate contains a charge on one of its surfaces and a charge on its other surface, then prove that electric field intensity at a point in front of the plate will be , where
Let us take a point P right of the plate.
The electric field at P is the vector sum of the
field due to both the surfaces. Hence,
.
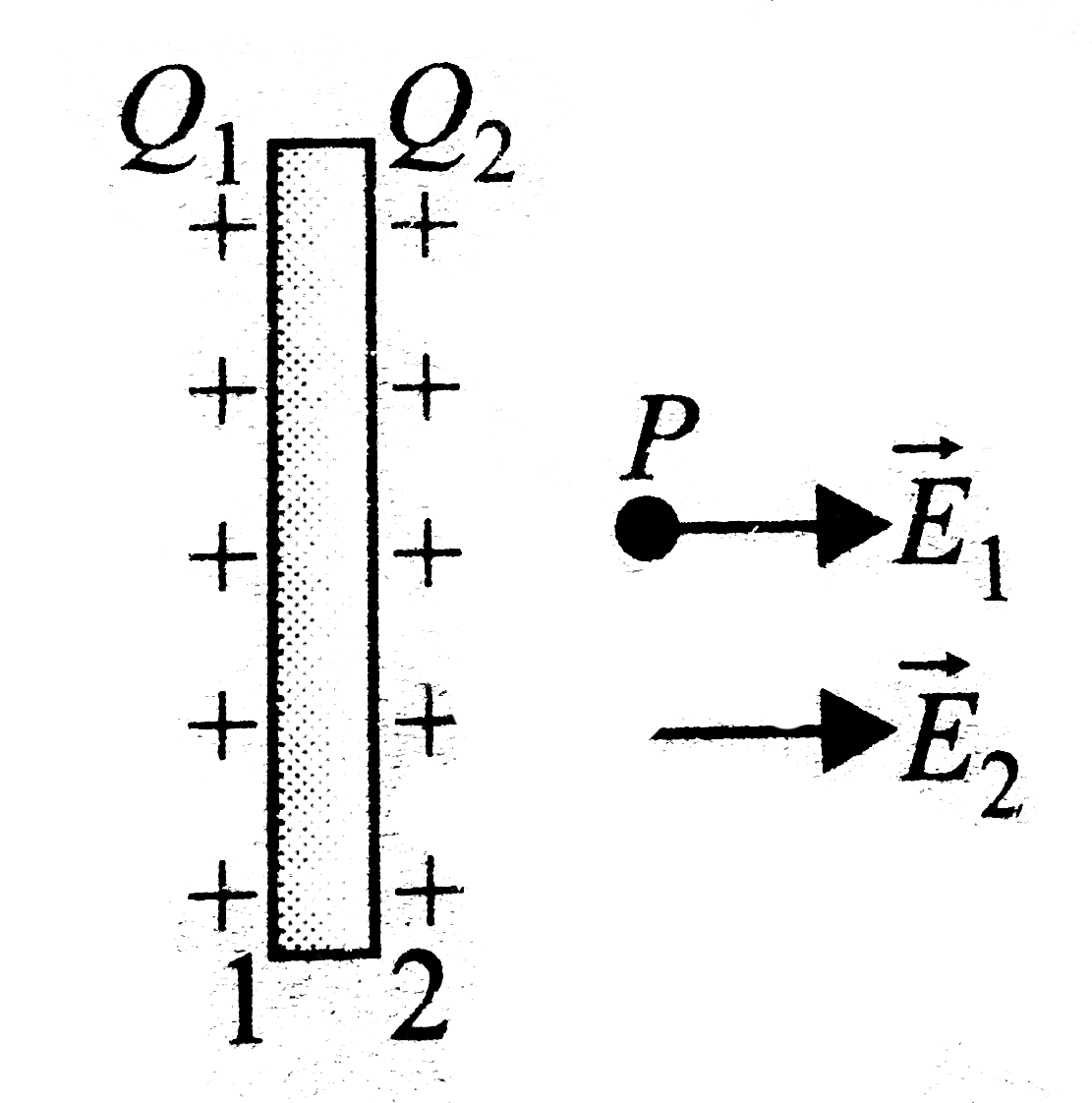 .
.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
If an isollated infinite sheet contains charge Q1 on its one surface and charge Q2 on its other surface, then prove that electric field intensity at a point in front of sheet will be Q2Aε0, where Q=Q1+Q2
View SolutionCharge 2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be somewhere

View Solution
Knowledge Check
If q is the charge per unit area on the surface of a conductor, then the electric field intensity at a point on the surface is
A(qε0) normal to surfaceB(q2ε0) normal to surfaceC(qε0) tangential to surfaceD(q2ε0) tangential to surfaceEach of two large conducting parallel plates has one sided surface area A. If one of the plates is given a charge Q whereas the other is neutral, then the electric field at a point in between the plates is given by
AQAε0BQ2Aε0CQ4Aε0DZeroCharges +2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be
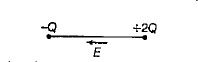 ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2Q
ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2Q
Suppose a charge +Q1 is given to the positive plates and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
View SolutionA charge Q is enclosed by a Gaussian surface. If surface area is doubled and charge Q is tripled then the outward electric flux will
View SolutionThe ratio of charge on left surface of plate A to the charge on the right surface of plate B is +Q +3Q -20 (A) (B) (C)
View SolutionIn a parallel plate capacitor with plate area A and charge Q, the force on one plate because of the charge on the other is equal to
View SolutionIn an isolated parallel plate capacitor of capacitance C the four surfaces have charges Q1,Q2,Q3 and Q4 as shown in the figure. The potential difference between the plates is :
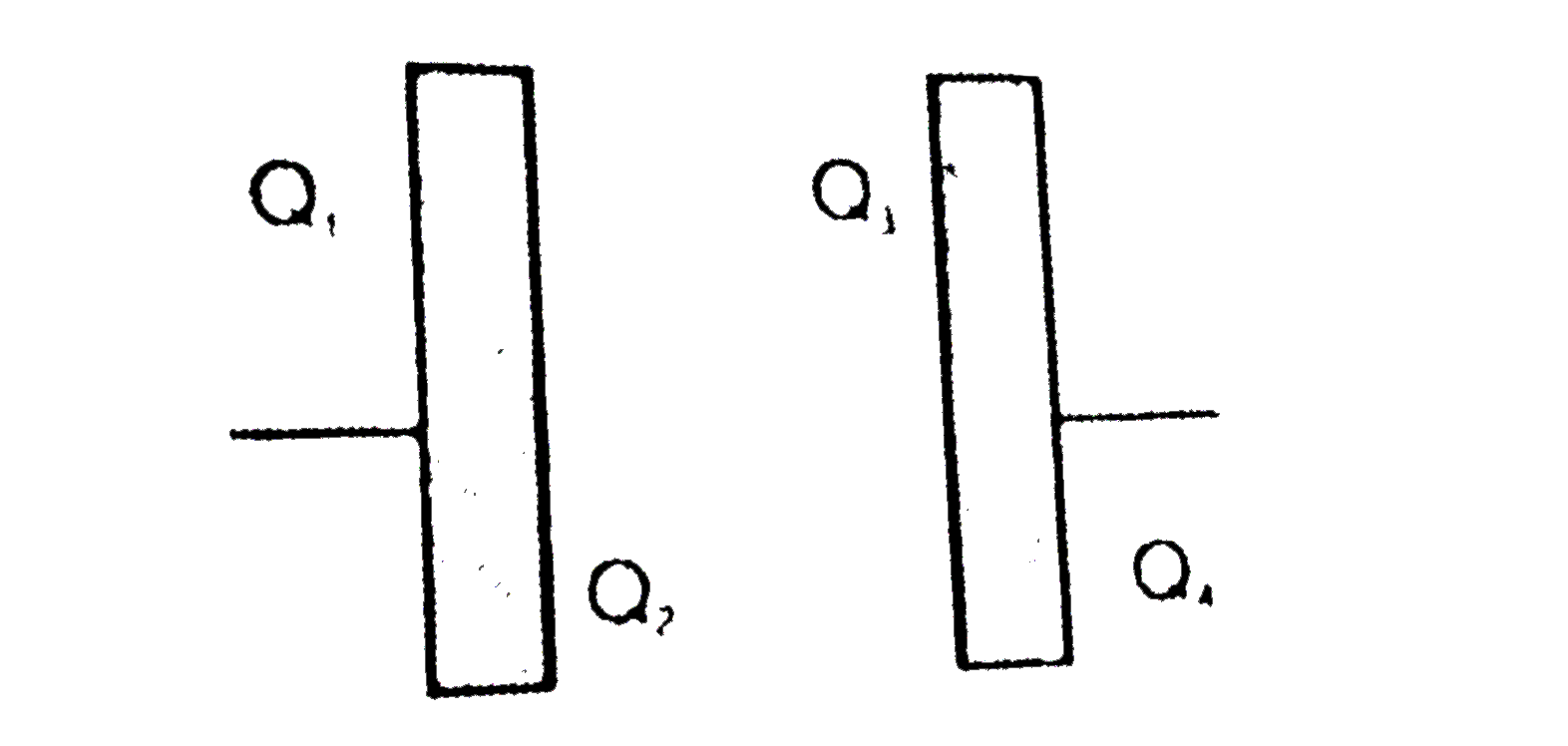
View Solution
