A cube of side 10 cm encloses a charge of 0.1μC at its center. Calculate the number of lines of force through each face of the cube.
1.113×1011
1.13×104
1.13×109
1883
The correct Answer is:D
To solve the problem of calculating the number of lines of force through each face of a cube enclosing a charge, we can follow these steps:
Step 1: Understand the Concept of Electric Flux
Electric flux (Φ) through a closed surface is given by Gauss's Law, which states:
Φ=Qε0
where Q is the total charge enclosed and ε0 is the permittivity of free space.
Step 2: Identify the Given Values
- The charge Q=0.1μC=0.1×10−6C=1×10−7C
- The permittivity of free space ε0=8.854×10−12C2/(N⋅m2)
Step 3: Calculate the Total Electric Flux through the Cube
Using Gauss's Law:
Φ=Qε0=1×10−78.854×10−12
Calculating this gives:
Φ≈1.13×104N⋅m2/C
Step 4: Calculate the Electric Flux through One Face of the Cube
Since the cube has 6 faces, the electric flux through each face is:
Φface=Φ6=1.13×1046≈1.88×103N⋅m2/C
Step 5: Calculate the Number of Lines of Force
The number of lines of force is proportional to the electric flux. Therefore, the number of lines of force through each face of the cube is approximately:
Number of lines of force through each face≈1883
Final Answer
The number of lines of force through each face of the cube is approximately 1883.
---
Electric flux (Φ) through a closed surface is given by Gauss's Law, which states:
Φ=Qε0
where Q is the total charge enclosed and ε0 is the permittivity of free space.
- The charge Q=0.1μC=0.1×10−6C=1×10−7C
- The permittivity of free space ε0=8.854×10−12C2/(N⋅m2)
Using Gauss's Law:
Φ=Qε0=1×10−78.854×10−12
Φ≈1.13×104N⋅m2/C
Since the cube has 6 faces, the electric flux through each face is:
Φface=Φ6=1.13×1046≈1.88×103N⋅m2/C
The number of lines of force is proportional to the electric flux. Therefore, the number of lines of force through each face of the cube is approximately:
Number of lines of force through each face≈1883
The number of lines of force through each face of the cube is approximately 1883.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
Knowledge Check
- Question 1 - Select One
A cube of side L encloses a charge Q at its centre , electric flux through the cube is
AQ∈0BQ6L2∈0CQL2∈0Dzero - Question 2 - Select One
A metal cube of side 10cm is subjected to a shearing stress of 106N/m2. Calculate the modulus of rigidity if the of the cube is displaced by 0.05cm with respect to its bottom.
A1×108N/m2B2×108N/m2C3×108N/m2D4×108N/m2 - Question 3 - Select One
A charge Q=1.8μC is placed at the centre of a cube of adge 55 cm. The electric flux through one of the faces of the cube is
AQ/ε0BQ/2ε0CQ/4ε0DQ/6ε0
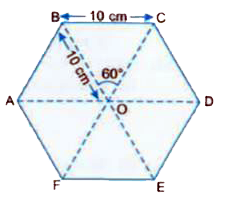
A regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
 View Solution
View SolutionTwo charges +0.4μC and−0.2μC are placed on adjacent vertices of a square of side 10 cm. Another charge of 1.2μC is placed at the centre af the square Calculate the force and its direction in the charge kept in the centre .
View SolutionIf a point charge q is placed at the centre of a cube.
What is the flux linked (a) with the cube? (b) with each face of the cube?View SolutionA charge of q μC is placed at the centre of a cube of side 0.1 m. the electric flux diverging from each face of the cube will be
View SolutionEight charges, 1muC, -7muC , -4muC, 10muC, 2muC, -5muC, -3muC, and 6muC, are situated at the eight cornersof a cube of side 20 cm. A spherical surface of radius 80 cm encloses this cube. The center of the sphere coincides with the center of the cube. Then, the total outgoing flux from the spherical surface (in units of Vm) is
View Solution

