The electric field →E1 at one face of a parallelopiped is uniform over the entire face and is directed out of the face. At the opposite face, the electric field →E2 is also uniform over the entire face and is directed into that face (as shown in figure). The two faces in question are inclined at 30∘ from the horizontal, →E1and→E2(both horizontal) have magnitudes of 2.50×104NC−1 and 7.00×104NC−1. respectively. Assuming that no other electric field lines cross the surfaces of the parallelopiped, the net charge contained with in is

A
−67.5ε0C
B
37.5ε0C
C
105ε0C
D
−105ε0C
Video Solution
Text Solution
The correct Answer is:A
a. To find the charge enclosed,
we need the flux through the
parallelepiped:
Φ1=AE1cos60∘
=(0.0500m)(0.0600m)(2.50×104NC−1)cos60∘
=37.5Nm2C−1
Φ2=AE2cos120∘
=(0.0500m)(0.0600m)(7.00×104NC−1)cos120∘
=−105Nm2C−1
So the flux is
Φ=Φ1+Φ2=(37.5−105)Nm2C−1=−67.5Nm2C−1
q=Φε0=(−67.5Nm2C−1)ε0=−5.97×10−10C
There must be a net charge (negative) in the parallelepiped since
there is a net flux flowing into the surface. Also, there must be an
external field, otherwise all lines would point towards the slab.
|
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Comprehension
Explore 36 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
Knowledge Check
Which number is on the face opposite to face having number 1?
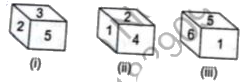 A2B3C4D5
A2B3C4D5
How many dots will be there on the face opposite to the face with 2 dots?

View SolutionWhich number is on the face opposite to face having number 3?

View SolutionA solid that has two opposite identical faces and other faces as parallelograms is a
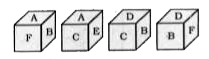
View SolutionFrom the positions of a cube shown below, which letter will be on the face opposite to face with A?
View SolutionFind the digit at the face opposite to the face having digit 4 in the given dice.

View SolutionA metal slab is placed in a uniform electric field →E. What will be the net electric field intensity inside it?
View SolutionWhich number appear in the face opposite to the face with number 4?
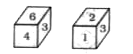
View Solution


