A particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
To solve the problem, we need to analyze the forces acting on the charged particle and apply the principles of circular motion. Here is a step-by-step solution:
Step 1: Identify the Forces
The forces acting on the particle are:
- Weight (mg) acting downward.
- Electric force (F_e = qE) acting horizontally due to the electric field.
- Tension (T) in the thread, which has components in both vertical and horizontal directions.
Step 2: Set Up the Equations
When the particle is in equilibrium (at rest), the following equations hold true:
1. Vertical Forces: The vertical component of the tension balances the weight of the particle.
Tcosθ=mg(1)
2. Horizontal Forces: The horizontal component of the tension balances the electric force.
Tsinθ=qE(2)
Step 3: Divide the Equations
Dividing equation (2) by equation (1) gives:
TsinθTcosθ=qEmg
This simplifies to:
tanθ=qEmg(3)
Step 4: Substitute Values
Substituting the known values into equation (3):
- q=75μC=75×10−6C
- E=104N/C
- m=0.1kg
- g=10m/s2
Calculating:
tanθ=(75×10−6)(104)(0.1)(10)=0.751=0.75
Thus, θ=tan−1(0.75)≈36.87∘.
Step 5: Calculate the Radius of the Circle
The radius r of the circular motion can be found using:
r=lsinθ
Where l=10cm=0.1m.
Calculating:
r=0.1sin(36.87∘)=0.1×0.6=0.06m=6cm
Step 6: Calculate the Speed
The centripetal force required for circular motion is provided by the net force acting on the particle. The net force can be expressed as:
Fnet=Tsinθ+qEcosθ−mgcosθ
Setting this equal to the centripetal force mv2r:
mv2r=Tsinθ+qEcosθ−mgcosθ
From equation (1), we can express T as:
T=mgcosθ
Substituting T into the equation:
mv2r=mgsinθcosθ+qEcosθ−mgcosθ
Step 7: Solve for Speed v
Substituting the values:
0.1v20.06=0.1⋅10⋅0.750.6+(75×10−6)(104)(0.8)−0.1⋅10⋅0.6
Calculating each term:
1. Left side: 0.1v20.06=5v23
2. Right side:
- 0.1⋅10⋅0.750.6=1.25
- (75×10−6)(104)(0.8)=0.6
- 0.1⋅10⋅0.6=0.6
Putting it all together:
5v23=1.25+0.6−0.6=1.25
Thus,
5v2=3⋅1.25=3.75⟹v2=3.755=0.75⟹v=√0.75≈0.866m/s
Final Answers
- Radius of the circle: r=6cm
- Speed v≈0.866m/s
The forces acting on the particle are:
- Weight (mg) acting downward.
- Electric force (F_e = qE) acting horizontally due to the electric field.
- Tension (T) in the thread, which has components in both vertical and horizontal directions.
When the particle is in equilibrium (at rest), the following equations hold true:
Tcosθ=mg(1)
Tsinθ=qE(2)
Dividing equation (2) by equation (1) gives:
TsinθTcosθ=qEmg
This simplifies to:
tanθ=qEmg(3)
Substituting the known values into equation (3):
- q=75μC=75×10−6C
- E=104N/C
- m=0.1kg
- g=10m/s2
tanθ=(75×10−6)(104)(0.1)(10)=0.751=0.75
Thus, θ=tan−1(0.75)≈36.87∘.
The radius r of the circular motion can be found using:
r=lsinθ
Where l=10cm=0.1m.
r=0.1sin(36.87∘)=0.1×0.6=0.06m=6cm
The centripetal force required for circular motion is provided by the net force acting on the particle. The net force can be expressed as:
Fnet=Tsinθ+qEcosθ−mgcosθ
Setting this equal to the centripetal force mv2r:
mv2r=Tsinθ+qEcosθ−mgcosθ
T=mgcosθ
mv2r=mgsinθcosθ+qEcosθ−mgcosθ
Substituting the values:
0.1v20.06=0.1⋅10⋅0.750.6+(75×10−6)(104)(0.8)−0.1⋅10⋅0.6
1. Left side: 0.1v20.06=5v23
2. Right side:
- 0.1⋅10⋅0.750.6=1.25
- (75×10−6)(104)(0.8)=0.6
- 0.1⋅10⋅0.6=0.6
5v23=1.25+0.6−0.6=1.25
Thus,
5v2=3⋅1.25=3.75⟹v2=3.755=0.75⟹v=√0.75≈0.866m/s
- Radius of the circle: r=6cm
- Speed v≈0.866m/s
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.123videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.29videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
A charged particle of mass m=1 kg and charge q=2μC is thrown for a horizotal ground at an angle θ=45∘ with speed 20m/s. In space a horizontal electric field E=2×107 V/m exist. Find the range on horizontal ground of the projectile thrown.
View SolutionA small sphere of mass m=0.6kg carrying a positive charge q=80μC is connected with a light, flexible, and inextensible string of length r=30cm and whirled in a vertical circle. If a horizontal rightward electric field of strength E=105NC−1 exists in the space, calculate the minimum velocity of the sphere required at the highest point so that it may just complete the circle (g=10ms−2).
View Solution
Knowledge Check
- Question 1 - Select One
A positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
 A2qEm(√lg)BqEm(√lg)CqEm(√2lg)DqE2m(√lg)
A2qEm(√lg)BqEm(√lg)CqEm(√2lg)DqE2m(√lg) - Question 2 - Select One
A charged particle of mass m = 2 kg and charge 1μC is projected from a horizontal ground at an angle θ=45∘ with speed 10ms−1. In space, a horizontal electric field towards the direction of projection E=2×107NC−1 exists. The range of the projectile is
A20 mB60 mC200 mD180 m - Question 3 - Select One
A charged particle of mass m=2kg and charge 1μC is thrown from a horizontal ground at an angle of 45∘ with horizontal with a spedd of 10m/s. In space a horizontal electric field E=2×107N/C exists. Find the range of the projectile
 A5mB30mC10mD20m
A5mB30mC10mD20m
A particle of mass 2 kg chrge 1 mC is projected vertially with velocity k10ms−1. There is as uniform horizontal electric field of 104N/C, then
View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.View SolutionA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
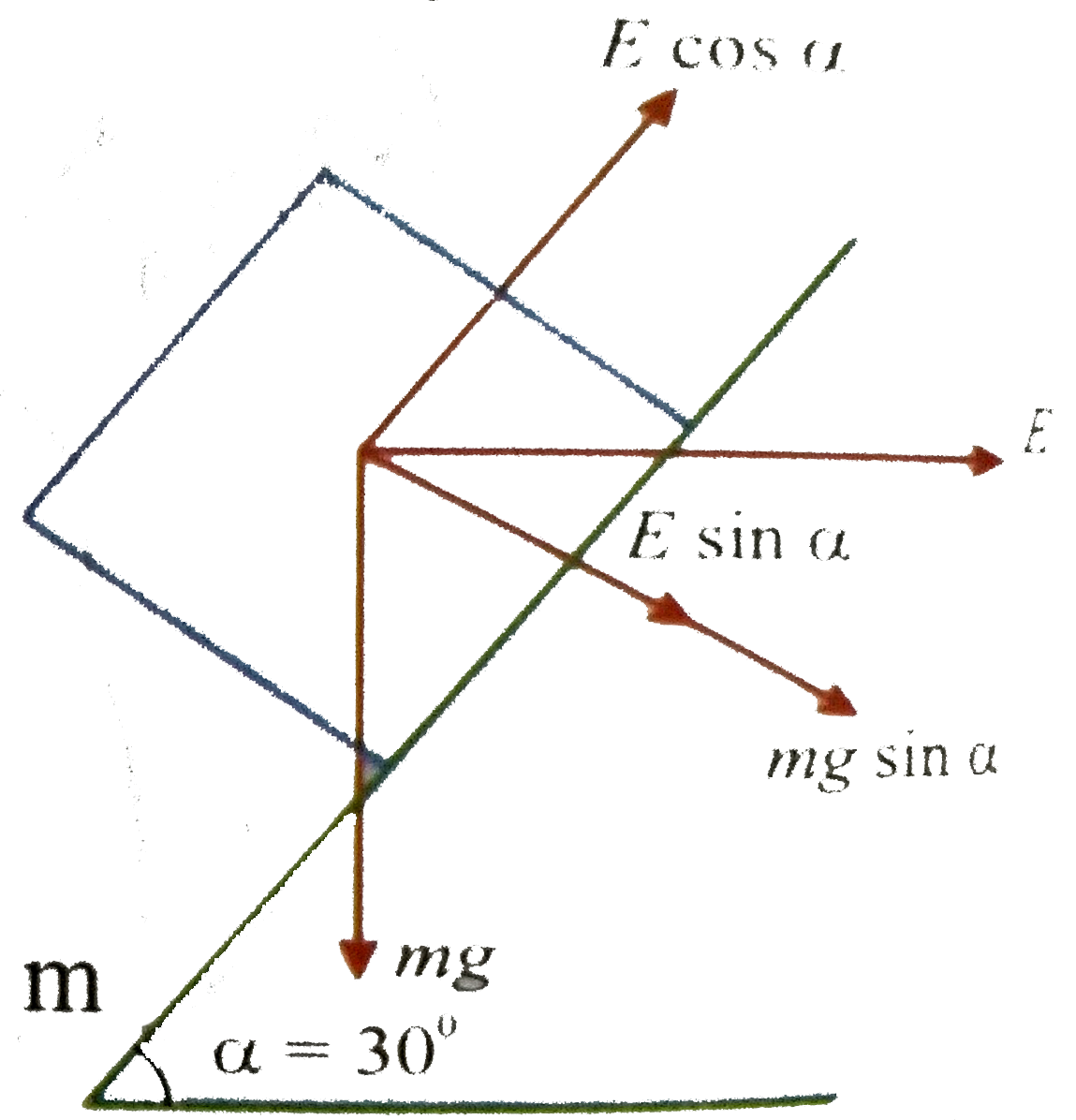
View SolutionA particles of mass 1kg and carrying positive charge 0.01C is sliding down an inclined plane of angle 30∘ with the horizontal .An electric field E is applied to stop the particles.If the coefficient of friction between the particles and the surface of the plane is 12√3. E must be
 View Solution
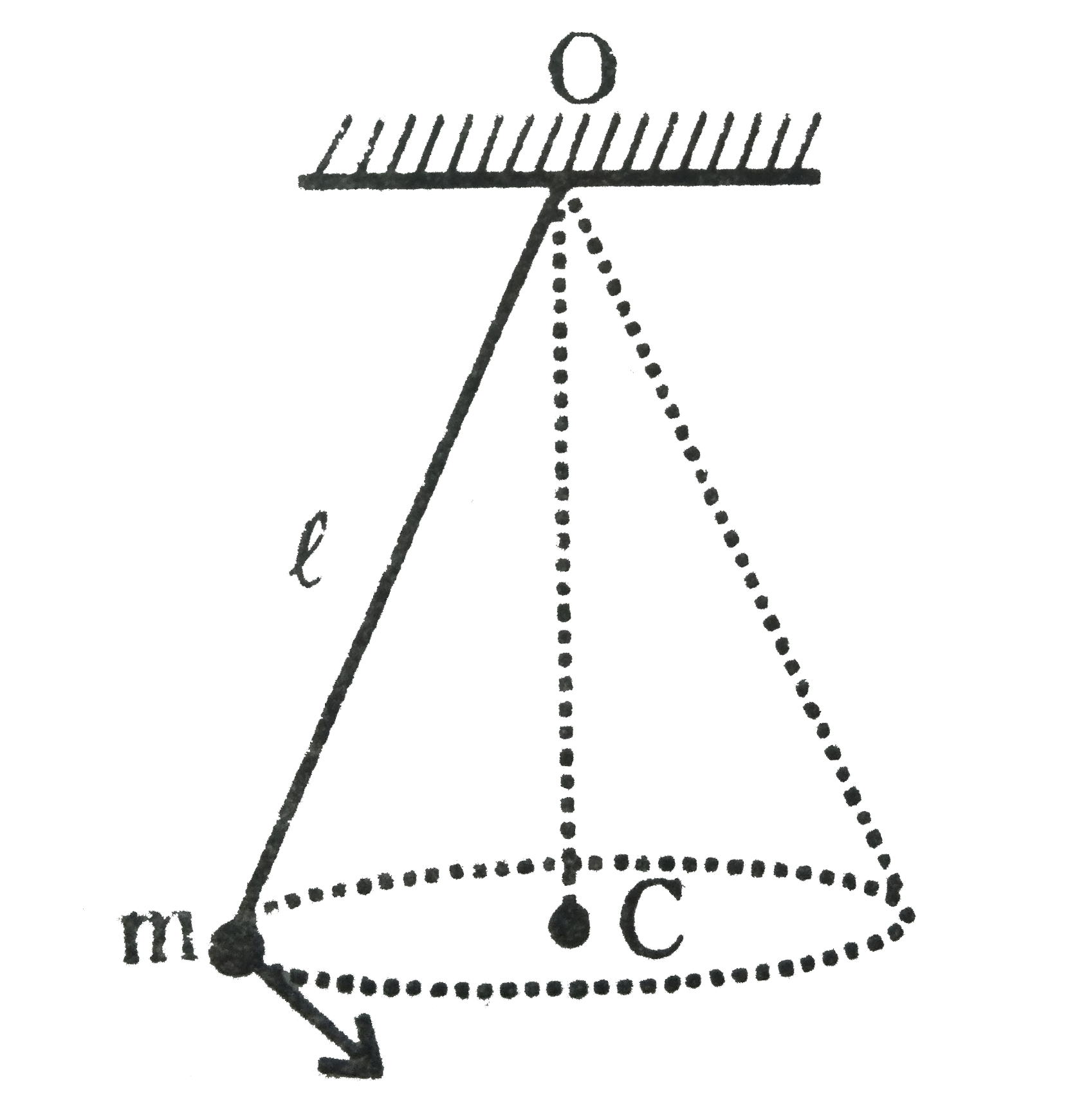
View SolutionA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
 .View Solution
.View Solution

