If you carry out the integral of the electric field ∫→E.→dl for a closed path like that as shown in (Fig. 3.40), the integral will always be equal tom zero, independent of the shape of the path and independent of where charges may be located relative to the path. Explain why.
 .
.
Vf−Vi=∫fi→E.dl
In a closed path, Vi=Vf. Hence,
∫fi→E.dl in a close path will be zero.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.29videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.39videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples9videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
In Fig. a "semi-infinite" nonconducting rod (that is, infinite in one direction only) has uniform linear charge density λ. (a) show that the electric field →Epat point P makes an angle 45∘ with the rod and that this result is independent of the distance R. (Hint : Separetly find the component of →Ep parallel to the rod and the component perpendicular to the rod.) (b) Find the the field magnitude for linear charge density 4.52 nC/m and R = 3.80 cm.
 View Solution
View SolutionA uniform electric field E axis between two charged plates as shown in Fig. What would be work done in moving a charge q along the closed recetangualr path ABCDA ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The line integral of magnetic field →B around any closed path through which current I is flowing is given by ∮c→B.→dl=
Aμ0I2Bμ0ICμ0IDIμ0 - Question 2 - Select One
Statement I: no electric current will be present within a region having uniform and constant magetic field.
Statement II: Within a region of unifrom and cinstant magnetic field →B, the path integral of magnetic field ∮→B.d→l along any closed path is zero. Hence, from Ampere cirauital law ∮→B.d→l=μ0I (where the given terms ahve usual meaning), no current can be present within a region having uniform and constant magnetic field .A(a) Statement I is True, Statement II is True, Statement II is correct expaination for Statement I.B(b) Statement I is True, Statement II is True, Statement II is NOT a correct expaination for Statement I.C( c) Statement I is True, Statement II is false.D( d) Statement I is False, Statement II is True. - Question 3 - Select One
A velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
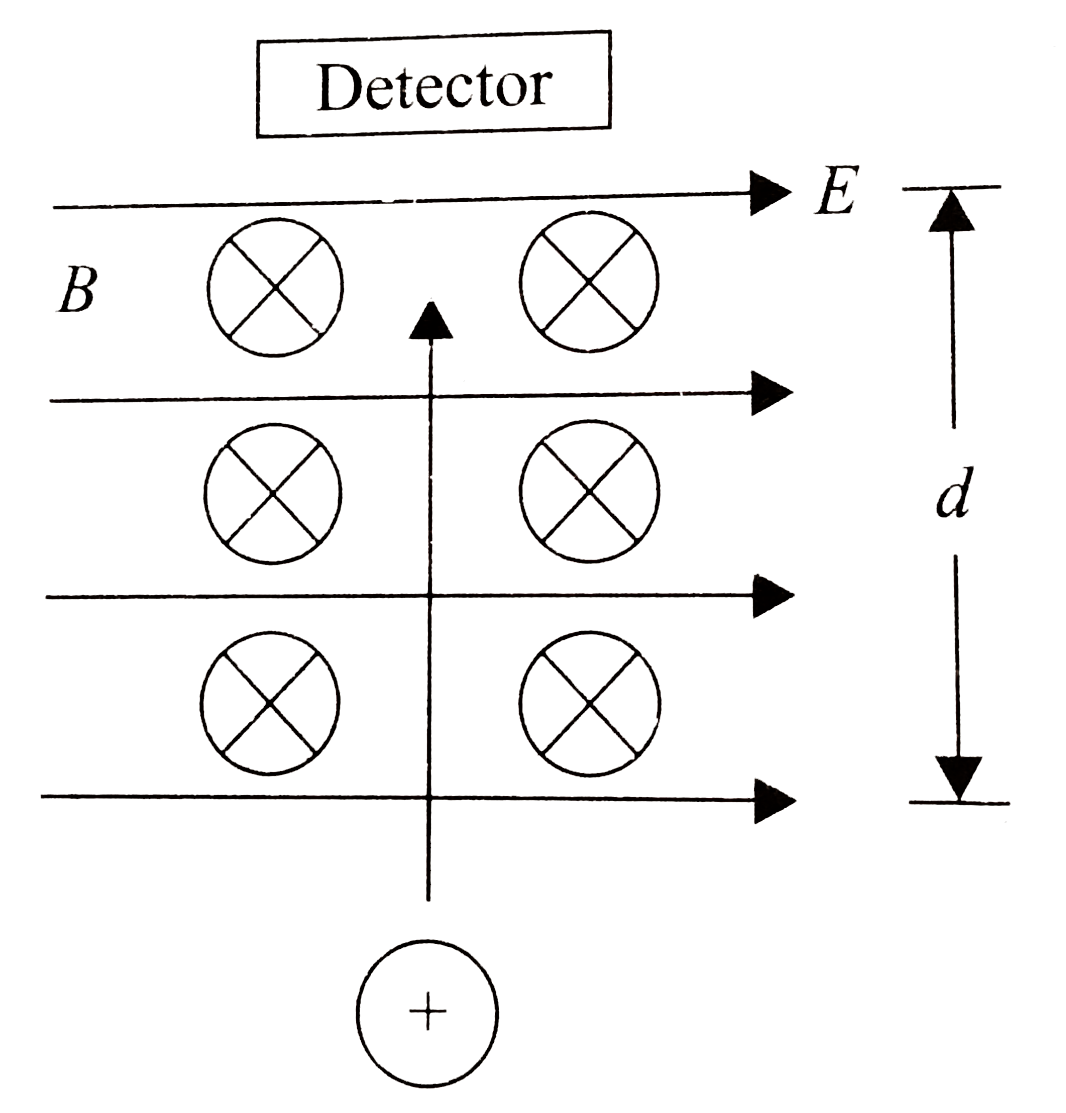
The moving particle will also experience a force due to magnetic field given by F = qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
Which of the following is true about the velocity filter shown in Fig,Ait would not work with negatively charged particles.Bwider the detector entrance, the narrower the range of speed detected.Cgreater the distance d, the narrower the range of speed detected.DThe detector may not detect a charged particles with desired filter speed if its charge is too high.
(a) A charge particle travelling along positive x direction with speed Vx enters a region of width having a uniform electric field E in positive y direction. A screen is kept, at a distance D(>>l) from the region of the field, in yz plane. Find the y co-ordinate of the point where the particle strikes the screen. Charge and mass of the par- ticle is + q and m respectively.
(b) The electric field in the region is replaced with a uniform magnetic field B in negative z direction. Now calculate the y co-ordinate of the point on the screen where the particle hits it. Assume deflection due to field to be small and D>>l.
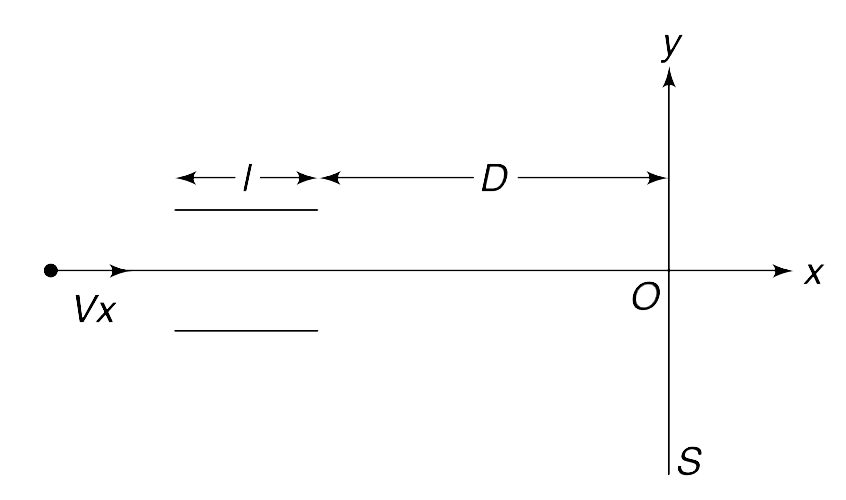
(c) Now the field region is filled with a uniform electric (E) and magnetic field (B) both directed in positive y direction. A beam of protons and some other positive ion enters the region trav- elling along x direction. The particles hit the screen along two curved paths. Explain. Draw the two curves in yz plane and point out which one represents the protons.View SolutionA uniform electric field E exists between two oppositely charged plates (Fig. 3.38). What will be the work done in moving a charge q along a closed rectangular path ?
 .View Solution
.View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
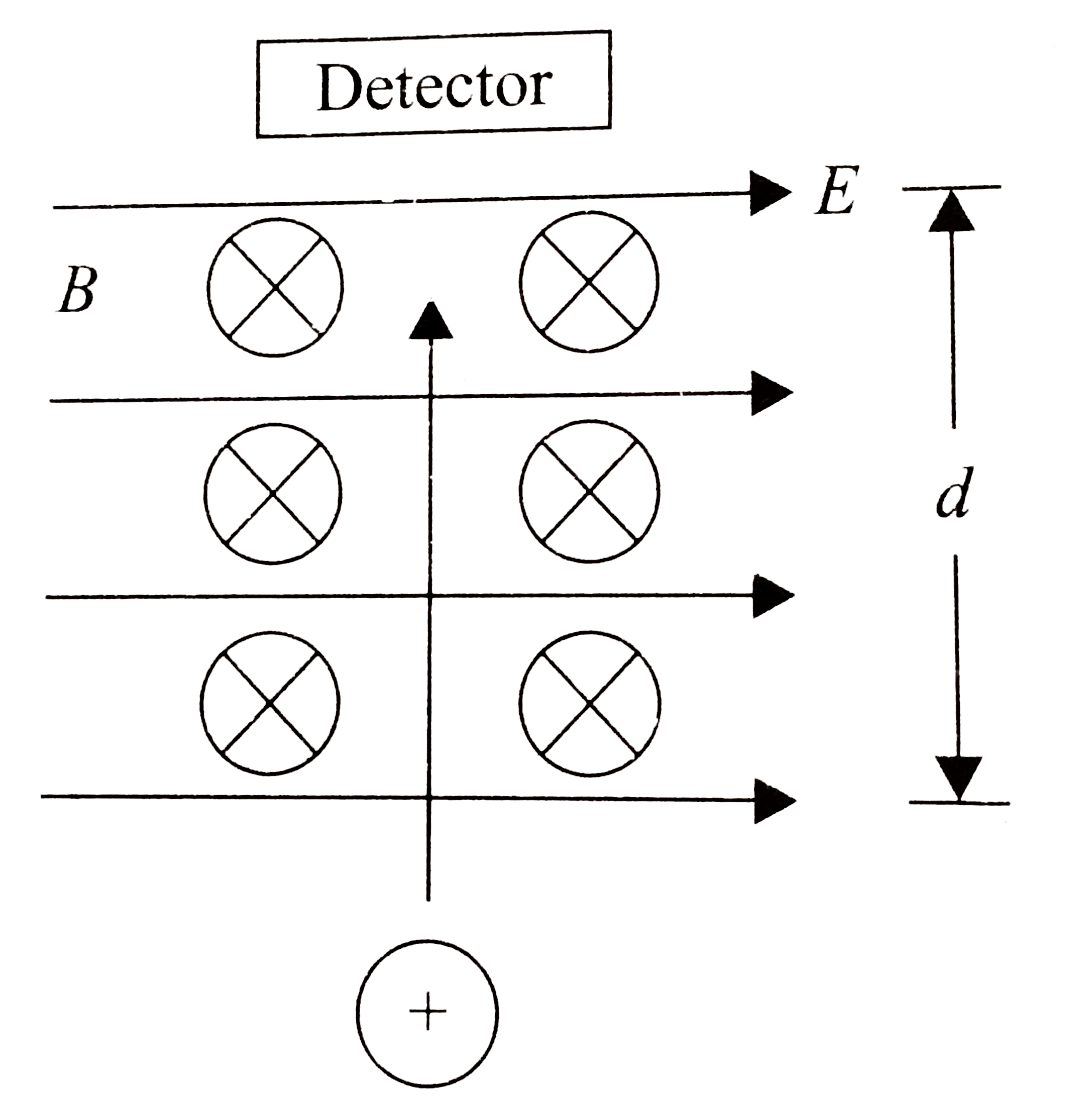
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
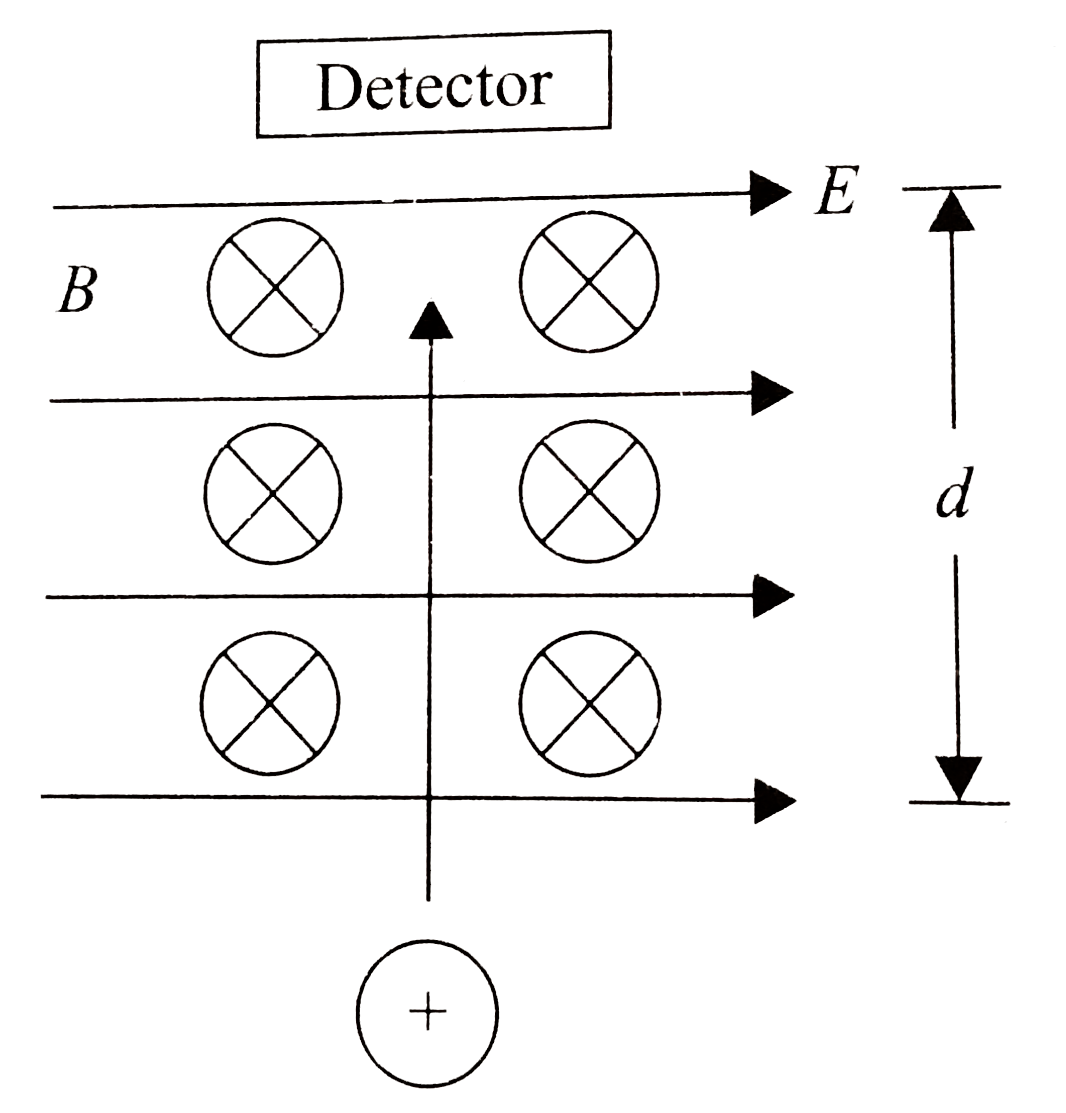
The moving particle will also experience a force due to magnetic field given by F = qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
If the filter is set to detect particles of speed v0, which one of the following diagrams best illustrates how the magnitude of the particle acceleration (a) depends on velocity v?View SolutionA uniform electric field E is created between two parallel charged plates as shown in figure . An electron enters the field symmetrically between the plates with a speed v0. The length of each plate is l. Find the angle of deviation of the path of the electron as it comes out of the field.
 View Solution
View Solution

