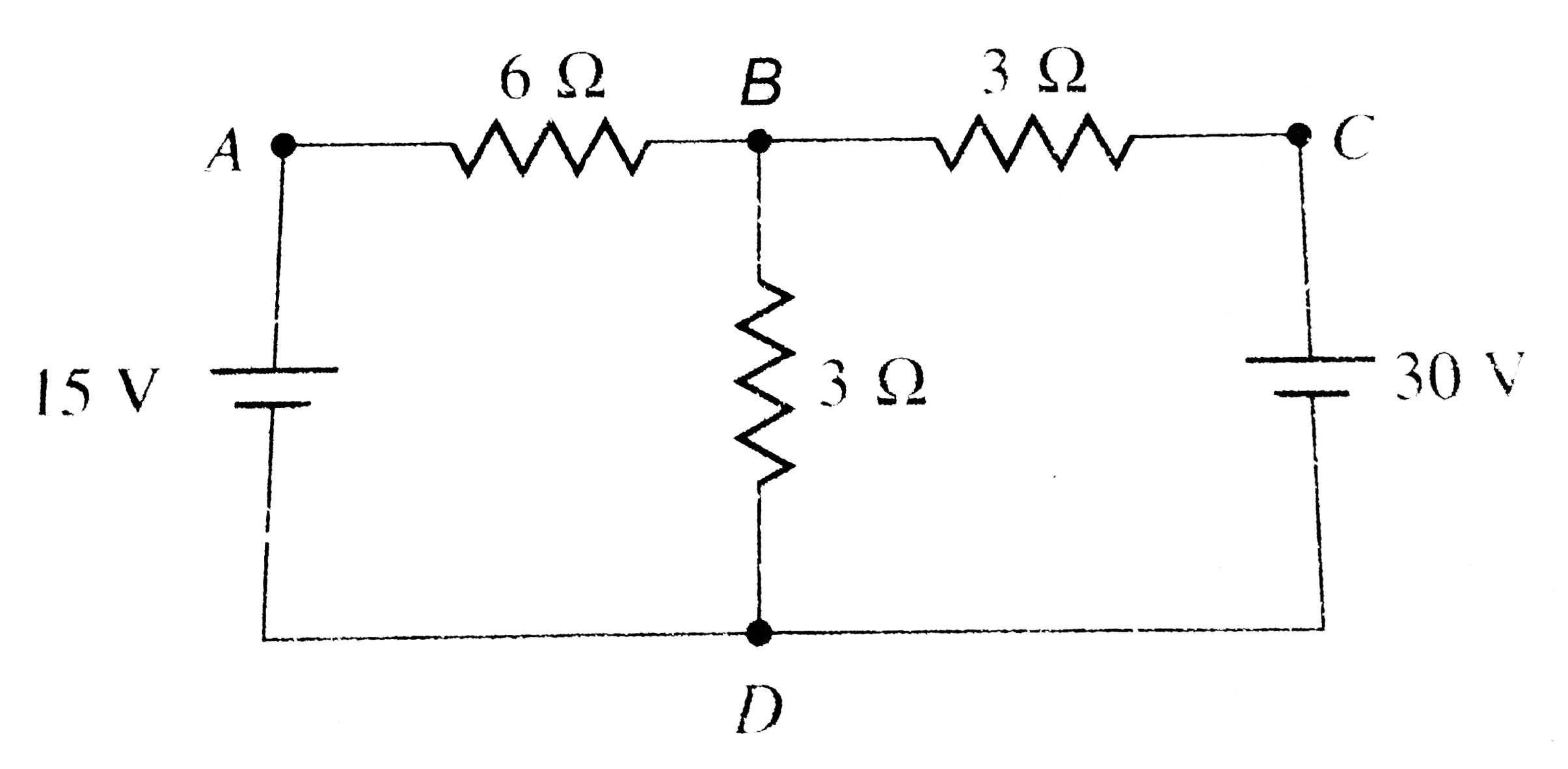
In the circuit shown in fig. find the current through the branch BD.
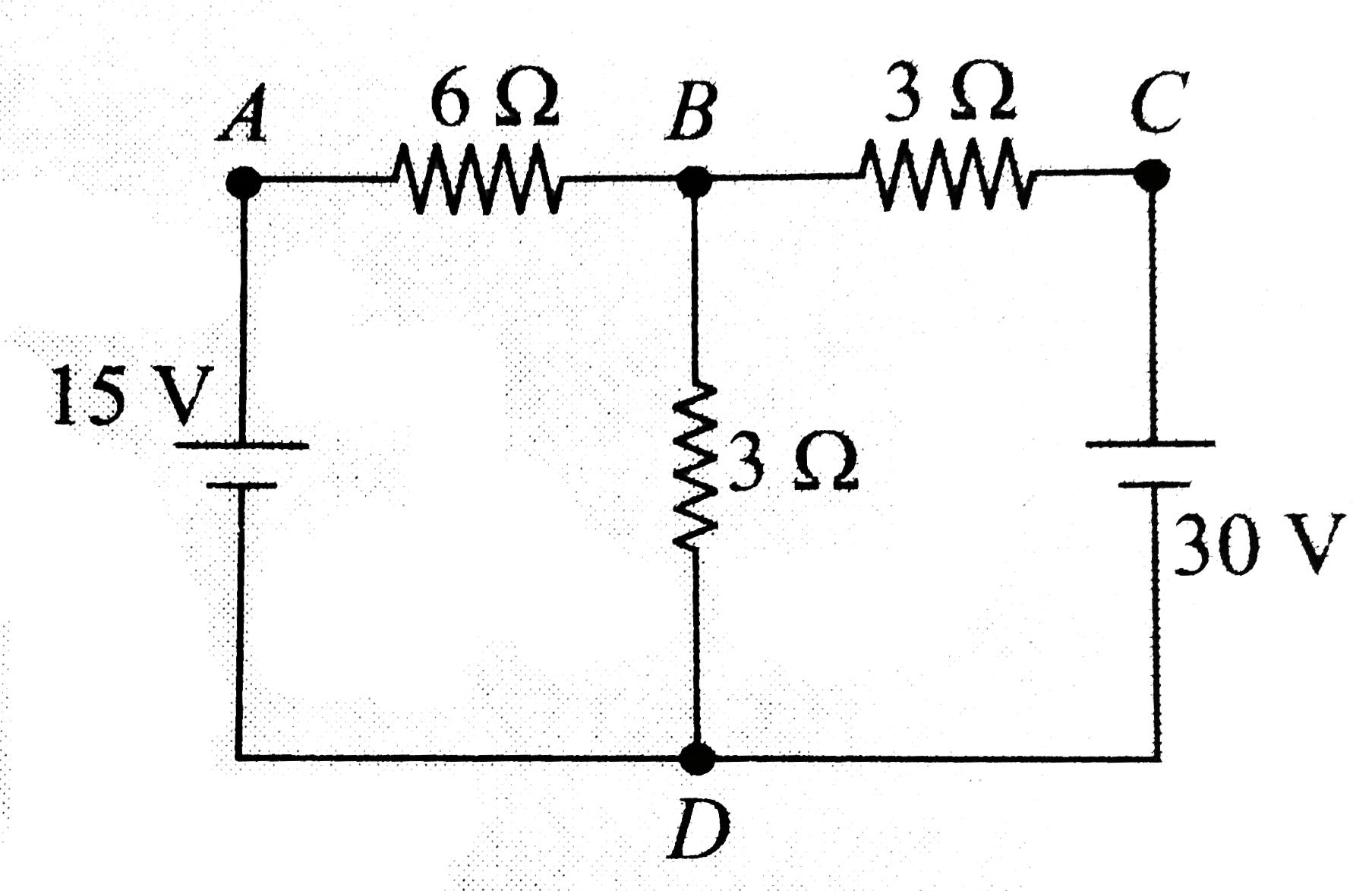
A
2 A
B
3 A
C
4 A
D
5 A
Video Solution
Text Solution
The correct Answer is:D
Method 1 : Using Kirchhoff's law M The currents in the circuit are assumed as shwon in fing Applying KVL along the loop ABDA, we get
−6i1−3i2+15=0
or 2i1+i2=5(i)
Applying KVL along the loop BCDB, we get
−3(i1−i2)−30+3I2=0
or −I1+2i2=10(ii)
Solving Eqs. (i) and (ii) for i2,we geti2=5A.
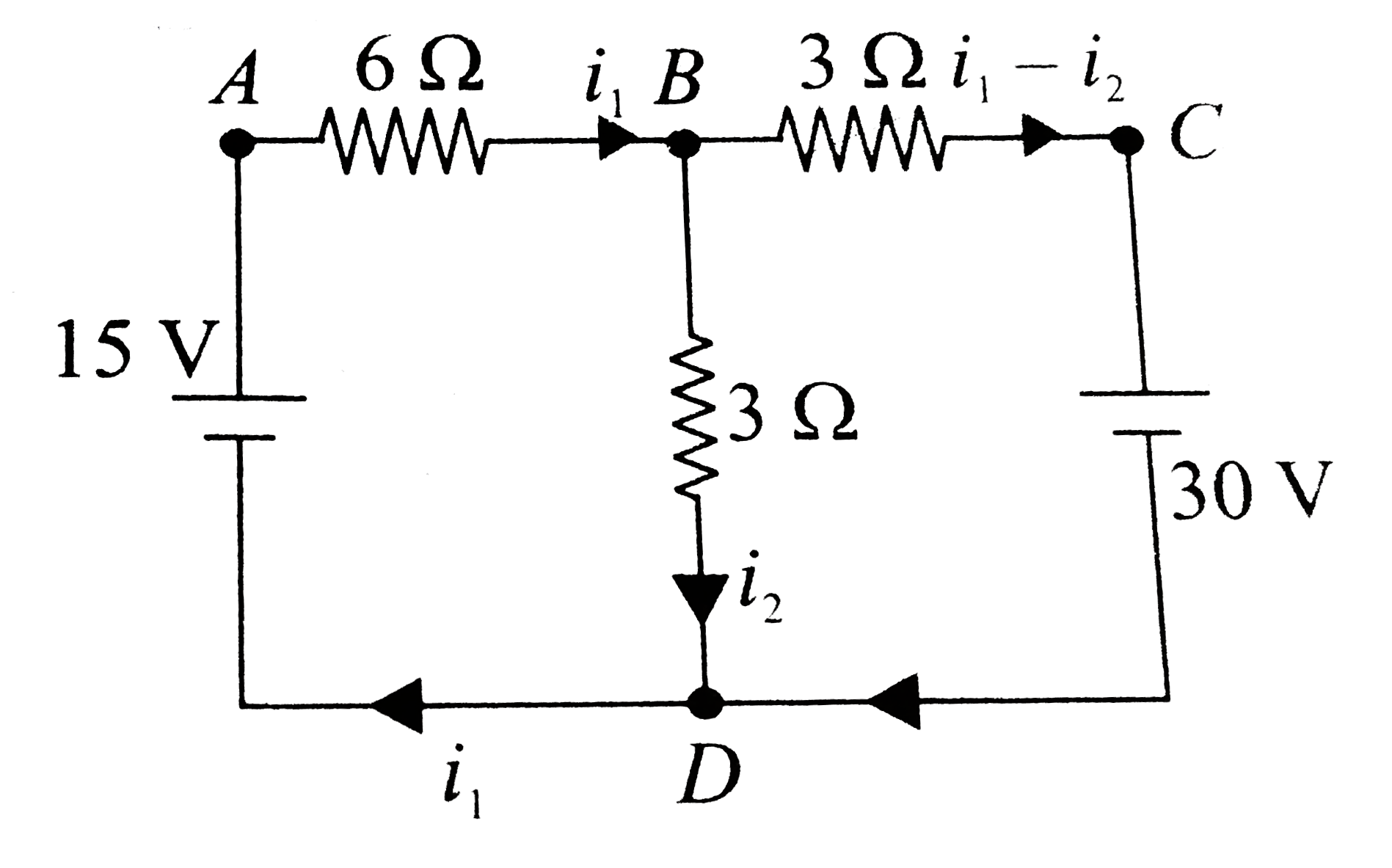
Method 2: using equivalnet battery method (i)
we can treat 6Ωand3Ω resistance connected with 15V
and 30V batteries, respectively, as internal resistances of the
batteries. Now we can assume these batteries are connected in
parallel, and equivalnet battery of these two is connected with
resistance connected across B and D.
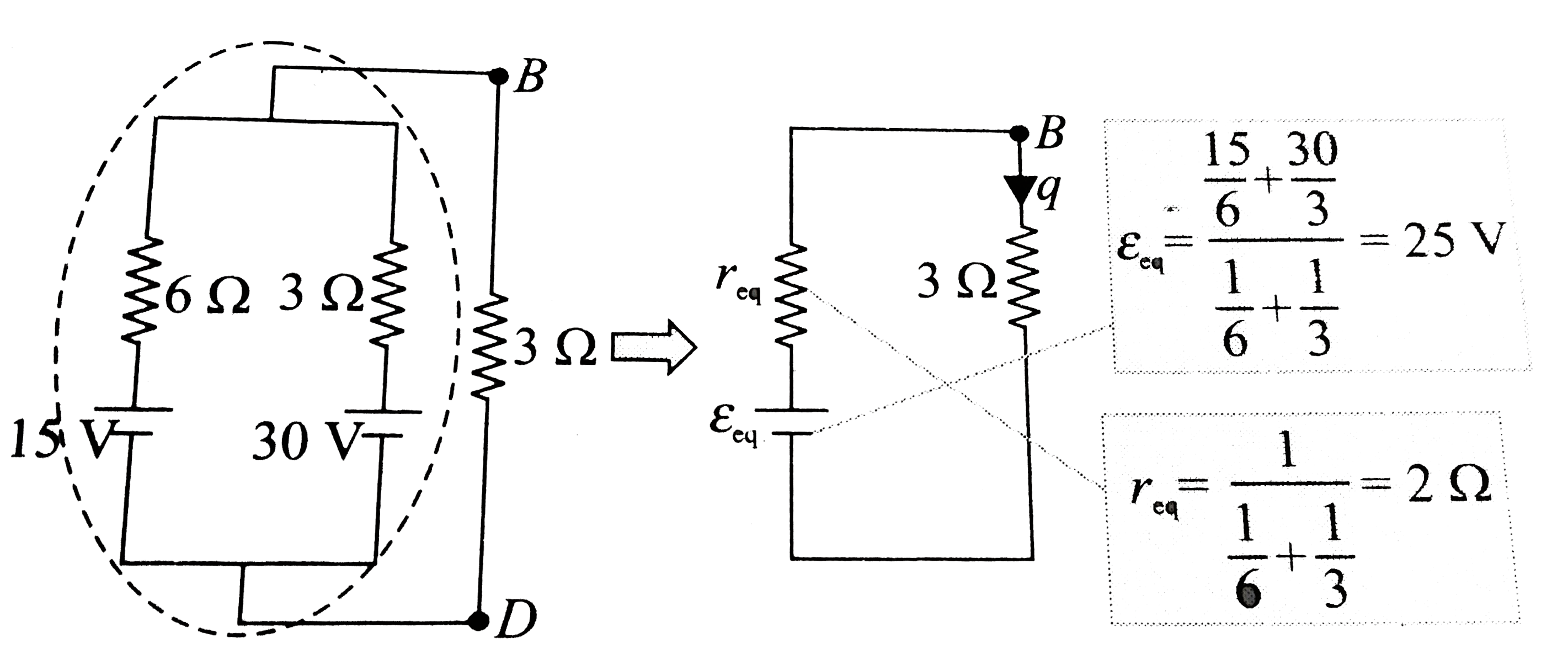
Hence, current through resistace connected across B and
D is
i=202+3=5A
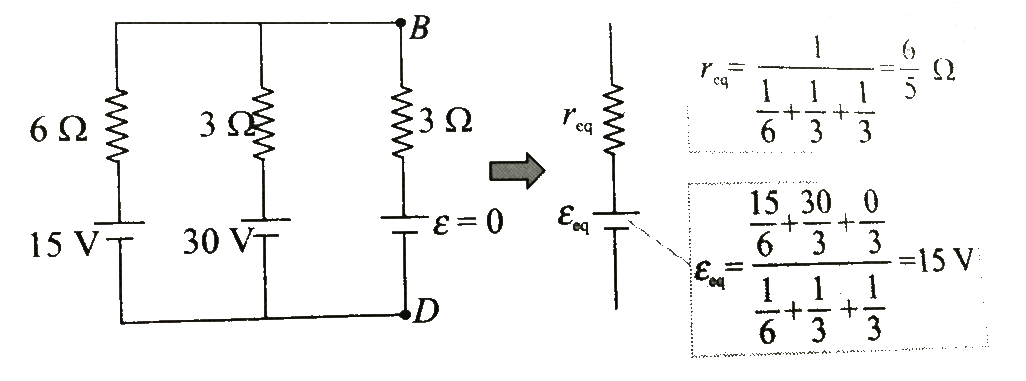
Method 3: Using equivalent battery method (ii)
We cna assume a battery of zero emf is connected in series
with resistance connected across BD. This resistance can be
treated as internal resistance of zero emf battery. Now we have
three battery which is the open cirucuit.
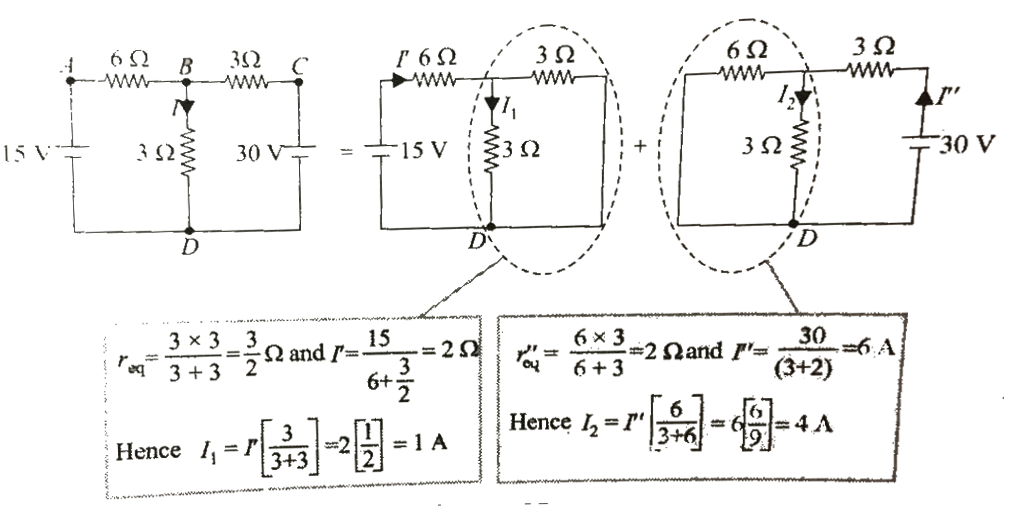
As equivalent battery in as open circuit, the potential
difference across each of the battery branch wikll be 15V.
Hence, current through the resistacne connected across BD is
I=1503=5A
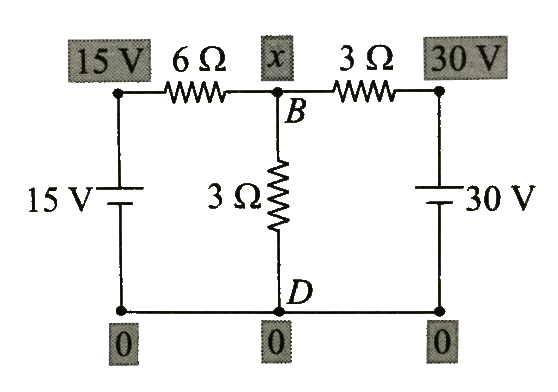
Method 4 : Using nodal method
Let us asume the potential of node D zero and the potential of node B x. then we can assign the potentials at different nodes
as shown in fig 5.124. At node B,
Hence current through resistacne connected across BD is
i=15−03=5A(fromB→D)

Method 5: using superposition principle In superposition method, we can take the effect of one battery at a time. From fig, it is clear that the effect on two
batteries can be taken by adding the effect of individual batteries.



|
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Knowledge Check
In the circuit shown in figure, find the current through the branch BD.
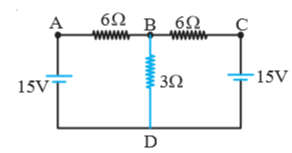 A1AB2.5AC3AD5A
A1AB2.5AC3AD5AIn the circuit shown in figure the current through
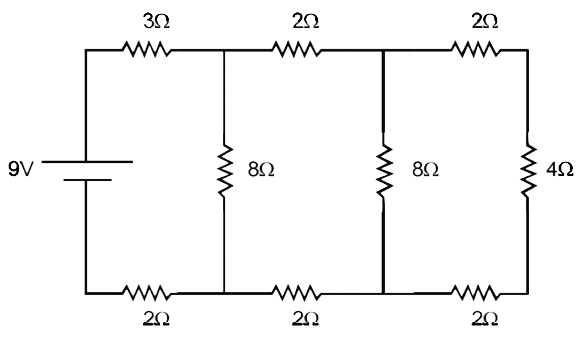 Athe 3Ω resistor is 0.50 A.Bthe 3Ω resistor is 0.25ACthe 4Ω is 0.50ADthe 4Ω resistor is 0.25A.
Athe 3Ω resistor is 0.50 A.Bthe 3Ω resistor is 0.25ACthe 4Ω is 0.50ADthe 4Ω resistor is 0.25A.In the circuit shown in the figure, the current through
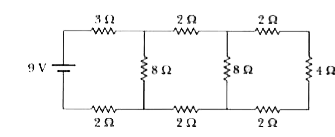 AThe 3Ω resistor is 0.50ABThe 3Ω resistor is 0.25ACThe 4Ω resistor is 0.50ADThe 4Ω resistor is 0.25A
AThe 3Ω resistor is 0.50ABThe 3Ω resistor is 0.25ACThe 4Ω resistor is 0.50ADThe 4Ω resistor is 0.25A
In the circuit shown , find the current through resistors.

View SolutionIn the circuit shown in figure ,
a. find the current is each branch
b. find the potential difference Vab of point a relative to point b.
View SolutionIn the circuit shown in figure. 3.82 find the current through battery and current in 8Ω resistances.
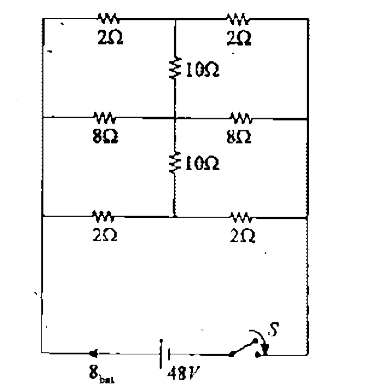
View SolutionIn the circuit shown,find the current through the Zener diode.
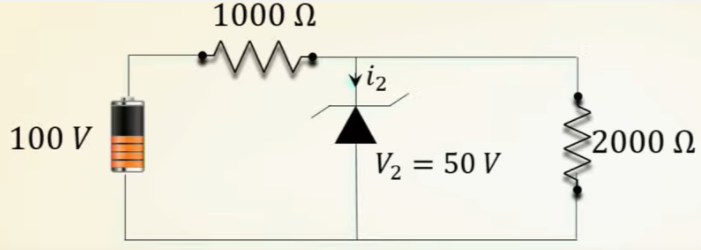
View Solution
In the circuit shown in the figure, the current through
View Solution