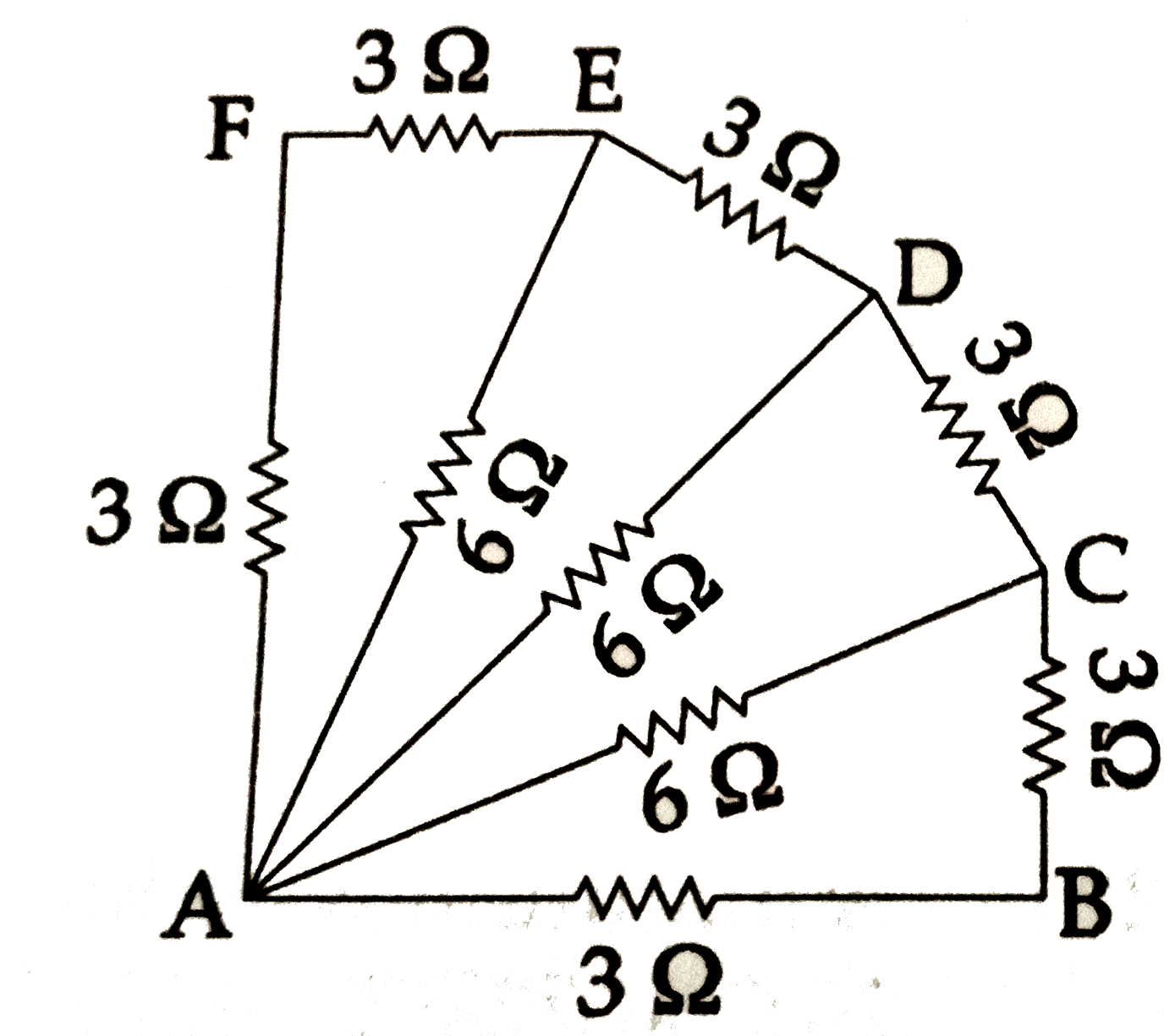
In previous illustration, find the equivalent resistance of the network between 1 and 2.
Video Solution
Text Solution
From symmetry, it si clear the current in
resistors connected between points (1 and 8) and (1 and 4)
should be same hecne points 4 and 8 are equipotential points.
Similarly, the current in resistor connected between points
(2 and 7) and (2 and 3) should be same, hence points 3 and 7
are equipotential points.
We can join points (4 and 8) and (3 and 7). we can redraw
the cirucit and calculate the equivalent resistance as shown in
fig. 5.128
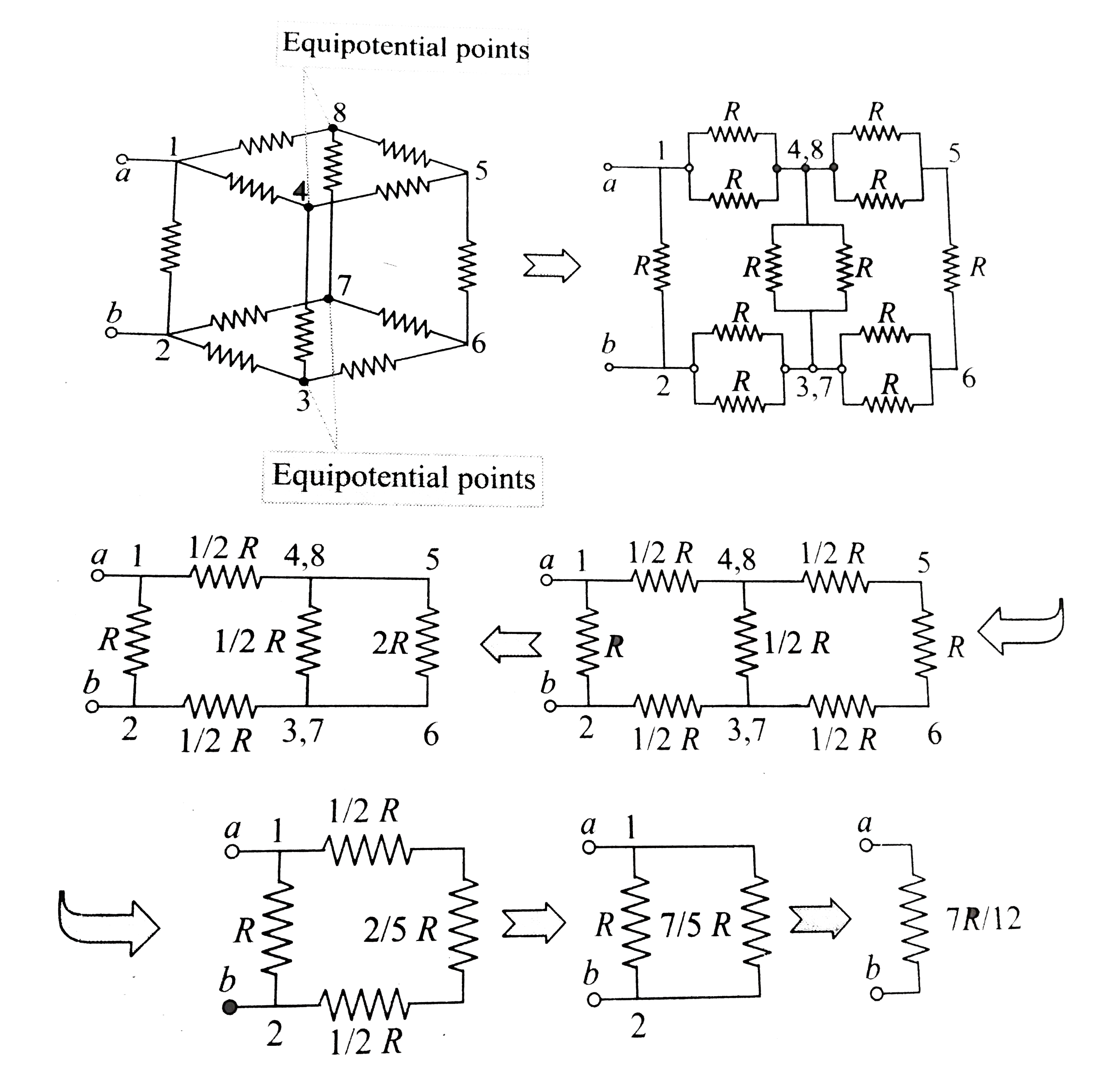
 <br> Method 2 : Let a current i enter the point a and leave the point <br> b. From symmetry we can distribute currents in different <br> resistors as shwon in fig. <br> From KCL, we have <br> <span class=) i=i1_1+2i2
i=i1_1+2i2
Applying KVL for the loop (1→4→3→2→1), we have
−i2R−i3R−i2R+i1R=0
or i1=2i2+i3(ii)
Applying KVL for the loop (4→3→6→5→4), we have
−i3R+(i2−i3)R+2(i2−i3)R+(i2−i3)R=0
or 4i2−5i3=0(iii)
On solving Eqs. (i), (ii) and (iii), we get
i1=712i,i2=524i,i3=16i
The potential differecne across (1→2)isi1R=712Ir. The
potential difference across equivalent resistance is iReq. Thus
iReq=712iRorReq=712R
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Knowledge Check
- Question 1 - Select One
Equivalent resistance of the given network between points A and B is
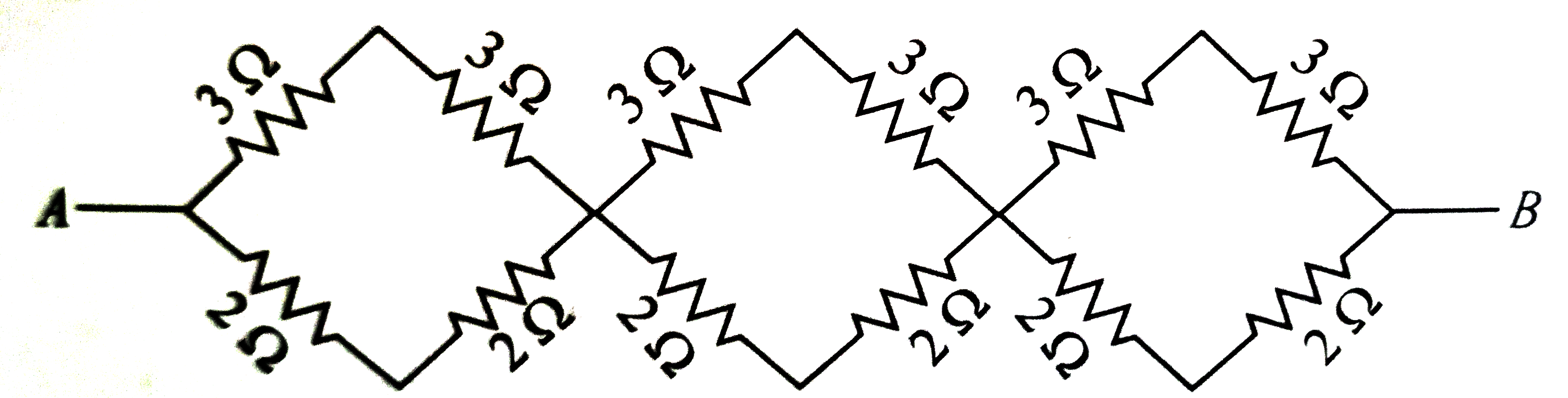 A31/5ΩB41/5ΩC36/5ΩD49/5Ω
A31/5ΩB41/5ΩC36/5ΩD49/5Ω
Find the equivalent resistances of the network shown in figurebetween the points a and b.
 View Solution
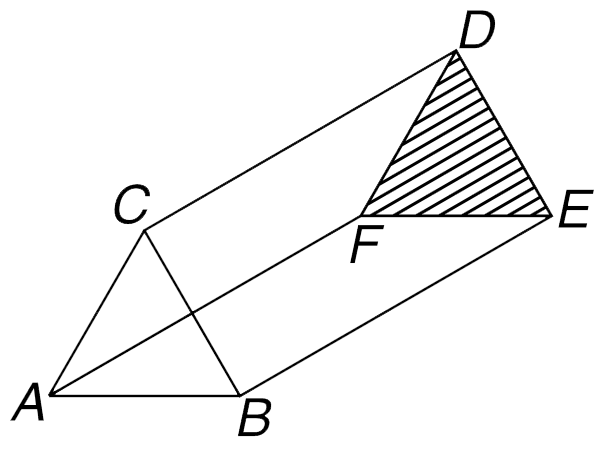
View SolutionA prism shaped network of resistors has been shown in the figure. Each arm (like AB, AC, CD, DF ...) has resistance R. Find the equivalent resistance of the network between
(a) A and B
(b) C and D
 View Solution
View Solutionfind the equivalent resistance between A and B.
 View Solution
View SolutionFind the equivalent resistance of the networks shown in figure between the points A and B
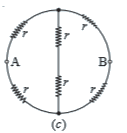 View Solution
View SolutionFind the equivalent resistance between A and B
 View Solution
View SolutionFind the equivalent resistance between A and B
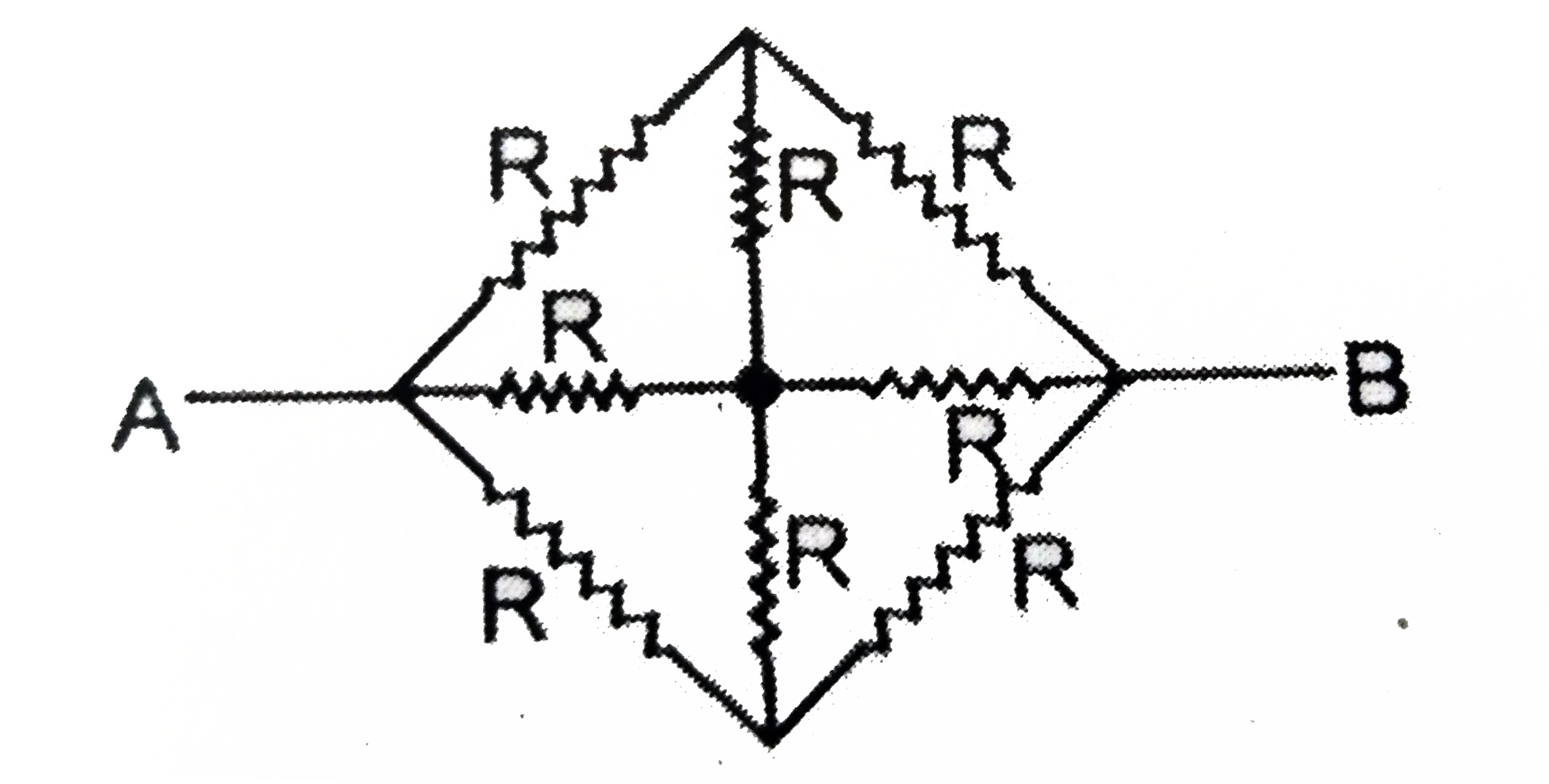 View Solution
View SolutionFind the equivalent resistance between a and B
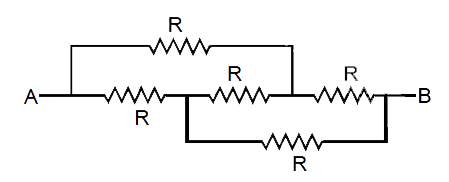 View Solution
View Solution