The current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
To calculate the current flowing through a cylindrical conductor with a varying current density, we can follow these steps:
Step 1: Understand the Current Density Equation
The current density J is given by the equation:
J=J0(1−rR)
where:
- J0 is the maximum current density at the center of the conductor (when r=0),
- R is the radius of the conductor,
- r is the distance from the central axis.
Step 2: Define the Differential Area Element
To find the total current, we need to integrate the current density over the cross-sectional area of the conductor. The differential area element dA in cylindrical coordinates can be expressed as:
dA=2πrdr
This represents a thin ring of radius r and thickness dr.
Step 3: Express the Current in Terms of Current Density
The current dI flowing through the differential area dA is given by:
dI=JdA
Substituting the expressions for J and dA:
dI=J0(1−rR)(2πrdr)
Step 4: Integrate to Find Total Current
To find the total current I, we need to integrate dI from r=0 to r=R:
I=∫R0dI=∫R0J0(1−rR)(2πrdr)
Step 5: Simplify the Integral
Now, we simplify the integral:
I=2πJ0∫R0(r−r2R)dr
This can be split into two separate integrals:
I=2πJ0(∫R0rdr−1R∫R0r2dr)
Step 6: Calculate the Integrals
Calculating the first integral:
∫R0rdr=(r22)R0=R22
Calculating the second integral:
∫R0r2dr=(r33)R0=R33
Step 7: Substitute Back into the Current Equation
Substituting these results back into the equation for I:
I=2πJ0(R22−1R⋅R33)
I=2πJ0(R22−R23)
Step 8: Combine the Terms
Finding a common denominator (which is 6):
I=2πJ0(3R26−2R26)=2πJ0(R26)
I=πJ0R23
Final Answer
Thus, the total current I flowing through the cylindrical conductor is:
I=πJ0R23
The current density J is given by the equation:
J=J0(1−rR)
where:
- J0 is the maximum current density at the center of the conductor (when r=0),
- R is the radius of the conductor,
- r is the distance from the central axis.
To find the total current, we need to integrate the current density over the cross-sectional area of the conductor. The differential area element dA in cylindrical coordinates can be expressed as:
dA=2πrdr
This represents a thin ring of radius r and thickness dr.
The current dI flowing through the differential area dA is given by:
dI=JdA
Substituting the expressions for J and dA:
dI=J0(1−rR)(2πrdr)
To find the total current I, we need to integrate dI from r=0 to r=R:
I=∫R0dI=∫R0J0(1−rR)(2πrdr)
Now, we simplify the integral:
I=2πJ0∫R0(r−r2R)dr
This can be split into two separate integrals:
I=2πJ0(∫R0rdr−1R∫R0r2dr)
Calculating the first integral:
∫R0rdr=(r22)R0=R22
Calculating the second integral:
∫R0r2dr=(r33)R0=R33
Substituting these results back into the equation for I:
I=2πJ0(R22−1R⋅R33)
I=2πJ0(R22−R23)
Finding a common denominator (which is 6):
I=2πJ0(3R26−2R26)=2πJ0(R26)
I=πJ0R23
Thus, the total current I flowing through the cylindrical conductor is:
I=πJ0R23
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.2
50 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
The current density in a cylindrical conductor of radius R varies according to the equation J=J0(1−rR), where r=distacnce from the axis. Thus the current density is a maximum J0 ata the axis r=0 and decreases linealy to zero at the srface r=2√π. Current in terms of J0 is given by n(J06) then value of n will be.
View SolutionSuppose that instead the current density is a maximum J0 at the surface and decreases linearly to zero at the axis so that J=J0rR. Calculate the current.
View Solution
Knowledge Check
A cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
AπJ0R22B2πJ0R23C4πJ0R23Dnone of theseThe current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r)=J0(1−rR) . The total current in the radial regon r = 0 to r=R4 will be :
A5J0πR232B5J0πR296C3J0πR264DJ0πR3128A cylindrical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
A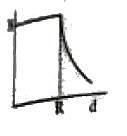 B
B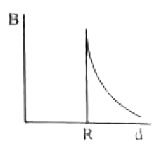 C
C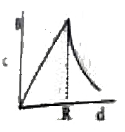 D
D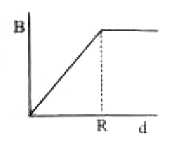
A current is flowing through a cylinderical conductor of radius R, such that current density at any cross-section is given by J=J0(1−rR), where r is radial distance from axis of the cylinder .Calculate the total current through the cross-section of the conductor.
View SolutionIf the current density in a linear conductor of radius 'a' varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) r<a and (ii) r>a.
View SolutionSuppose that the current density in a wife of radius a varies with r according to J=Kr2, where K is a constant and r is the distance from the axis of the wire. Find the megnetic field at a point distance r from the axis when (a) r < a and (b) r > a

View SolutionThe mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
View SolutionA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
View Solution
