Let V and I respresent, respectively, the readings of the voltmeter and ammetre shows in Fig. 6.34, and let RV and RV be their equivalent resistances. Because of the resistances of the meters, the resistnce R is not simply equal to V/I.
(a) When the circuit is connected as shows in Fig. 6.34 (a), shows that R=VI−RA
Explain why the true resistance R is always less than V/I.
(b) When the connections are as shows in Fig.6.34 (b)
Show that R=VI−(V/RV)
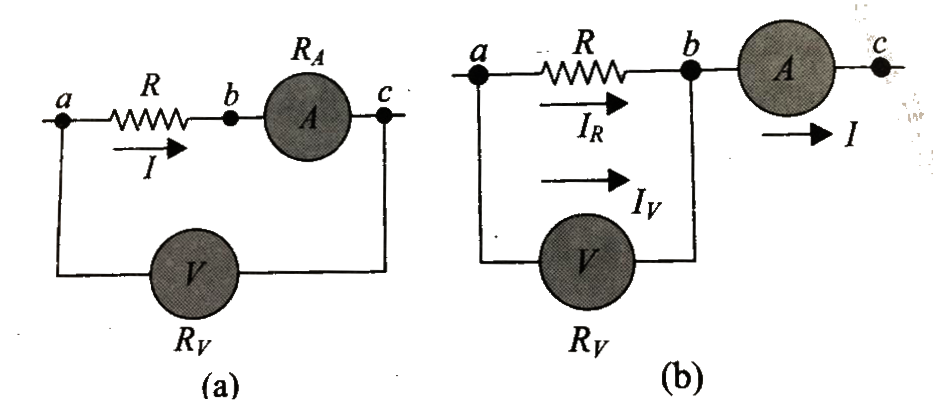
Explain why the true resistance R is always greater than V/I.
(c ) Show that the power delivered to the resistor in part
(i) is IV−I2RA and that in part (ii) is IV−(V2/RV)
V=IR+IRA or R=VI−RA
The true resistance R is always less then the reading (V/I) because in the circuit, the ammeter's resistance causes the current to be less than the actual. Thus, the smaller current required resistance R to be calculated larger than what it should be.
(b) I=VR+VRV or R=VRVIRV−V=VI−V/RV
Now the current measured is greater than that through the resistor, so R=V/IR is always greater than V/I.
(c ) (i) P=I2R=I2(V/I−RA)=IV−I2RA
(ii) P=V2/R=V(I−V/RV)=IV−V2/RV
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Single Correct
94 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Multiple Correct
7 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Exercise 6.1
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
Similar Questions
The ammeter A reads 2A and the voltmeter V reads 20V, the value of resistance R is (Assuming finite resistance's of ammeter and voltmeter)
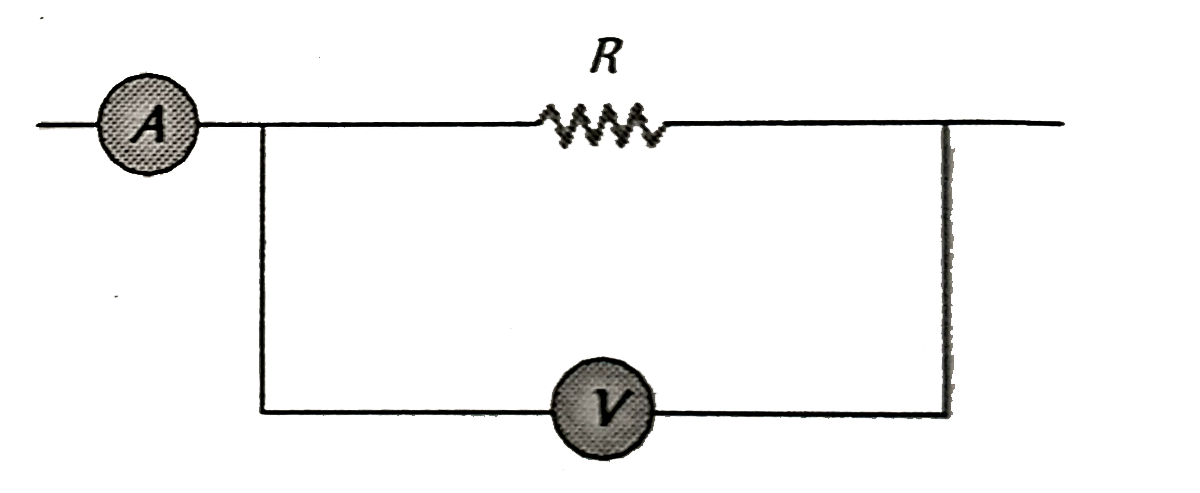
View SolutionThe voltmeter V in the figure. Reads 117V and the ammeter A reads 0⋅13A. The resistance of the voltmeter is 9000Ω and the resistance of ammeter is 0⋅015Ω. Compute (i) the resistance R, (ii) the power input to R.
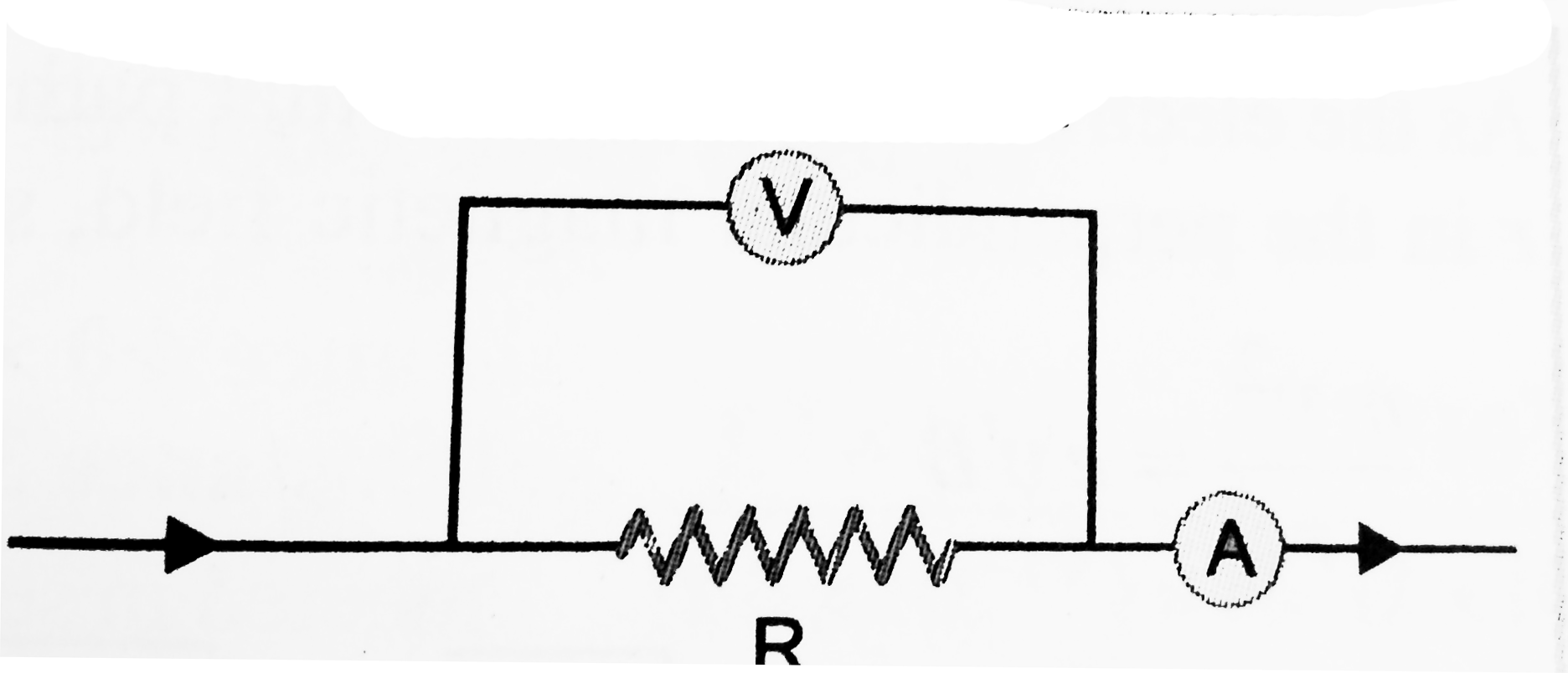
View Solution
Knowledge Check
Let V and I be the readings of the voltmeter and the ammeter respectively as shown in the figure. Let RV and RA be their corresponding resistancce Therefore,
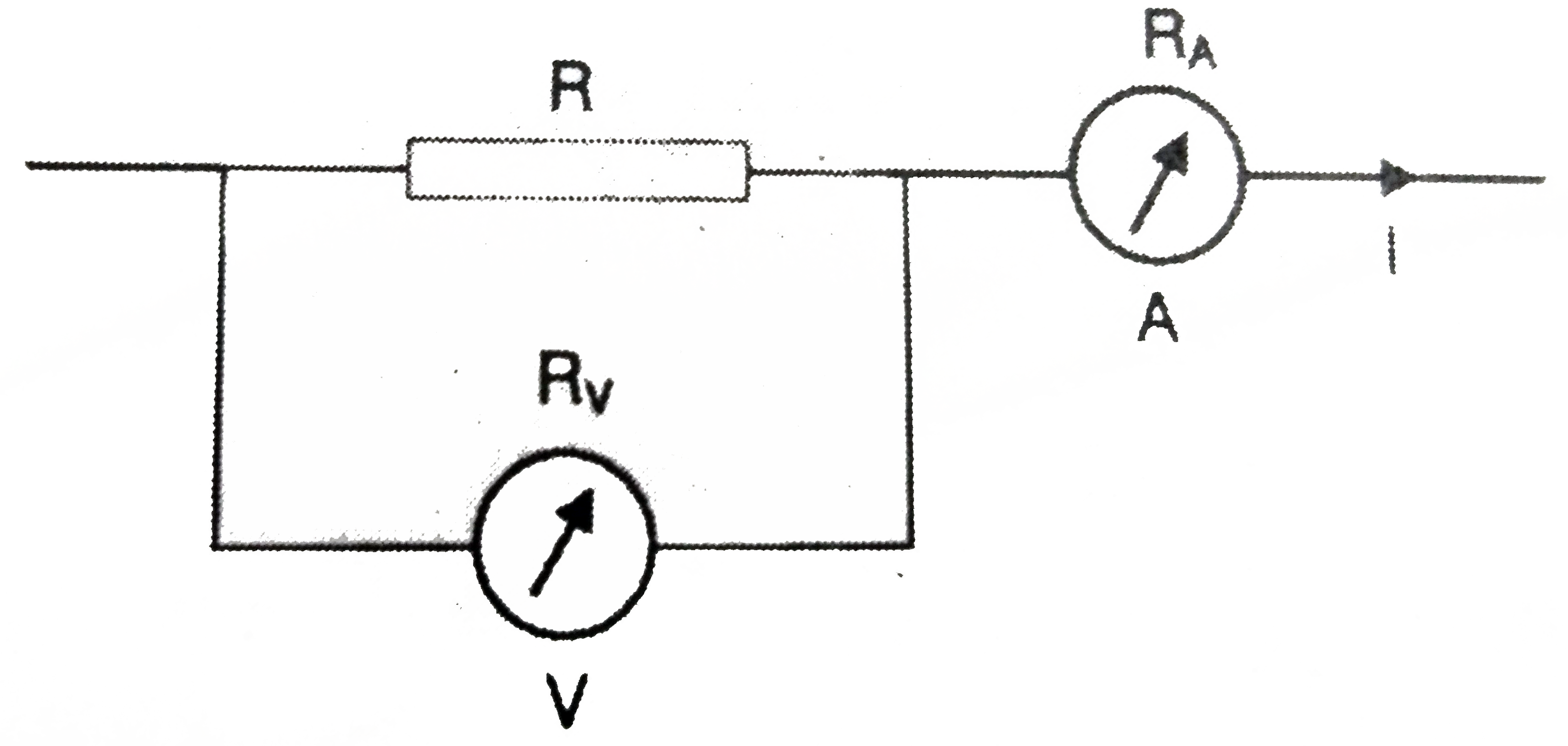 AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRA
AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRAIn the circuit shows in Fig. 6.42, resistors X and Y, each with resistance R, are connected to a 6V battery of negligible internal resistance. A voltmetre, also of resistance R, is connected across Y.
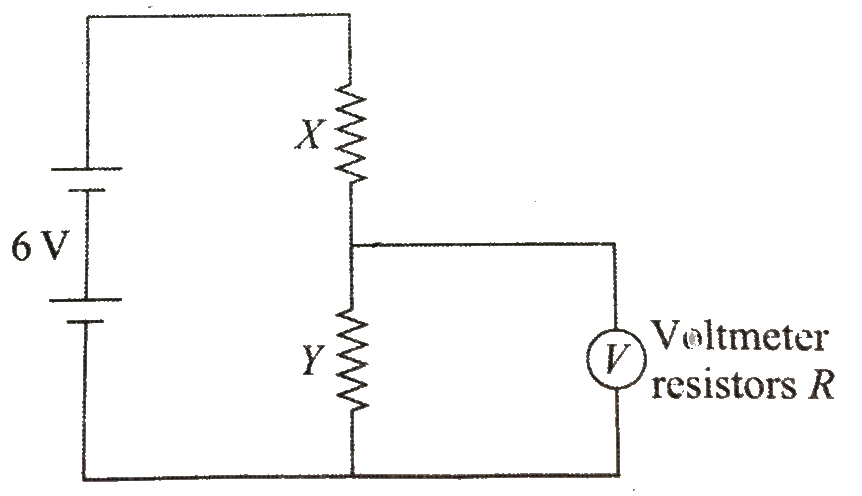
What is the reading of the voltmeter?AzeroBbetween0and3 VC3VDbetween3 Vand6 VAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
ABoth A and V will increaseBBoth A and V will decreaseCA will decrease and V will increaseDA will decrease and V will decrease
A 150 V voltmeter has a resistance of 20,000Ω when connected in series with a large resistance R across a 110-volt line the meter reads 5V. Find the resistance R.
View SolutionIn the circuit shown below, the ammeter and the voltmeter readings are 3 A and 6 V respectively . Then, the value of the resistance R is
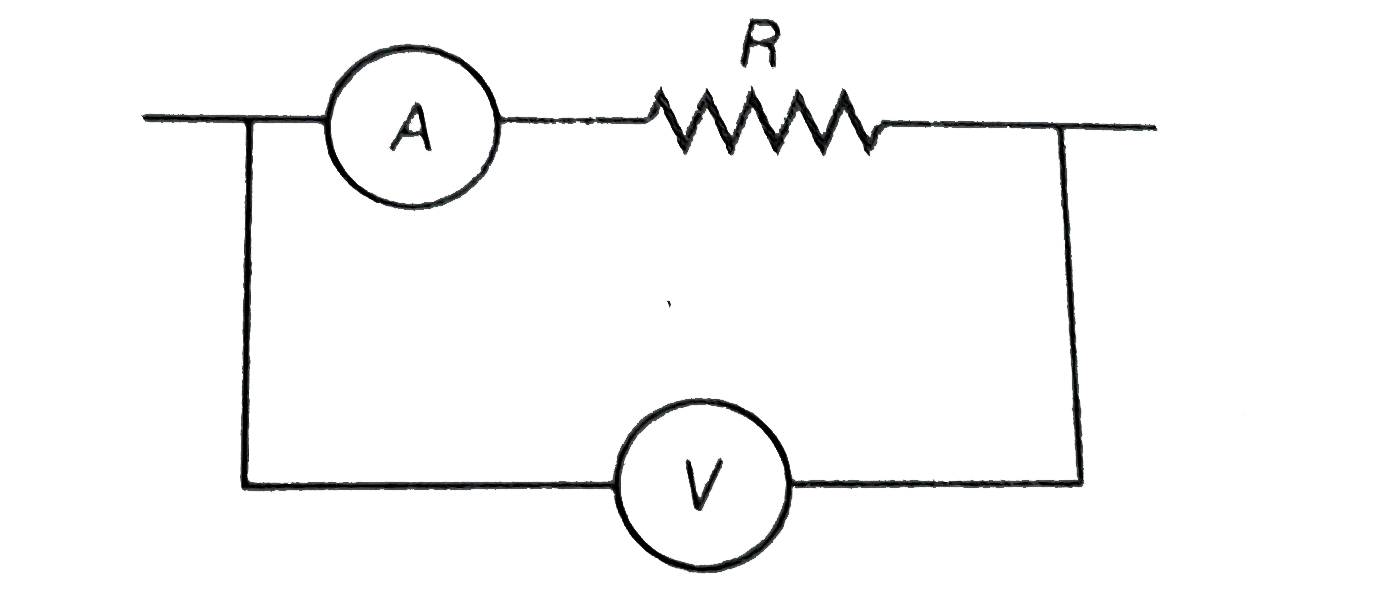
View SolutionIn the adjacent circuit the ammeter reads 5.0 A and voltmeter reads 20V. The value of resistance R is

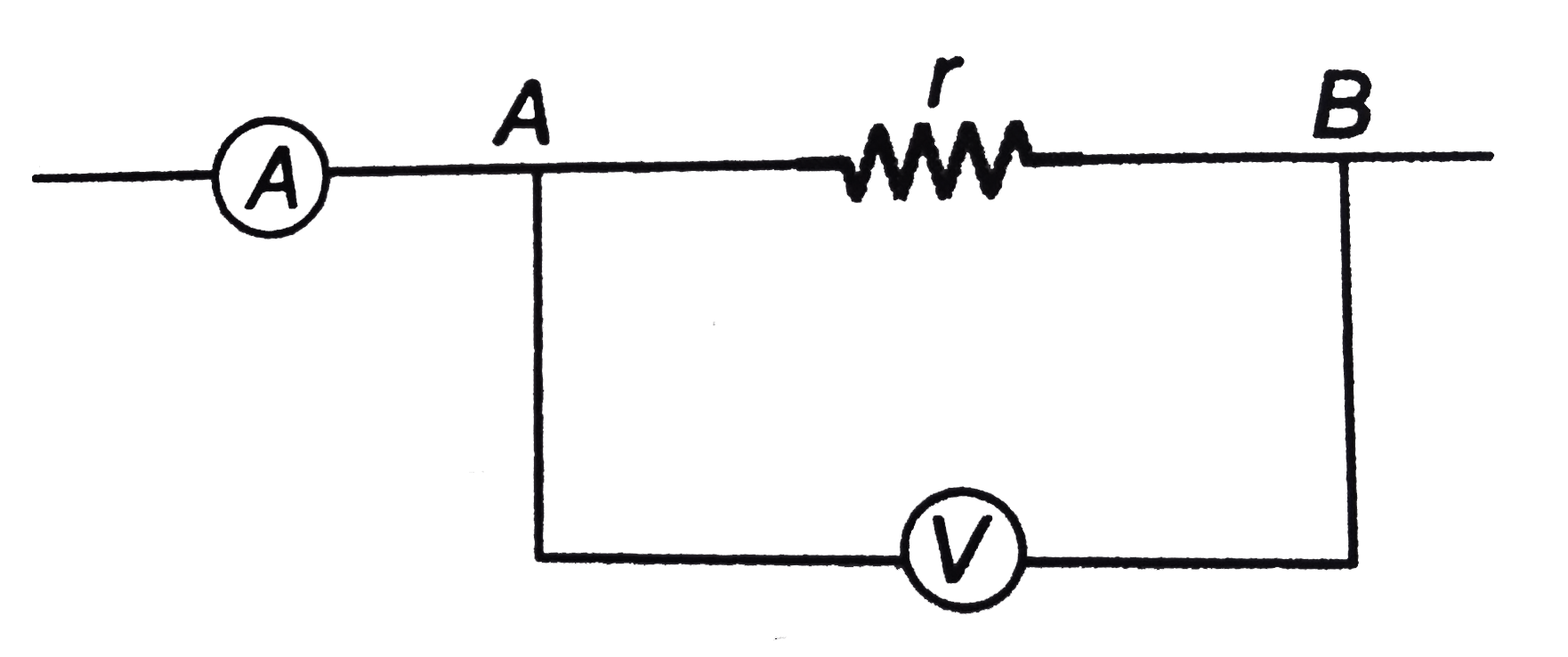
View SolutionDetermine the resistance r if an ammeter shows a current of I=5A and a voltmeter 100V. The internal resistance of the voltmeter is R=2,500Ω
View SolutionA 100 V voltmeter of internal resistance 20 kω is in series with a high resistance R, is connected to 110 V line . The voltmeter reads 5 V, then the value of R is
View Solution
