Two moving coil galvanometers 1 and 2 are with identical field magnets and suspension torque constants, but with coil of different number of turns N1 and N2, area per turn A1 and A2, and resistance R1 and R2. When they are connected in series in the same circuit, they show deflections θ1 and θ2. then θ1/θ2 is
A1N1/A2N2
A1N2/A2N1
A1R2N1/A2R2N2
A1R1N1/A2R2N2
The correct Answer is:A
I=kNBA6. Given that I1=I2
∴Kθ1N1BA1=Kθ2N2BA2
So θ1θ2=A1N1A2N2
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Multiple Correct
7 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Assertion-Reasoning
7 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Subjective
18 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
Similar Questions
Knowledge Check
Two ammeters, 1 and 2 have different internal resistances: r1 (known) and r2 (known). Each ammeter has scale such that the angular deviation of the needle for zero is proportional to the current passing through it. Initially, the ammeters are connected in series to a source of constant voltage. The deviations of the needles of the ammeter are θ1 and θ2, respecitively. The ammeters are then connected in parallel ot the same voltage source. This time, the deviations of the needles are θ'1 and θ'2 respectively. Find r2 in terms of r1,θ1,θ2,θ'1 and θ'2.
Ar1θ1θ'1θ2θ'2Br1θ2θ'1θ1θ'2Cr1θ2θ'2θ1θ'1Dr1θ2θ'2θ1θ'2If θ=π2n+1, then
cosθcos2θcos22θ…cos2n−1θ is equal toA12nBcosθC2D2nTwo different metal rods of the same length have their ends kept at the same temperature θ1, and θ2with θ2>θ1. If A1 and A2 are their cross-sectional areas and K1 and K2 their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
AA1A2=k1k2BA1A2=k2k1CA1A2=k1θ1k2θ2DA1A2=k2θ2k1θ1
Two tangent galvanometers have coils of the same radii, differing only in their number of turns. They are connected in series. When a steady current is passed in the circuit, the mean deflections in the galvanometer are θ1 and θ2. Deduce an expression for the ratio of number of turns of the galvanometer.
View SolutionThe sensitivity of a moving coil galvanometer can be increased by
(1) decreasing the couple per unit twist of the suspension
(2) increasing the number of turns in the coil
(3) decreasing the area of the coil
(4) decreasing the magnetic field
View Solution∞∑n=1tan(θ2n)2n−1cos(θ2n−1) is
View SolutionThree ammeters — 1, 2 and 3 have different internal resistances r1,r2andr3 respectively. Internal resistance r1 is known but r2andr3 are unknown. The angular deflection of pointer in each ammeter is proportional to the current. Initially, the three ammeters were connected in series to a voltage source (fig. a) and deflections for the three ammeters were θ1,θ2andθ3 respectively. The three ammeters were then connected in parallel to the same voltage source (fig. b). This time the deflections were observed to be θ'1,θ'2 and θ'3 respectively.
(a) Find r2andr3.
(b) If θ2=θ3 but θ'3>θ'2 then which one is larger r2orr3 ?
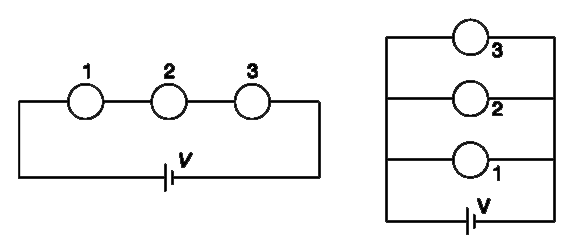
View Solutionprove that : tan2nθtanθ=(1+sec2θ)(1+sec22θ)(1+sec23θ)…(1+sec2nθ)
View Solution
