Two heater coils made of the same material are connected in parallel across the mains : the length and the diameter of one coil is double that of the other . Which of them will produce more heat?
According to Joule heating , the rate at which heat is produced in a resistance is given by P=I2R=V2/R. And in parallel , V is same , i.e, V1=V2 . So,
P2P1=R1R2=L1L2[r2r1]2 [asR=ρLπr2]
=L12L1[2r1r1]2 [asL2=2L1andr2=2r1]
or P2=2P1
That is heat produced in the thicker coil is more ( i.e, double) than that produced in the other coil.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective
8 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Single Correct
60 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Solved Examples
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Concept Based
9 Videos
Similar Questions
(a) Two heater coils made of the same material are connected in paralled across the mains. The length of diameter of one the coil is triple that of other. Which of these will produce more heat?
(b) Three equal resistors connected in series across a source of emf together dissipated 10Wa of power. What would be the power disspated if the same resistors are connected in parallel across the same source of emf?
Two resistor R1 and R2 may be connect either in series or in parellel across a battery of zero internal resistance. it is required that joule heating for the parallel combination be four times than for series combination. if R1=100Ω find R2
(d) The three resistance A,BandC have values 3R,6R and R respectively. Now some potential difference is applied across the network . Find the ratio of thermal powers dissipated between X and Y . find ratio of power consumed by A,B,andC.
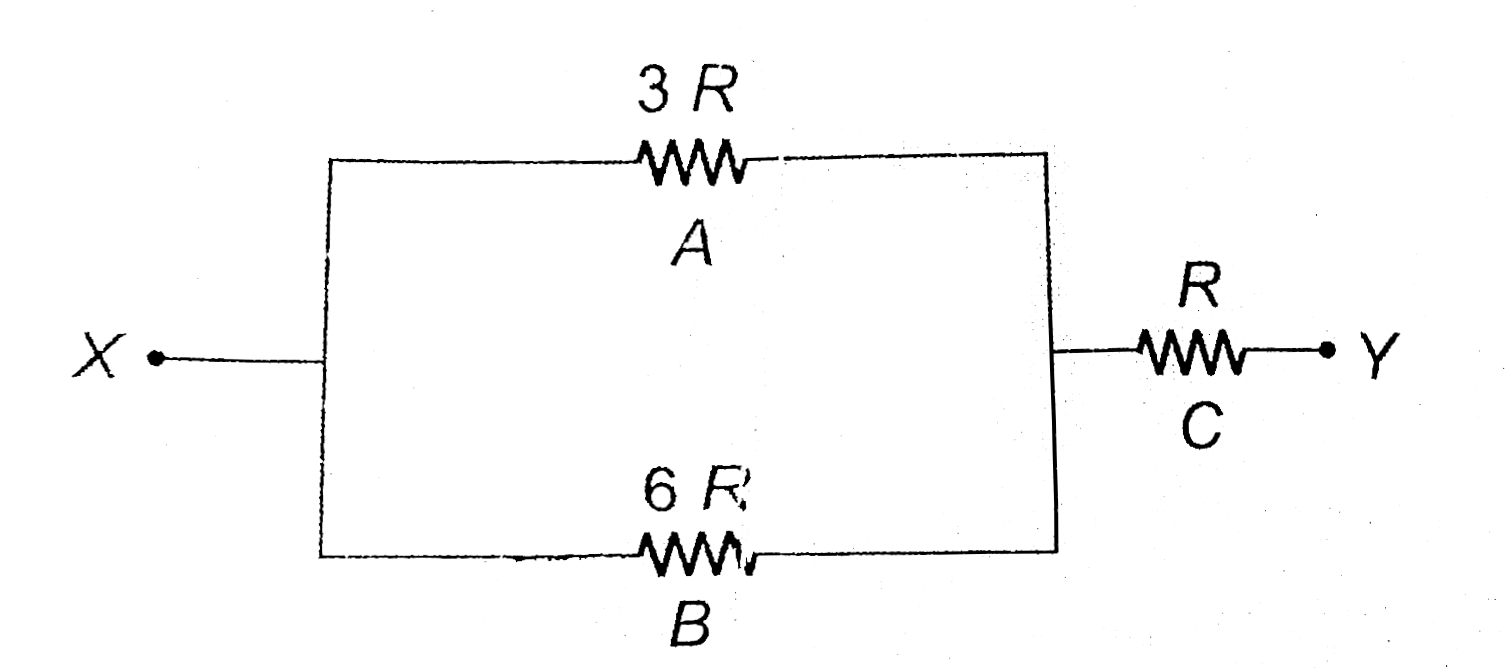
View SolutionTwo resistance wire "A" and "B" of same material are connected in parallel to the mains.The length and diameter of wire "A" are double those of wire "B" . The amounts of heat generated "Q_(A) and "Q_(B)" in "A" and "B" will be-
View Solution
Knowledge Check
Two concentric coils carry the same current in opposite directions. The diameter of the inner coil is equal currents. The outer coil. If the magnetic field produced by the outer coil at the common centre are 1T, the net field at the centre is
A1TB2TC3TD4TTwo identical coils each of self-inductance L , are connected in series and are placed so closed to each other that all the flux from one coil links with the other. The total self-inductance of the system is
ALB2LC3LD4LAn electric kettle has tow heating coils. When one of the coils connected to an AC source, the water in the kettle boils in 10 min. when the other coil is used the water boils in 40 min. if both the coils are connected in parallel, the time taken by the same quantity of water of boil will be
A25 minB15 minC8 minD4 min
Two pieces of conductor of same material and of equal length are connected in series with a cell. One of the two pieces has cross-sectional area double that of the other. Which one of the following statements is correct in this regard ?
View SolutionTwo heater wires, made of the same material and having the same length and the same radius, are first connected in series and then in parallel to a constant potential difference. If the rate of heat produced in the two cases are Hs and Hp respectively then HsHp will be
View SolutionTwo wires are of the same length, same radius, but one of them is of them is of copper and the other is of iron. Which will have more resistance ?
View SolutionTwo iron spheres of the same diameter are heated to the same temperature. One is soled, and the other is hollow which will expand more?
View SolutionTwo conducting wires of the same material and of equal length and equal diameters are first connected in series and then in parallel in an electric circuit. The ratio of the heat produced in series and parallel combinations would be :
View Solution