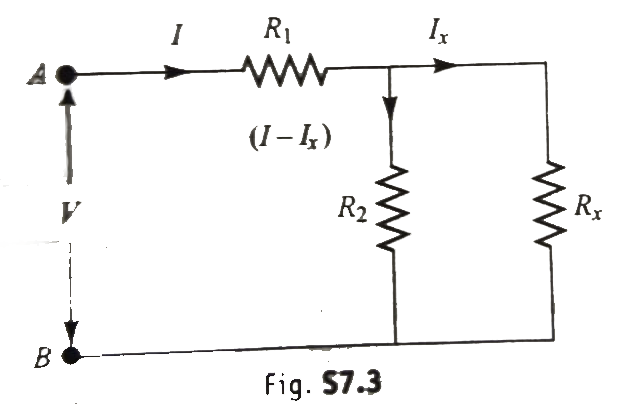
A circuit shown in the figure has resistances 20Ω and 30Ω. At what value of resistance Rx will the thermal power generated in it be practically independent of small variations of that resistance? The voltage between points A and B is supposed to be constant in this case.

The correct Answer is:12ω
The equivalent resistance between the points is
R0=R1+R2RxR2+Rx
Power generated by RxisI2xRx.
From fig. S7.3, I=⎛⎜⎝VR1+R2RxR2+Rx⎞⎟⎠
Ix=⎛⎜⎝VR1+R2RxR2+Rx⎞⎟⎠(R2R2+Rx)
Px=I2xRx=[VR2R1R2+R1Rx+R2Rx]2Rx
For the maximum value , dPxdRx=0
or R1R2+R1Rx+R2Rx=2(R1+R2)Rx
or Rx=R1R2R1+R2=20×3020+30=12Ω
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Single Correct
60 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Multiple Correct
5 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.1
22 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Concept Based
9 Videos
Similar Questions
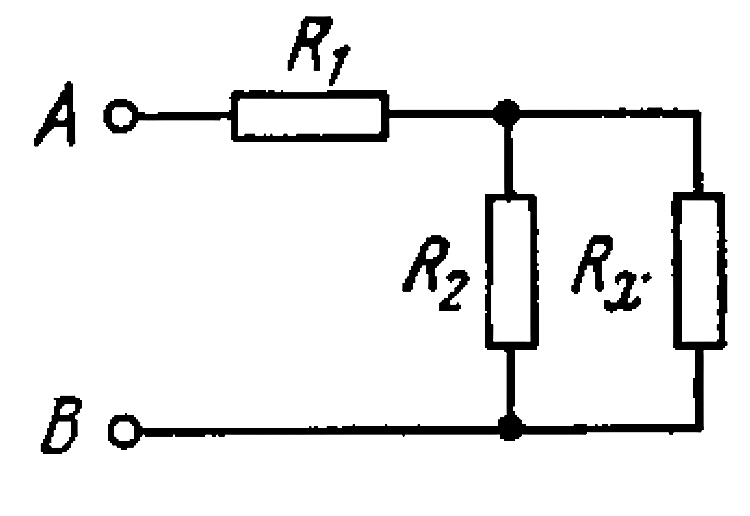
A circuit shown in Fig, has resistances R1=20Ω and R2=30Ω. At what value of the resitanace Rx will the thermal power generated in it practically independent of small variations of that resistance? The voltage between the points A and B is supposed to be constant in this case
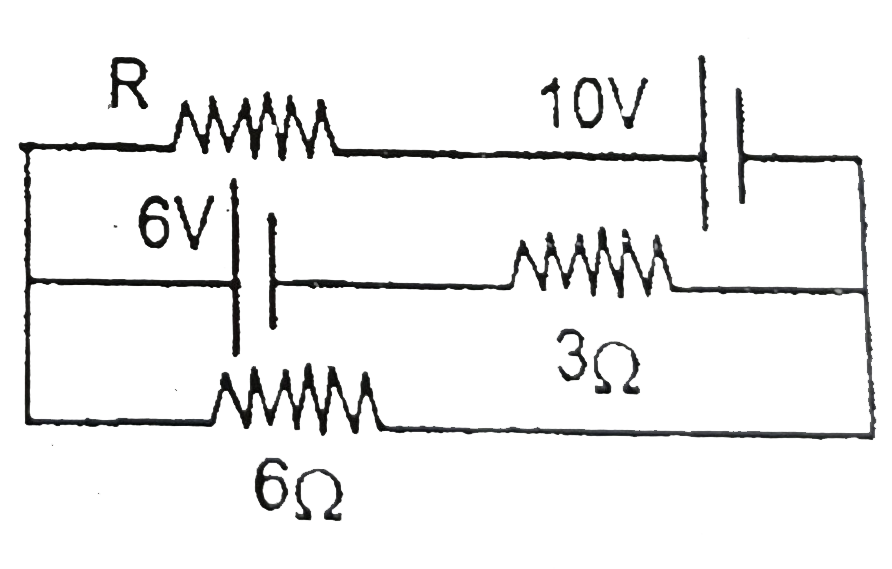
View SolutionIn a circuit shown in figure if the internal resistance of the sources are negligible then at what value of resistance R will the thermal power generated in it be the maximum. What is its value in ohms ?
View Solution
Knowledge Check
Consider the circuit shown in the figure. The value of the resistance X for which the thermal power generated in it is practically independent of small variation of its resistance is
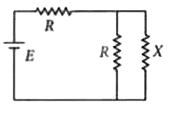 AX=RBX=R3CX=R2Dx=2R
AX=RBX=R3CX=R2Dx=2RIn the circuit shown in figure the total resistance between points A and B is R0. The value of resistance R is
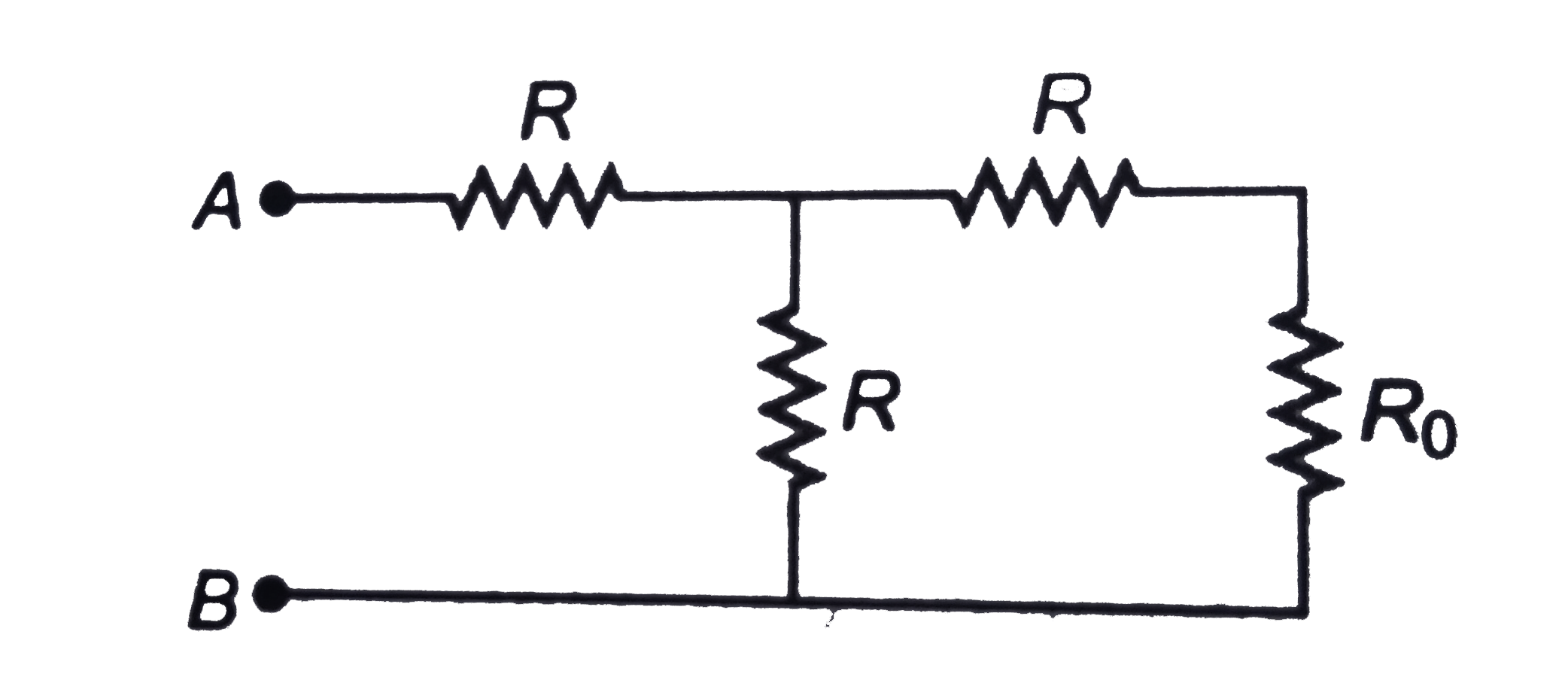 AR0B√3R0CR02DR0√3
AR0B√3R0CR02DR0√3In the circuit shown in the figure, the current flowing in 2Ω resistance
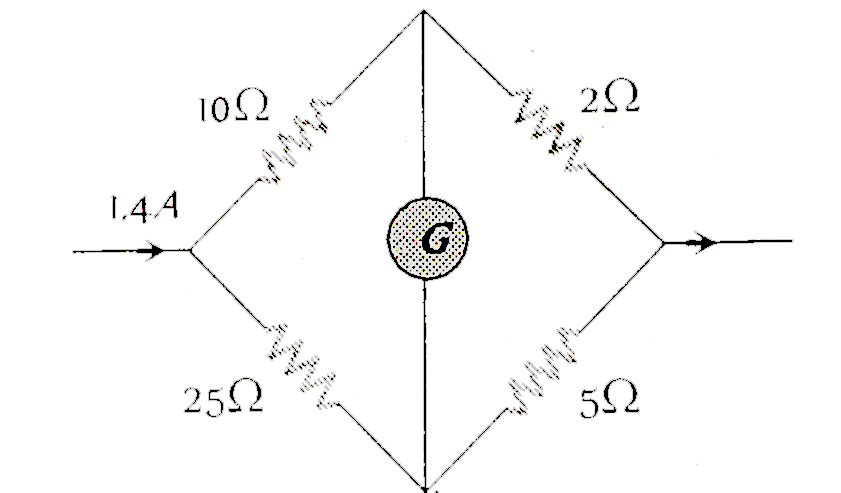 A1.4AB1.2AC0.4AD1.0A
A1.4AB1.2AC0.4AD1.0A
In a circuit shown in figure if the internal resistances of the sources are negligible then at what value of resistance R will the thermal power generated in it will be the maximum. What is the value of maximum power?
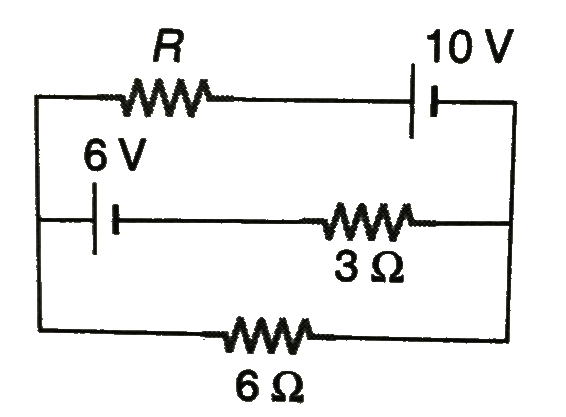
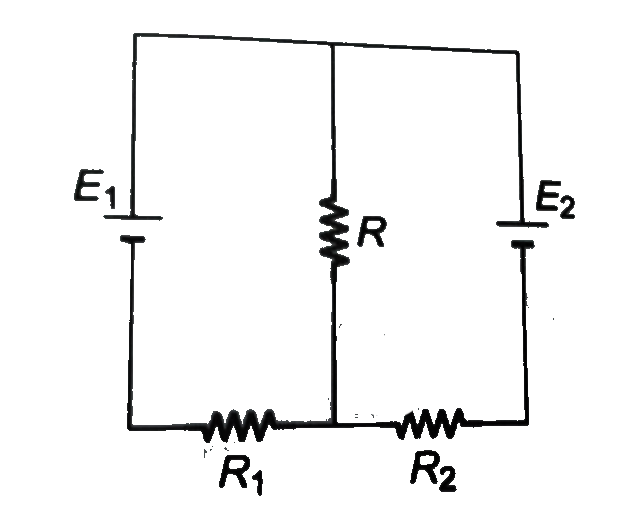
View SolutionIn the circuit shown in figure, the emfs of batteries are E1, and E2 which have internal resistances R1, and R2. At what value of the resistance R will the thermal power generated in it be the highest? What it is?
View SolutionIn the given circuit if the internal resistance of the batteries are negligible, then for what value of resistance R(inΩ) will the thermal power generated in it be maximum.

View SolutionIn the circuit shown in figure, power developed across 1Ω,2Ω and 3Ω resistance are in the ratio of
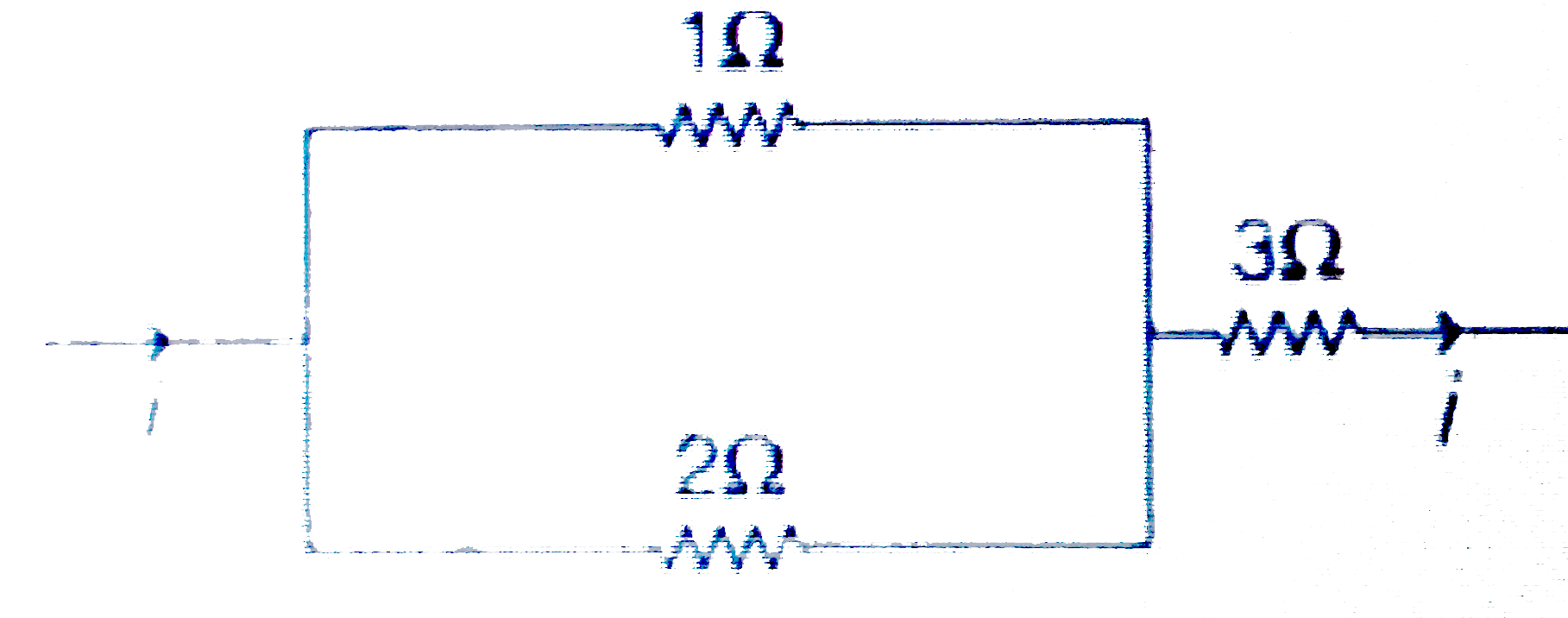
View SolutionIn the circuit shown in figure, each resistance is Net resistance between points A and B is

View Solution