In a experiment , N identical electrical bulbs, each having resistance R , are connecteed in parallel to a dc source of emf E and internalresistance r . What is the power consumed by each bulb . Also find the percentage change in power by each bulb if one bulb turns out.
The correct Answer is:E2R((Nr+R))2 , 200rNr+R
If R is the resistance of each bulb, then the equivalent resistance of N bulbs in parallel is Req=R/N. Therefore , current is equally divided among all the N bulbs, as potential drop across each bulb is the same. So power consumed by each bulb is
P=(iN)2R=E2N2(RN+r)2=E2R(Nr+R)2 (i)
With (N−1) bulbs, the power consumed by each bulb can be obtained by replacing Nby(N−1) in Eq. (i). So,
Now , percentage change in power consumption of each bulb is
P'−PP×100=(rN+R)2[(r(N−1)+R)]2−1]×100
=⎡⎢
⎢
⎢⎣1[(1−rNr+R)]2−1⎤⎥
⎥
⎥⎦×100
As r<<(Nr+R),(1−rNr+R)−2−1+2rNr+R
Therefore, percentage change in power is
2rNr+R×100=200r(Nr+R)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Single Correct60videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Multiple Correct5videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.122videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Concept Based9videos
INDUCTANCE
Similar Questions
Two bulbs when connected in parallel to a source take 100 W each. The total power consumed when they are connected in series with the same source is
View SolutionThree bulbs,each having a resistance of 180(Ω)are connected in parallel to an ideal battery of emf60V. Find the current delivered by the battery when (a)all the bulbs are switched on,(b)two of the bulbs are switched on and (c )only one bulb is switched on.
View Solution
Knowledge Check
- Question 1 - Select One
If electric bulbs having resistances in the ratio 2 : 3 are connected in parallel to a voltage sources of 220 V. The ratio of the power dissipated in them is
A2: 3B3 : 2C1 : 1D2: 5 - Question 2 - Select One
Two bulbs when connected in parallel to a source take 60 W each, the power consumed, when they are connected in series with the same source is
A15 WB30 WC60 WD120 W - Question 3 - Select One
Two electric bulbs whose resistances are in the ratio 1:3 are connected in parallel to a constant voltage source. The powers dissipated in them have the ratio
A1:3B1:1C3:1D1:9
Three identical bulbs are connected in parallel across an ideal sources of emf E .The ammeter A and voltmeter V are ideal . If bulb B3 gets fused, then
_PHY_E05_094_Q01.png) View Solution
View SolutionThree identical bulbs are connected in parallel across in ideal source of emf E. The ammeter A and voltmeter V are ideal. If bulb (B3) gets fused, then
_PHY_E05_042_Q01.png) View Solution
View SolutionTwo identical bulbs are conneted in parallel across an ideal source of emf E . The ammeter A voltmeter V are ideal . If bulb B2 gets fused , then
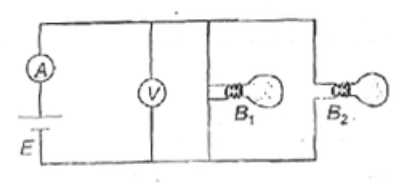 .View Solution
.View SolutionTwo electric bulbs whose resistance's are in the ratio 1 : 2 are connected in parallel to a constant voltage source . The power dissipated in them have the ratio
View SolutionTwo electric bulbs whose resistances are in the ratio of 1:2 are connected inparallel to a constant voltage source. The powers dissipated in them have the ratio
View Solution

