At a distance r from a point located at origin in space, the electric potential varies as $V = 10 r$ . Find the electric field at $\to r = 3 ˆ i + 4 ˆ j - 5 ˆ k$ .

$(\sqrt{2}) (3 ˆ i + 4 ˆ j - 5 ˆ k)$

$(- \sqrt{2}) (3 ˆ i + 4 ˆ j - 5 ˆ k)$

$(- \sqrt{3}) (3 ˆ i + 4 ˆ j - 5 ˆ k)$

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Let $V_{0}$ be the potential at the origin in an electric field $\to E = 4 ˆ i + 5 ˆ j$ . The potential at the point (x,y) is
A $V_{0} - 4 x - 5 y$
B $V_{0} + 4 x + 5 y$
C $4 x + 5 y - V_{0}$
D $- 4 x - 5 y$
The variation of potential with distance R from the fixed point is shown in (Fig. 3.125).
.
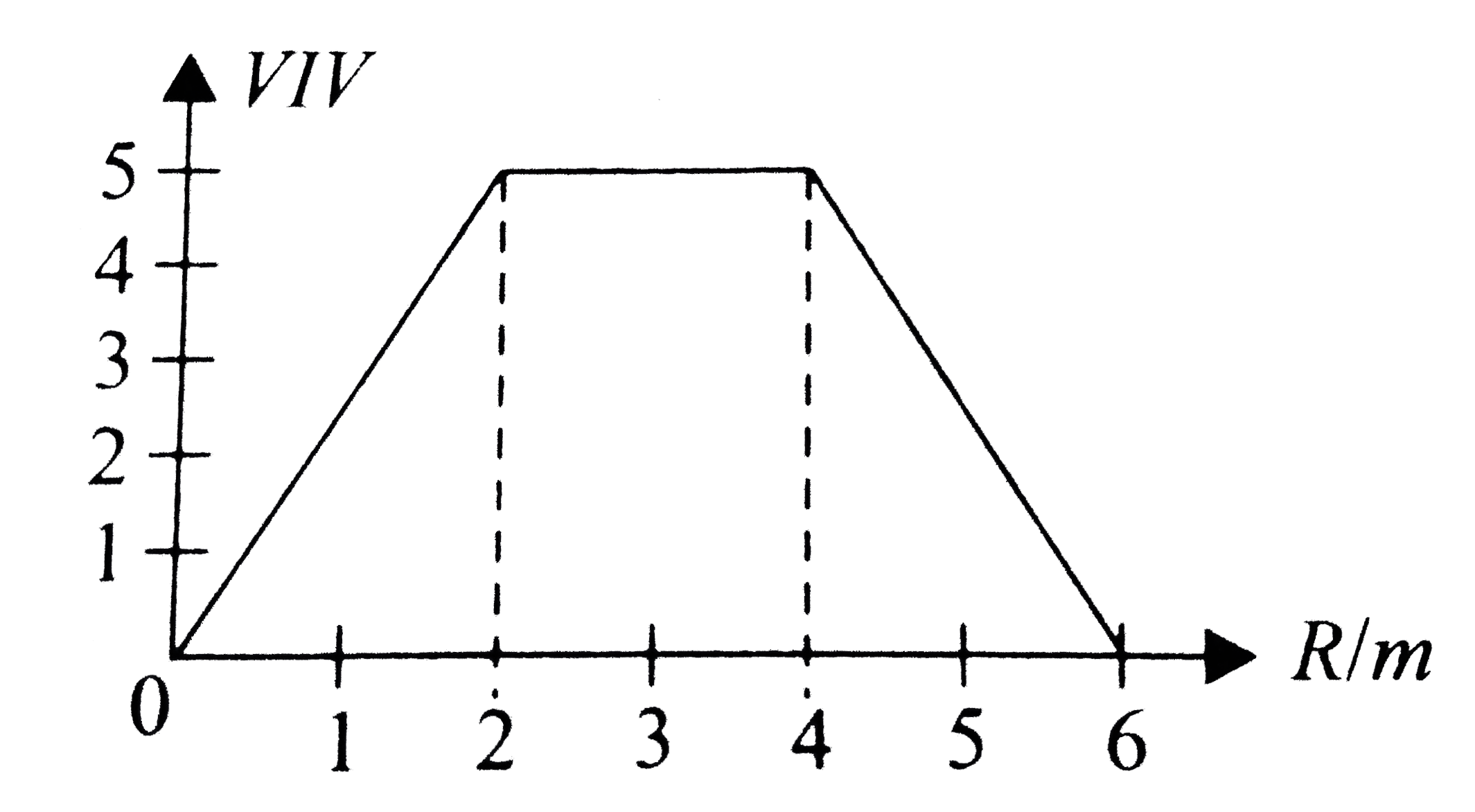The electric field at $R = 5 m$ is.
A $2.5 V m^{- 1}$
B $- 2.5 V m^{- 1}$
C $0.4 V m^{- 1}$
D $- 0.4 V m^{- 1}$
The electric field and the potential of an electric dipole vary with distance r as
A $\frac{1}{r}$ and $\frac{1}{r^{2}}$
B $\frac{1}{r^{2}}$ and $\frac{1}{r}$
C $\frac{1}{r^{2}}$ and $\frac{1}{r^{3}}$
D $\frac{1}{r^{3}}$ and $\frac{1}{r^{2}}$