In the given electric field →E=[α(d+x)ˆi+E0ˆj]NC−1, where α=1NC−1 hypothetical closed surface is taken as shown in figure .
![In the given electric field vecE = [alpha(d+x)hati + E0hatj] NC^(-1), where alpha = 1NC^(-1) hypothetical closed surface is taken as shown in figure . The total charge enclosed within the close surface is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V03_CA1_E01_042_Q01.png)
The total charge enclosed within the close surface is
abcε02
acdε02
abdε02
none of these
The correct Answer is:A
a. ϕABCD=−acd unit
ϕCDEF=−beE0 unit
ϕABEF=bcE0+c∫a0(d+x)dy
=+bcE0+acd+c∫boxdx
[Since xb+ya=1 or dxb=−dya]
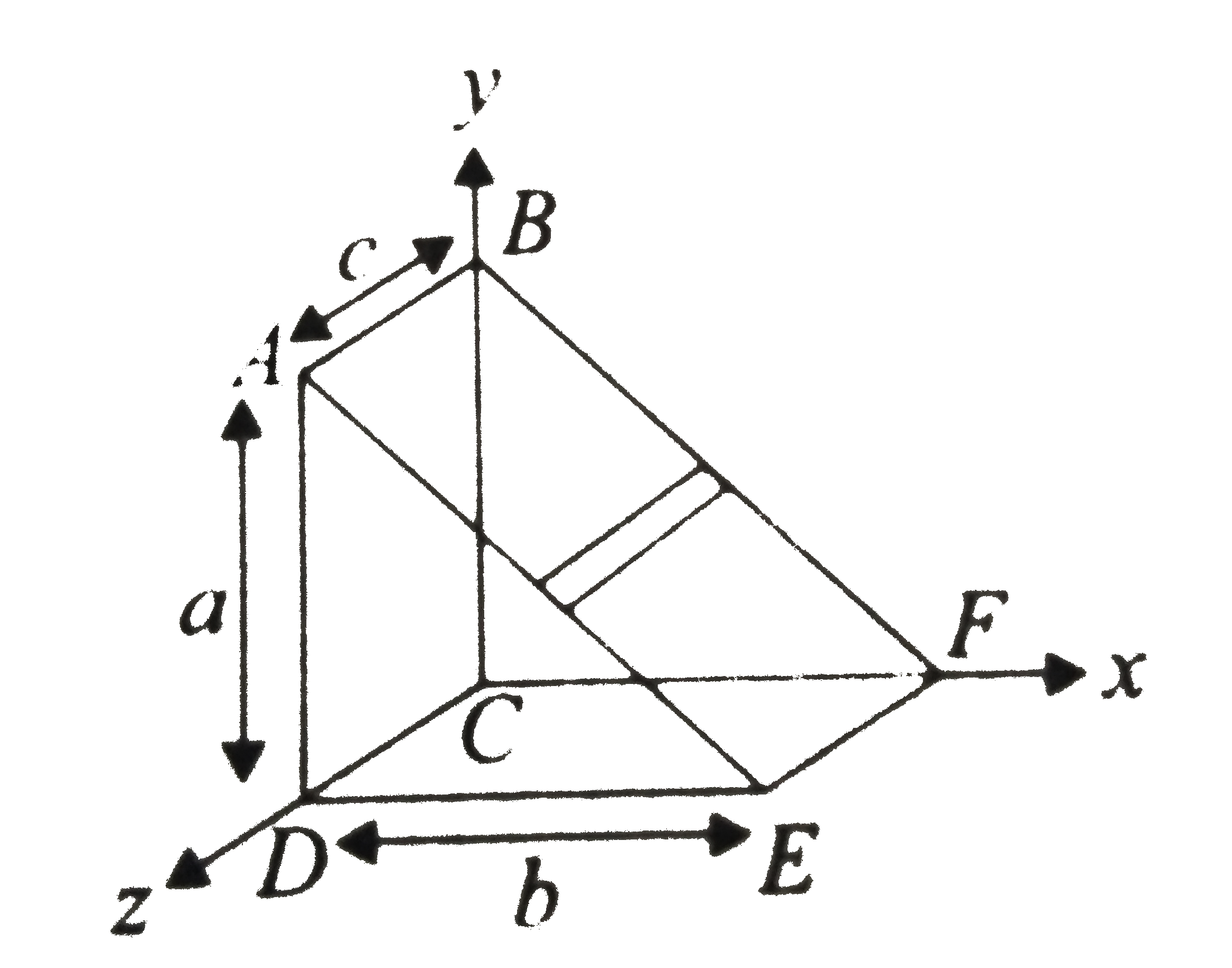
=[+bcE0+acd+acb2] unit
Using Gauss's law, we get
ϕset=qinε0 or qin=abcε02
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type
109 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
In the given electric field →E=[(d+x)ˆi+E0ˆj]N/Ca hypothetical closed surface is taken as shown in figure. The total charge enclosed within the closed surface is Kε0. Then, find the value of k. (a=2m, b=3m and c=2m)
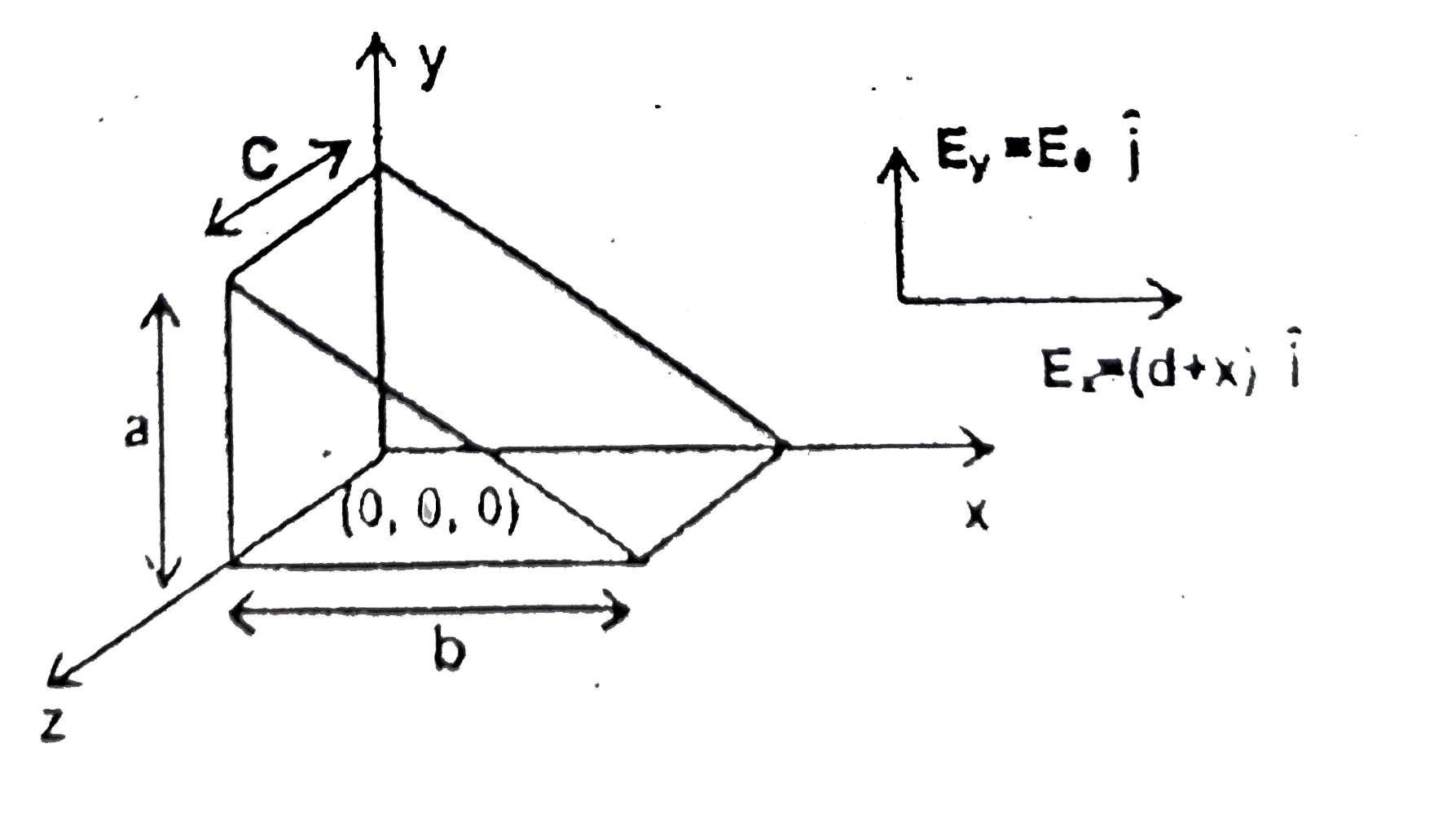
View SolutionFind the flux of the electric field through each of the five surfaces of the inclined plane as shown in figure. What is the total flux through the entire closed surface?

View Solution
Knowledge Check
The number of electric lines of forces rediating from a closed surface in vacumm is 1.13×1011. The charge enclosed by the surface is
A1CB1μCC0.1CD0.1μCIn a negion the intensity of an electric field is given by E=Sˆi+8ˆj+ˆk in NC−1. The electric flux a surface
S=10ˆim2 in the region isA10Nm2C−3B80Nm2C−3CNm2C−3DNoneAssume that an electric field →E=40x3ˆiNC−1 exists in space. The charge density at x=2m is:
A360ε0, Coulmb m−3B120ε0 Coulmb m−3C240ε0, Coulmb m−3D480ε0, Coulmb m−3
Find the flux of the electric field through each of the five surfaces of the inclined plane as shown in figure. What is the total flux through the entire closed surface?

View SolutionIf the electric flux entering and leaving a closed surface in air are ϕ1andϕ2 respectively, the net electric charge enclosed within the surface is ____________ .
View SolutionA closed surface encloses a net charge of −3.60μC. What is the net electric flux through the surface?
(b) The electric flux through a closed surface is found to be 780N−m2/C. What quantity of charge is enclosed by the surface?
(c) The closed surface in part (b) is a cube with sides of length 2.50 cm. From the information given in part (b), is it possible to tell where within the cube the charge is located? Explain.
View SolutionA closed surface encloses a net charge of −3.60μC. What is the net electric flux through the surface?
(b) The electric flux through a closed surface is found to be 780N−m2/C. What quantity of charge is enclosed by the surface?
(c) The closed surface in part (b) is a cube with sides of length 2.50 cm. From the information given in part (b), is it possible to tell where within the cube the charge is located? Explain.
View SolutionIf the electric flux entering and leaving an enclosed surface are ϕ1andϕ2 respectively, then the electric charge present within the surface is
View Solution
