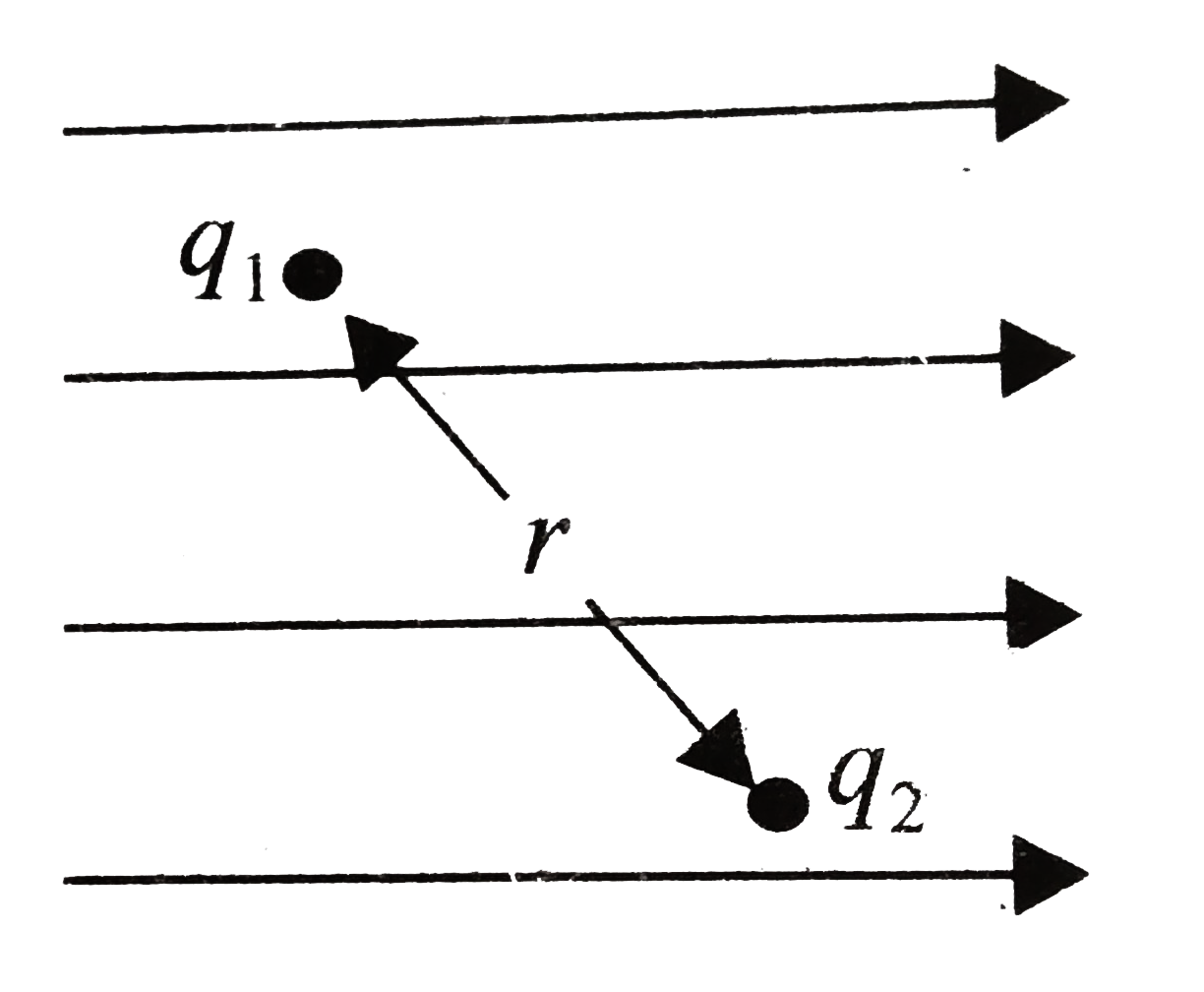
Two point charges q1andq2 are placed in an external uniform electric field as shown in figure. The potential at the location of q1andq2 are V1andV2, i.e., V1andV2 are potentials at location of q1andq2 due to external unspecified charges only. Then electric potential energy for this configuration of two charged particle is
q1V1+q2V22
q1V1+q2V2
q1V1+q2V2+q1q24πε0r
q1q24πε0r
The correct Answer is:C
The potential energy of the system can be found by computing the work done by enternal agent in assembling the system without changing the kinetic energy of the system. Let us first bring q1 from infinity to the desired location, then in doing so we have to do work against enternal electric field which is equal to W1=q1V1 (potential at infinity is considered as zero). Now, we will bring q2 from infinity to the desired location, to do so, we have to do work against external electric field and against electric force of q1, so work done is
W2=q2V2+q1q24πε0r
So total work done is U,
q1V1=q2V2+q1q24πε0r
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type
109 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Knowledge Check
Two points charges q and -2q are placed some distance d apart. If the electric field at the location of q is E, that at the location of -2q is
A−E2B−2ECE2D−4ETwo point charge qA and qB are placed in a uniform external electric field →E at point A and B respectively. The position vector of A is →rA and that of B is →rB. if V(→rA) and V(→rB) be the electric potentials at point A and B due to the external electric field →E, then potential energy of the system will be
AqAV(→rA)+qBV(→rB)BqBV(→rA)+qAV(→rB)CqAV(→rA)+qBV(→rB)+qAqB4πε0|→rAB|DqBV(→rA)+qAV(→rB)+qAqB4πε0|→rAB|The point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
A−3E2B−EC−E2D−2E
The point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
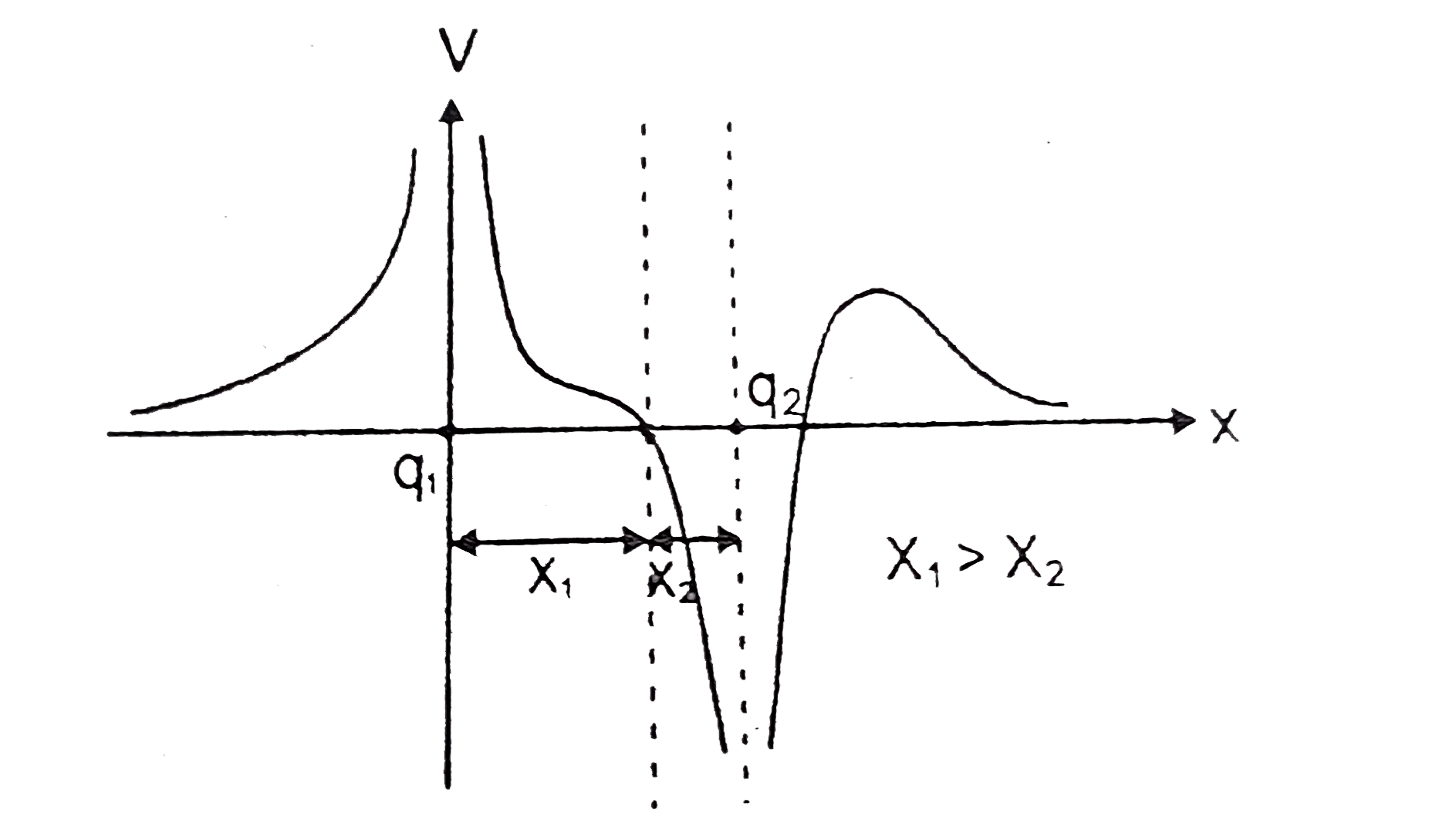
View SolutionTwo charge +q1 and +q2 placed on x-axis at posiution A and B as shown in figure. Which graph best represent potential as a function of distance r from charge q1

View Solution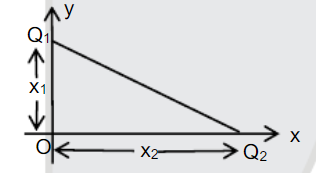
Two charge Q1 and Q2 are placed in xy plane at a distance x1 and x2 from origin a shown in figure. if electric field at O is same for both charge then find ratio Q1 and Q2.
View SolutionTwo charge +q1 and +q2 placed on x-axis at posiution A and B as shown in figure. Which graph best represent potential as a function of distance r from charge q1

View SolutionThe potential energy of a charged conductor of charge (q) and potential (v) is given by
View Solution