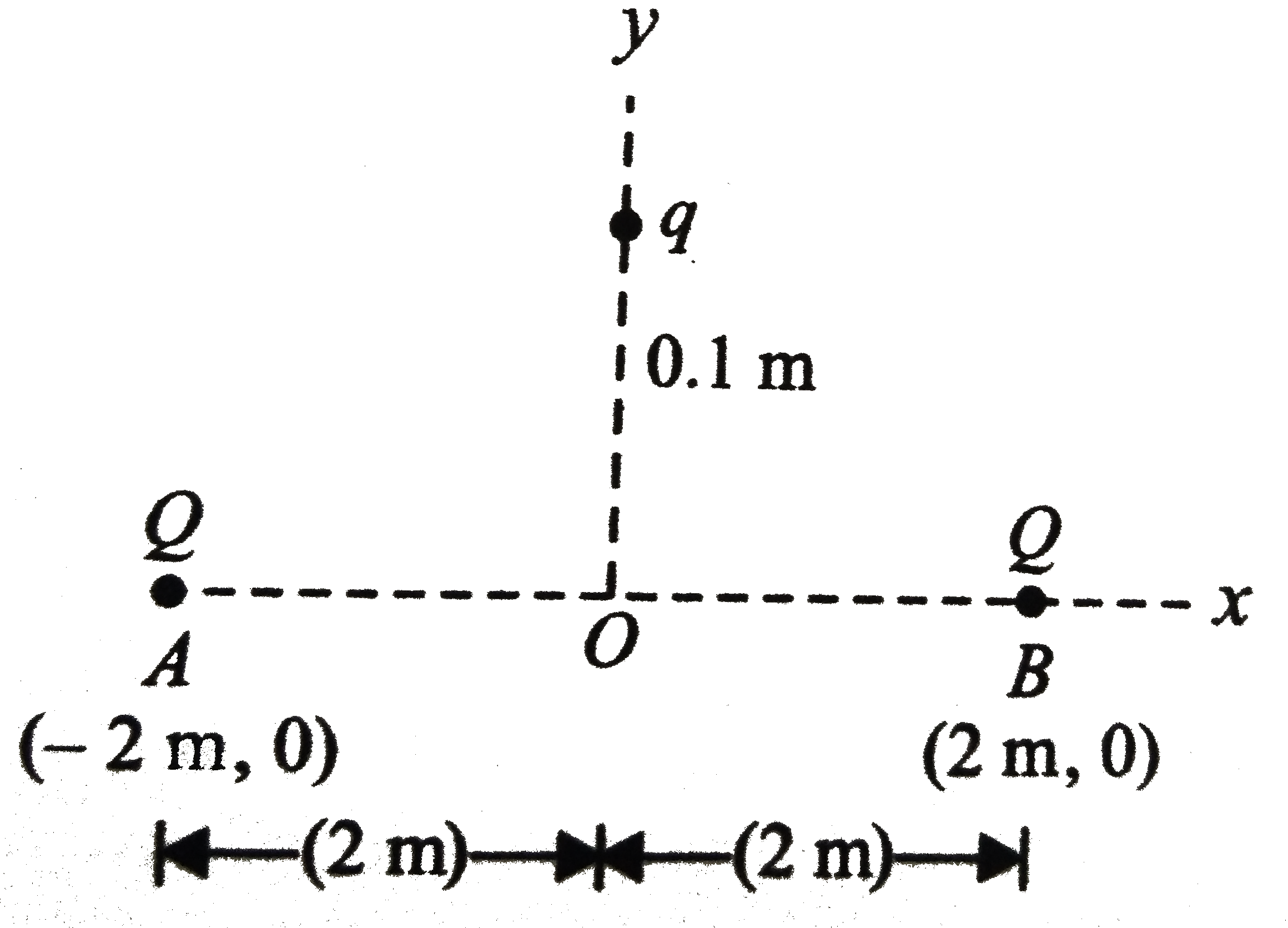
Consider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Equation of SHM (displacement from mean position) can be expressed as
y=0.1sin(10πt)
y=0.1sin(10πt+π/2)
y=0.1sin(5πt+π/2)
y=0.2sin(5πt)
The correct Answer is:B
Since Q8μC , if q is a positive charge, resultant force on it due to Q at A and Q at B will be along positive y−axis and it would move away along y−axix. But the charge q here is observed to oscillate. This is possible only if q is a negative charge so that resultant force on it is possible only if q is a negative charge so that resultant force on it is possible only if q is a negative charge so that resultant force on it due to Q at A and Q at B is towar O. Under the action of this force, q moves toward O, crsosses O and as it is moving along negative Y direction, resultant force on it will again be toward O. This force retards the motion of q along negative y−axos. It comes to rest at some point and then moves back toward O and so on (Fig.SA1.77). Force applied by Q on q has a magnitude
F=14πε0QqY2+a2
Force applied by Q at A on q can be resolved into rectangular components: Fωsθ and Fsinθ. Similarly, force applied by Q at B on q can be resolved into components: Fcosθ and Fsinθ.Fsinθ components of the two forces balance each other so that the net force on q is 2Fcosθ toward O. Therefore, net force on q.
Fn=214πε0Qqy2+a2cosθ
Fn=14πε02Qqy2+a2y(y2+a2)1/2=14πε02Qqy(y2+a2)3/2 ..(i)
for y<<a net force on q,
Fn=14πε02Qqya3 ..(ii)
Here Q=8μC=8×10−6C
At t=0, q is at y=0.1 m obviously y<a(=2m) since the motion is simple harmonic we can use the approximation y<≤a so initially i.e, at y=0 m force on q is 9×10−3 N
Units Eq. (i) we get
or 9×10−3=(9×109)2(8×10−6)q(0.1)(2)3
or q=5×10−6C=5μC
this, in fact, is the magnitude of q. We know that q, as explained earlier is a negative charge hence q=−5μC So correct option is (c).
At t=0 q is released at a piont 0.1 m from O on y-axis as it oscillates its other extreme position will be 0.1 m from O on the netative y-axis assuming undamped simple harmonic motion.
Hence amplitude of oscillation is 0.1 m or 10 cm so correct option is (a). from fig we get
Fn=14πε02Qqya3=ky ltbr where k=14πε02Qqa3
Thus, Fn∝y we also know that Fn always acts towards O (mean position) time period of resulting SHM will be T=2π√m/k of frequency is 12π√k/m
f=12π√14πε02Qqma3
=1(2×3.14)
⎷(9×109)(2)(8×10−6)(5×10−6)(91×10−6)(2)3=5
[m=91mg=91×10−6kg]
thus the correct option is (c).
In SHM, equation of displacement from mean position can be expressed as y=asin(ωt+ϕ) here a=0.1μ,ω=2πf=2π×5=10π,
y=0.1sin(10πt+ϕ)
but at t=0,y=0.1 Hence 0.1=0.1sinϕ or sinϕ=1
or ϕ=π2,y=0.1sin(10πt+π/2)
thus the correct option is (b). 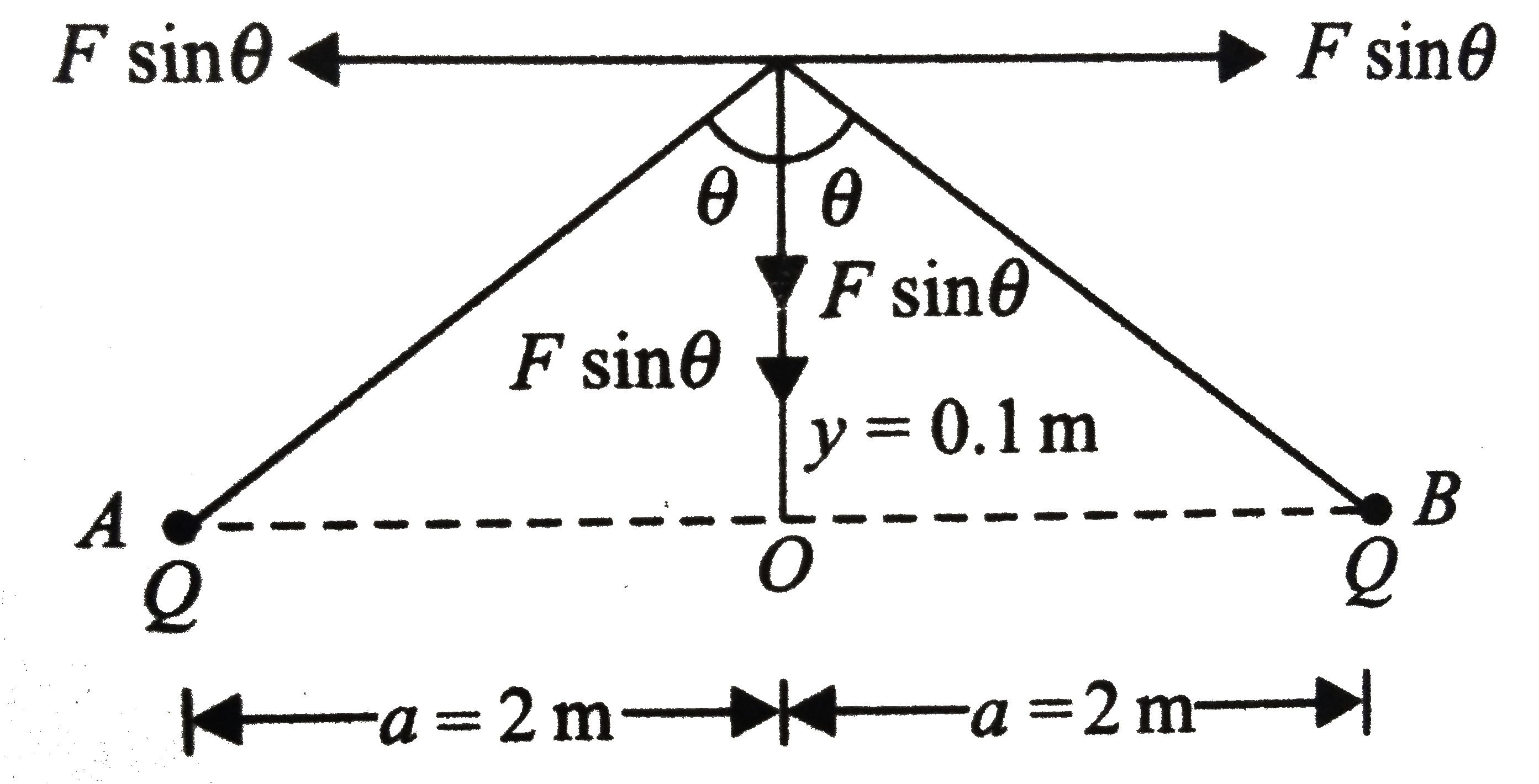
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Interger Answer type
20 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Consider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Charge q is
View SolutionConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Amplitude of motion is
View Solution
Knowledge Check
Consider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Charge q isA−8μCB−6.5μCC−5μCD+6.5μCConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Amplitude of motion isA10cmB20cmC30cmD40cmConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Frequency of oscillation isA8B10C5D2
Consider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Frequency of oscillation is
View SolutionTwo equal positive charges Q are fixed at points (a, 0) and (−a,0) on the x-axis. An opposite charge -q at rest is relased from point (0, a) on the y-axis. The charge -q will
View SolutionTwo equal negative charges −q are fixed at points (0,−a) and (0,a) on y-axis. A poistive charge Q is released from rest at point (2a,0) on the x-axis. The charge Q will
View SolutionTwo equal positive charges Q are fixed at points (a, 0) and (−a,0) on the x-axis. An opposite charge -q at rest is relased from point (0, a) on the y-axis. The charge -q will
View SolutionTwo equal negative charges −q are fixed at points (0,−a) and (0,a) on y-axis. A poistive charge Q is released from rest at point (2a,0) on the x-axis. The charge Q will
View Solution
