Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity σ and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
4πσln(b/a)V
4πσb/aV
2πσln(b/a)V
2πσb+aV
The correct Answer is:C
c. E=λ/2πε0r', where λ is the linear charge density of the inner
cylinder.
And V=∫baEdl=λ2πε0In(ba)
Now, I=∫→J.d→A=σ∫→E⋅d→A
=σ∫(λ2πε0r)2πrdr
Current per unit length will be
I=σλε0
From Eq. (i), we get
I=2σπε0ε0In(b/a)v=2πσIn(b/a)v
Alternatively,
I=VRorR=∫bx=a(iσ)dx2πx1=12πrIn(ba)
∴I=2πσVIn(b/a) .
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider a thick cylinder of inner radius a and b has conductivity σ. A battery of emf V is connected between the inner and outer surface of the cyllinder. Find the current flowing, per unit length of the cylinder
A4πσln(b/a)VB4πσ(b+a)VC2πσ(b+a)VD2πσln(b/a)V - Question 2 - Select One
There is one long non-conducting solid cylinder of radius R. The volume charge density is given by ρ=kx2 where k is a constant and x is the distance of the point from centre of cylinder. Electric field intensity inside the cylinder at a distance x from the centre is
Akx23ε0Bkx34ε0Ckx32ε0Dkx3ε0
A hollow cylinder of length l and of radii a and b is filled with a material of resistivity ρ and is connected to a battery of emf E through an ammeter. Find the current through ammeter
 View Solution
View SolutionConsider a hollow cylinder of length L and inner radius a and outer radius b, as shown in figure. The material has resistivity ρ.
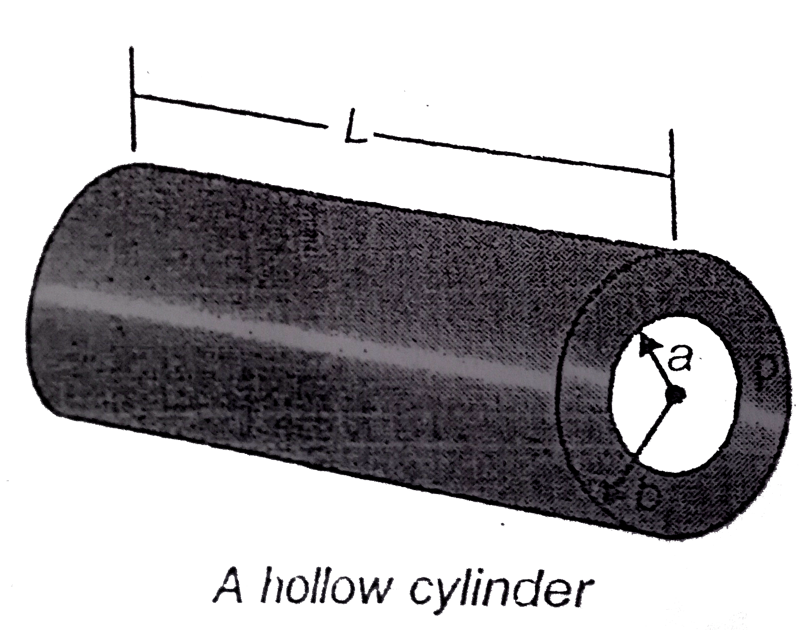
(a) Suppose a potential difference is applied between te ends of the cylinder and produces a current parallel to the axis. What is the resistance measure ?
(b) If instead the potential difference is applied between the inner outer surfaces so that current flows radially outward, what is the resistance measure ?View SolutionFind the force per unit area on the surface of a long hollow cylinder carrying uniform current I and radius of the cylinder is R.
View SolutionFind the force per unit area on the surface of a long hollow cylinder carrying uniform current I and radius of the cylinder is R.
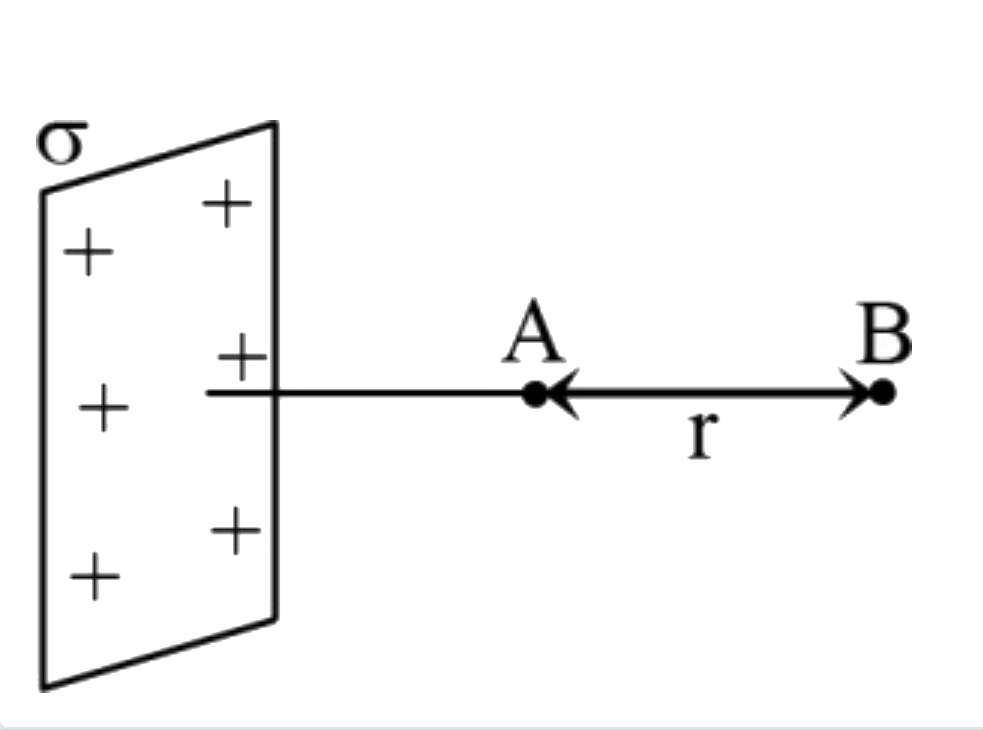
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
 View Solution
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
 View Solution
View Solution

