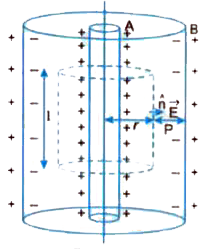
A long charged cylinder of linear charged density à is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
Let A be a long charged cylinder of linear charge density ^ and B be a hollow co-axial conducting cylinder. Charges are induced on B as shown in Fig. 2.08. Let us find electric field at a point P in the space between the two cylinders situated at a distance r from axis of cylinders.
To find at point P consider a cylinder of length land radius r as the Gaussian surface. Obviously total electric flux over the surface
According to Gauss.s theorem, the electric flux
(charged enclosed) ...(ii)
Comparing the values of electric flux given by (i) and (ii), we have
Obviously, the electric field is radial i.e., field is directed outward perpendicular to the charged cylinder.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - MULTIPLE CHOICE QUESTIONS
35 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
A long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View SolutionA long charged cylinder of linear charge density λ surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?
View Solution
Knowledge Check
A very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
Aλ=RσBλ=−RσCλ=2πRσDλ=−2πRσ
A long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View SolutionA long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cyclinder. What is the electric field in the space between the two cylinders ?
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformaly charged line charge( linear charge density λ) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
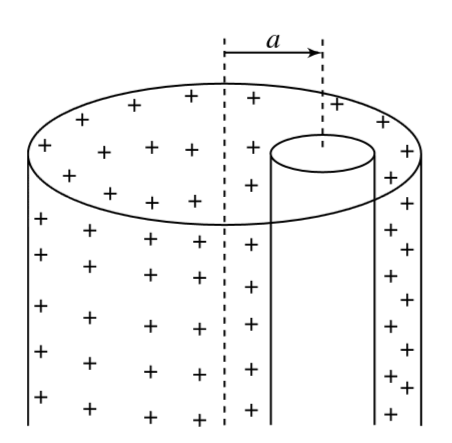
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
View SolutionA long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
View SolutionA dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density ρ varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that ρ is zero at the axis and it is equal to ρ on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [ρr23∈0a,ρa29∈0]
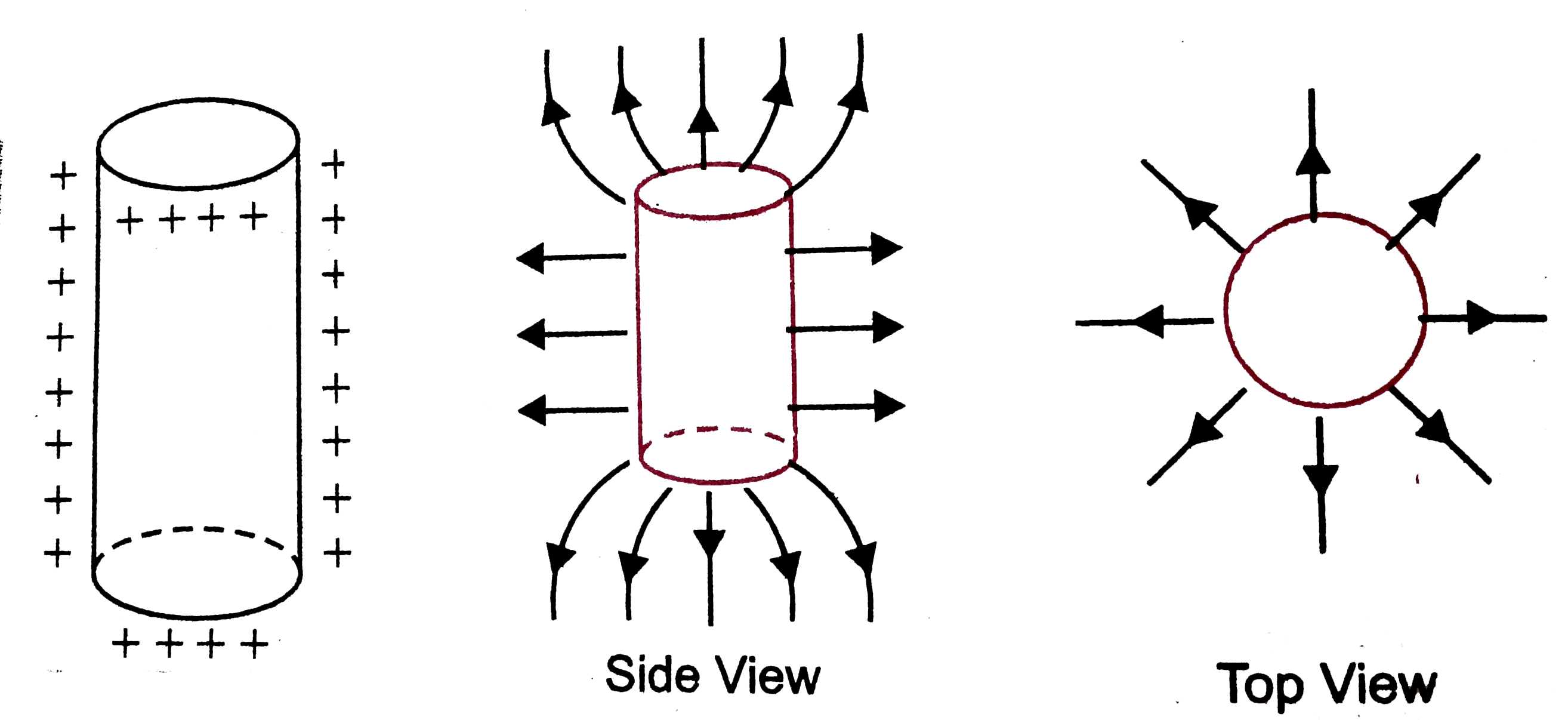
View SolutionSketch the electric field lines for a unifomly charged hollow cylinder shown in Fig.
View Solution
